Осцилляторным интегральным оператором называется оператор следующего вида:
![]() (1)
(1)
где ![]() и
и ![]() вещественно значная функция и
вещественно значная функция и ![]() — большой вещественный параметр.
— большой вещественный параметр.
В работе Л. Хёрмандера [4] доказано, что если смешенный Гессиан фазовой функции ф, т. е. ![]() , то для оператора (1) справедлива следующая оценка:
, то для оператора (1) справедлива следующая оценка:
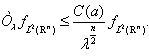 (2)
(2)
Однако, если смешенный Гессиан обращается в нуль в начале координат, то оценка (2) перестает быть справедливой.
В 1997 году в работе [5] И. М. Стейн и Д. Х. Фонг рассмотрели оценку норму оператора (1) с вырожденной фазой в случае ![]() . В этом случае по фазовой функции определяется так называемый приведённый многогранник Ньютона (МН), т. е. МН функции:
. В этом случае по фазовой функции определяется так называемый приведённый многогранник Ньютона (МН), т. е. МН функции: ![]() , предполагая
, предполагая ![]() .
.
Через d обозначается расстояние Ньютона, т. е координата пересечения биссектрисы положительного октанта с границей ![]() . Тогда если ф (х, у) аналитична в нуле и носитель амплитуды, а находится в достаточно малой окрестности нуля, то справедлива оценка:
. Тогда если ф (х, у) аналитична в нуле и носитель амплитуды, а находится в достаточно малой окрестности нуля, то справедлива оценка:
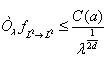 .
.
Более того, если ![]() , то существует ненулевая константа
, то существует ненулевая константа ![]() такая, что
такая, что 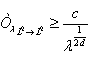 .
.
В дальнейшем, ради удобства введем обозначение: если существуют ненулевые константы
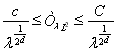 , то мы будем писать, что:
, то мы будем писать, что:
![]() (3)
(3)
Таким образом, если ![]() и носитель амплитуды находится в достаточно малой окрестности нуля, то справедливо соотношение (3).
и носитель амплитуды находится в достаточно малой окрестности нуля, то справедливо соотношение (3).
Основным результатом нашей работы является следующая теорема:
Теорема. Если ![]() и
и ![]() — носитель амплитуды находится в достаточно малой окрестности начала координат, то для L2 нормы осцилляторных интегральных операторов справедлива следующая оценка:
— носитель амплитуды находится в достаточно малой окрестности начала координат, то для L2 нормы осцилляторных интегральных операторов справедлива следующая оценка:
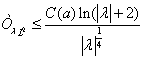 .
.
Более, того если ![]() , то при
, то при ![]() справедливо соотношение:
справедливо соотношение:
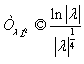 .
.
При доказательстве основной теоремы используются некоторые вспомогательные утверждения.
![]() метод и Обобщенная лемма Шура.
метод и Обобщенная лемма Шура.
Как известно, если Т некоторый ограниченный оператор в гильбертовом пространстве, то справедливо равенство ![]() .
.
Доказательство основной теоремы основывается на этом методе.
Лемма 1. ![]() является интегральным оператором с ядром:
является интегральным оператором с ядром:
![]()
Лемма 1 доказывается непосредственным вычислением ядро оператора![]() .
.
Лемма 2. Пусть М любое фиксированное число и ![]() тогда справедливо неравенство:
тогда справедливо неравенство:
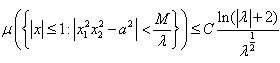
где ![]() Лебегова мера множества А.
Лебегова мера множества А.
Литература:
- Арнольд В. И., Варченко А. Н. Гусейн-заде С. М. Особенности дифференцируемых отображений. Ч. II. M.: Наука, 1984. 335 с.
- Варченко А. Н. Многогранники Ньютона и оценки осциллирующих интегралов. Функц. анал. и его прил. 10(3): (1976). с. 13–38.
- Рисс Ф. Б., Сёкефальви-Надь «Лекции по функциональному анализу». «МИР» Москва, 1979. 528 с.
- Хёрмандер Л. Анализ линейных дифференциальных операторов с частными производными. Ч. 4. ИнтегральныеоператорыФурье. М.: Мир, 1988. 446 с.
- Phong D. H., Stein E. M. The Newton polyhedron and oscillatory integral operators. Acta Math. 179(1) (1997), С. 105–152.







