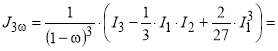Учет поврежденности монолитных и дискретных материалов при проектировании дорожных конструкций



Учет поврежденности монолитных идискретных материалов при проектировании дорожных конструкций

Новиков Артем Юрьевич, магистрант

Сибирская государственная автомобильно-дорожная академия

Выполнен обзор и анализ критериев прочности и условий пластичности монолитных и дискретных материалов, применяемых для устройства дорожных конструкций, и их методов расчета. Рассмотрены наиболее часто применяемые решения, в том числе полученные в последнее время. Определена область применения каждого метода расчета. Предложены способы расчета поврежденности в монолитном и дискретном материале через отношение модулей упругости и плотности поврежденных и неповрежденных тел.

Ключевые слова: дорожная конструкция, земляное полотно, основание, покрытие дорожная одежда.

Интенсивная автомобилизация РФ привела к тому, что автомобильные дороги стали подвергаться воздействию тяжелых, зачастую сверхнормативных, нагрузок с высокой интенсивностью движения. Это наносит значительный ущерб дорожной конструкции, включающей в себя дорожную одежду и земляное полотно. Появление на покрытиях дорожных одежд многочисленных повреждений повлекло взимание с большегрузных автомобилей платы за проезд по федеральным дорогам общего пользования.

Специалисты дорожной отрасли отреагировали модификацией существующих методов расчета дорожных одежд и разработкой принципиально новых способов проектирования дорожных конструкций. К числу таких методов отнесем:

 расчет дорожных конструкций по критериям ровности [1–3], включающий в себя расчет остаточных деформаций в грунтах земляного полотна [4–10] и конструктивных слоях дорожной одежды [11–16];

 расчет грунтов земляного полотна по сопротивлению сдвигу [17, 18], для которого совершенствуют условия пластичности [19–24], модели расчета главных и касательных напряжений [25–29];

 расчет грунтов земляного полотна по безопасным давлениям [30, 31];

 расчет монолитных слоев дорожной с учетом повреждений структуры материала [32, 33];

 разработку способов расчета шероховатости дорожных покрытий [34–36].

Кроме методов проектирования дорожных одежд интенсивно развивают технологические процессы, связанные с уплотнением грунтов и дискретных материалов. При этом пристальное внимание уделяют контролю степени уплотнения [37–39]. Для прогнозирования влияния коэффициента уплотнения грунта и дискретных материалов на их параметры прочности и деформируемости можно использовать математические модели, полученные в работах [34–36]. Общий вид таких зависимостей представлен автором в табл. 1.

Таблица 1

Математические модели для определения модуля упругости ипараметров прочности на сдвиг

Показатель прочности или деформируемости	Формула
Модуль упругости, МПА
Сцепление, МПа
Угол внутреннего трения, о

Примечание k_у — коэффициент уплотнения; W — (W=W_е/ W_т) относительная влажность; W_е — влажность грунта; W_т — влажность на границе текучести; a, b, c, d, f, g, h, k, l и m — параметры материала или грунта

Безусловно, что увеличение коэффициента уплотнения благоприятно влияет на показатели прочности и деформируемости грунтов и материалов с дискретной структурой. Однако, несмотря на такое положительное влияние состояние дорог РФ неудовлетворительное. Поэтому наиболее актуальной является разработка или совершенствование методов расчета дорожных одежд.

В этом аспекте наибольший интерес представляет совершенствование критериев прочности и условий пластичности монолитных и дискретных материалов, применяемых в дорожной конструкции. Для учета усталостных процессов, протекающих в этих материалах, применяют функциональные зависимости, описывающие уменьшение параметров прочности и деформируемости от числа приложенных расчетных нагрузок [4, 17, 24].

Вместе с тем возможен другой способ учета усталости материалов состоящий в том, что в критерии прочности и условия пластичности вводятся меры теории накапливания повреждений, которые называют сплошность Л. М. Качанова и поврежденность Ю. Н. Работнова [40]. Для ввода этих мер в критерий прочности или условие пластичности применяют принцип эквивалентности напряжений, состоящий в том, что напряжение в поврежденном теле находят по формуле:

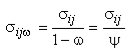(1)

где ij компоненты тензора напряжений сплошного тела;  — поврежденность Ю. Н. Работнова, — сплошность Л. М. Качанова.

Инварианты тензора напряжений, а так же напряжения на октаэдрических площадках и интенсивности Мизеса определяют по формулам механики сплошной среды, но с постановкой в них компонент тензора напряжений поврежденного тела. Поэтому инвариантные характеристики тензора напряжений поврежденного тела содержат либо сплошность, либо поврежденность. Формулы для их расчета приведены в таблице 2.

Таблица 2

Характеристики напряженного состояния поврежденного тела [17, 32, 33]

Наименование характеристики	Формула
Главные напряжения 1, 2, 3	; ;, где 1, 2 и 3 — главные напряжения в неповрежденном теле
Максимальные касательные напряжения max	;
Октаэдрическое нормальное напряжение окт и касательное окт напряжения	;
Интенсивность нормальных и и касательныхи напряжений	;.
Инварианты тензора напряжений (первый I1, второй I2 и третий I3)	; ; .
Второй инвариант девиатора напряжений	,
Третий инвариант девиатора напряжений	.

Подставляя зависимости таблицы 2 в критерии прочности и условия пластичности сплошных сред, получают их аналоги, но для поврежденных тел. Способ такой модификации показан в работах [17, 32, 33, 40]. Применяя критерий В. В. Чусова [40], полученный модификацией трехпараметрического условия пластичности Кулона-Мора [23, 24], запишем:

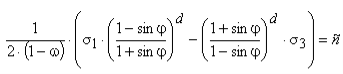(2)

где  — угол внутреннего трения; с — сцепление, МПа; d — параметр материала, зависящий от величины деформации, принимаемой за предельную при выполнении трехосных испытаний.

В критерии пластичности (2) основную задачу составляет расчет поврежденности. Одним из вариантов решения этой задачи является применения принципа эквивалентности деформаций [40, 41], из которого следует, что модули упругости поврежденного и неповрежденного тела связаны зависимостью:

(3)

Выразив из (3) поврежденность и подставив полученную формулу в критерий (2) получим:

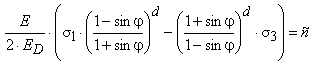(4)

Из анализа формулы (4) следует, что чем меньше модуль упругости поврежденного тела E_D, тем выше касательное напряжение определяемой левой частью уравнения (4).

Со временем появились новые данные о накапливании повреждений в материалах, работающих под нагрузкой и наряду с принципом эквивалентности деформаций возник другой постулат, известный как принцип энергетической эквивалентности [42]. Согласно этому принципу поврежденность так же определяется через отношение модулей упругости поврежденного тела и неповрежденной среды, но по иному выражению, которое имеет вид [42–4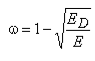5].

(5)

Подставив зависимость (5) в критерий 2, получим:

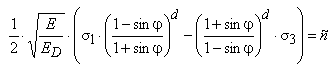(6)

Опираясь на данные работ [42–45] автор отметит, что критерий (6) более точен по сравнению со своим аналогом (4).

Оценивая область применения критерия (6) укажем, что он подходит для оценки начала пластичности в монолитных и дискретных материалах. Тем не менее, можно предложить несколько иной способ расчета поврежденности, используя соотношение плотностей поврежденного и сплошного тела. Дж. Леметр отметил, что в случае чистого пластичного повреждения, дефекты полости, которые могут быть приведены к сферической форме увеличиваются в диаметре [46]. Это означает, что объем среды увеличивается с повреждением, а плотность при той же массе уменьшается.

Так как плотность материала измерима, то к вычислению поврежденности можно применить принцип F. Moussy, рассмотревшего изменение относительной плотности при поврежденном и начальном состояниях, характеризуемых плотностями _D и  соответственно [47]. Для расчета плотности сплошного и поврежденного тела применены формулы работы [48]. После всех необходимых преобразований поврежденность определяется по формуле:

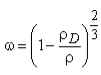(7)

Применяя зависимость (7) в условии пластичности (2), получим:

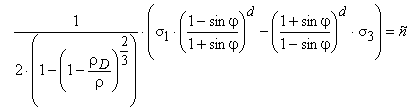(8)

Зависимость (8) удобна тем, что ее можно применить при оценке поврежденности дискретных и монолитных материалах, уложенных в конструктивные слои дорожной одежды и земляного полотна, непосредственно при эксплуатации дороги. Для этого достаточно определить плотность материала в конструктивном элементе, воспринимающем нагрузку, и так называемую, максимальную стандартную плотность, которую следует считать плотностью неповрежденного материала.

Применение этой зависимости позволяет корректировать расчет остаточного ресурса дорожной конструкции непосредственно в процессе эксплуатации автомобильной дороги.

Подводя итог, изложенным материалам автор отметит:

1. Предложенные в статье уравнения предельного состояния (4), (6) и (8) позволяют уточнить основные положения расчета дорожных конструкций, путем учета накапливания повреждений в монолитных и дискретных материалах.
2. Задачами дальнейших исследований автора являются экспериментальные работы, выполняемые в лаборатории, и натурные испытания дорожных конструкций для математического моделирования изменения модуля упругости и плотности материалов при воздействии многократных нагрузок.

Литература:

1. Александров А. С., Гордеева С. А., Шпилько Д. Н. О допускаемых и предельных значениях неровностей асфальтобетонных покрытий дорожных одежд жесткого типа // Автомобильная промышленность. — 2011. — № 2. — С. 31–35.

2. Герцог В. Н., Долгих Г. В., Кузин В. Н. Расчет дорожных одежд по критериям ровности. Часть 1. Обоснование норм ровности асфальтобетонных покрытий // Инженерно-строительный журнал. — 2015. — № 5(57) — С. 45–57.

3. Александров А. С. Критерии расчета дорожных конструкций по ровности, допускаемые и предельные неровности // Вестник гражданских инженеров. — 2008. — № 4. — С. 97–104.

4. Александров А. С. Применение теории наследственной ползучести к расчету деформаций при воздействии повторных нагрузок: монография. — Омск: СибАДИ, 2014. — 152 с.

5. Васильев А. П., Коганзон М. С., Яковлев Ю. М. Предложения по учету остаточных деформаций при расчете дорожных одежд нежесткого типа // Наука и техника в дорожной отрасли. — 1997. — № 1. — С. 5–6.

6. Александров А. С., Александрова Н. П., Кузин Н. В. методы теории наследственности в расчетах пластических деформаций материалов и грунтов при воздействии повторяющихся нагрузок // Транспортное строительство. — 2009. — № 2. — С. 25–28.

7. Александров А. С. Нелинейное пластическое деформирование материалов при воздействии повторных кратковременных нагрузок // известия высших учебных заведений. Строительство. — 2008. — № 10. — С. 74–84.

8. Каныгина С. Ю. Прогнозирование остаточных деформаций дорожных одежд нежесткого типа на земляном полотне из глинистых грунтов / С. Ю. Каныгина // Автореф. канд. техн. наук — М.: Изд-во МАДИ (ТУ), 1999. — 20 с.

9. Александров А. С. Моделирование деформационных процессов, протекающих в связных грунтах // Наука и техника в дорожной отрасли. — 2002. — № 4. — С. 16–19.

10. Александров А. С. Учет упруговязкопластических свойств связных грунтов при проектировании дорожных одежд // Автореферат канд. техн. наук — Омск: СибАДИ, 2001. — 24 с.

11. Семенова Т. В., Гордеева С. А., Герцог В. Н. Определение пластических деформаций материалов, используемых в дорожных конструкциях // Вестник Томского государственного архитектурно-строительного университета. — 2012. — № 4(37). — С. 247–254.

12. Александров А. С., Киселева Н. Ю. Пластическое деформирование гнейс- и диабаз материалов при воздействии повторяющихся нагрузок // Известия высших учебных заведений. Строительство. — 2012. — № 6. — С. 49–59.

13. Александров А. С. Пластическое деформирование гранодиоритового щебня и песчано-гравийной смеси при воздействии трехосной циклической нагрузки // Инженерно-строительный журнал. — 2013. — № 4(39) — С. 22–34.

14. Семенова Т. В., Герцог В. Н. Пластическое деформирование материалов с дискретной структурой в условиях трехосного сжатия при воздействии циклических нагрузок // Вестник Сибирской государственной автомобильно-дорожной академии. — 2013. — № 1(29). — С. 68–73.

15. Александров А. С. Расчет пластических деформаций материалов и грунтов дорожных конструкций при воздействии транспортной нагрузки // Строительная механика инженерных конструкций и сооружений. — 2009. — № 2. — С. 3–11.

16. Александров А. С., Долгих Г. В. Учет кратковременного и повторного характера приложения подвижной нагрузки в инженерных методах расчета остаточных деформаций грунтов и дискретных материалов дорожных конструкций // Вестник МАДИ. — 2011. № 4. — С. 81–87.

17. Александров А. С. Совершенствование расчета дорожных конструкций по сопротивлению сдвигу. Ч. 1. Состояние вопроса: монография. — Омск: СибАДИ, 2015. — 292 с.

18. Александров А. С., Долгих Г. В., Калинин А. Л. Один из путей совершенствования расчета дорожных одежд по условию сопротивления сдвигу в грунте земляного полотна // Модернизация и научные исследования в транспортном комплексе. — Пермь: Пермский национальный исследовательский политехнический университет, 2013. — С. 9–22.

19. Калинин А. Л. Применение модифицированных условий пластичности для расчета безопасных давлений на грунты земляного полотна. // Инженерно-строительный журнал — 2013. № 4(39). — С. 35–45.

20. Александров А. С., Долгих Г. В., Калинин А. Л. Применение критерия Друкера-Прагера для модификации условий пластичности // Наука и техника в дорожной отрасли. — 2013. № 2. — С. 26–29.

21. Александров А. С., Долгих Г. В. Калинин А. Л. Модификация критериев прочности сплошной среды для расчета грунтов земляного полотна по сопротивлению сдвигу // В сборнике: Архитектура. Строительство. Транспорт. Технологии. Инновации Материалы Международного конгресса ФГБОУ ВПО «СибАДИ». — Омск: СибАДИ, 2013. — С. 228–235.

22. Чусов В. В. Перспективы применения эмпирических условий пластичности грунтов и определение их параметров при трехосных испытаниях грунтов Вестник ВолГАСУ. — 2015. № 4(61). — С. 49–57.

23. Александров А. С., Калинин А. Л. Совершенствование расчета дорожных конструкций по сопротивлению сдвигу. Часть 1. Учет деформаций в условии пластичности Кулона-Мора // Инженерно-строительный журнал. — 2015. № 7(59). — С. 4–17.

24. Александров А. С. Совершенствование расчета дорожных конструкций по сопротивлению сдвигу. Ч. 2. Предложения: монография. — Омск: СибАДИ, 2015. — 262 с.

25. Александрова Н. П. Модифицированные модели для расчета главных напряжений в грунте земляного полотна // В сборнике: Архитектура. Строительство. Транспорт. Технологии. Инновации Материалы Международного конгресса ФГБОУ ВПО «СибАДИ». Омск, 2013. — С. 236–246.

26. Александров А. С. Один из путей расчета минимальных главных напряжений в грунтах земляного полотна / А. С. Александров // В сборнике: Архитектура. Строительство. Транспорт. Технологии. Инновации Материалы Международного конгресса ФГБОУ ВПО «СибАДИ». — Омск, СибАДИ, 2013. — С. 217–228.

27. Александров А. С., Долгих Г. В., Юрьев Д. В. Расчет главных напряжений в слоях дорожной одежды из дискретных материалов // Транспортное строительство. — 2011. — № 7. — С. 17–22.

28. Александрова Н. П., Семенова Т. В., Долгих Г. В. Совершенствование моделей расчета главных напряжений и девиатора в грунте земляного полотна // Вестник СИБАДИ. — 2014. — № 2(36). С. 49–54.

29. Александров А. С., Александрова Н. П., Долгих Г. В. Модифицированные модели для расчета главных напряжений в дорожных конструкциях из дискретных материалов // Строительные материалы. — 2012. — № 10. — С. 14–17.

30. Долгих Г. В. Расчет грунтов земляного полотна по критерию безопасных давлений // Вестник Сибирской государственной автомобильно-дорожной академии. — 2013. — № 6(34). — С. 43–49.

31. Александров А. С., Долгих Г. В., Калинин А. Л. О допускаемых давлениях на грунты земляного полотна и слои дорожной одежды // Наука и техника в дорожной отрасли. — 2012. № 2. — С. 10–13.

32. Александрова Н. П., Александров А. С., Чусов В. В. Модификация критериев прочности и условий пластичности при расчетах дорожных одежд // Вестник Сибирской государственной автомобильно-дорожной академии. — 2015. № 1(41). — С. 47–54.

33. Александрова Н. П., Александров А. С., Чусов В. В. Учет поврежденности структуры асфальтобетона в критериях прочности и условиях пластичности // В сборнике: Политранспортные системы материалы VIII Международной научно-технической конференции в рамках года науки Россия — ЕС. Новосибирск: СГУПС, 2015. — С. 219–225.

34. Семенова Т. В., Долгих Г. В., Полугородник Б. Н. Применение Калифорнийского числа несущей способности и динамического конусного пенетрометра для оценки качества уплотнения грунта // Вестник СибАДИ, 2014, № 1 — С. 59–66.

35. Александров А. С., Александрова Н. П., Семенова Т. В. О проектировании шероховатости дорожных покрытий и дождевой канализации по условиям безопасности движения // Автомобильная промышленность. — 2008. — № 8 — С. 36–38.

36. Александров А. С., Александрова Н. П., Семенова Т. В. Критерии проектирования шероховатых асфальтобетонных покрытий из условия обеспечения безопасности движения // Известия высших учебных заведений. Строительство. — 2009. — № 2. — С. 66–73.

37. Александров А. С., Семенова Т. В. Обеспечение сцепных качеств асфальтобетонных покрытий городских дорог и улиц при проектировании сети дождевой канализации // Вестник Московского государственного автомобильно-дорожного университета (МАДИ) — 2009. — № 2. — С. 29–32.

38. Александрова Н. П., Троценко Н. А. Применение измерителя жесткости грунта Geogauge для оценки качества уплотнения при операционном контроле // Вестник СибАДИ, 2014, № 3 — С. 40–47.

39. Александрова Н. П., Семенова Т. В., Стригун К. Ю. Совершенствование методов экспресс оценки качества уплотнения грунтов земляного полотна строительства автомобильных дорог // Вестник СибАДИ. — 2015. — № 4. — С. 46–57.

40. Чусов В. В. Применение теории накапливания повреждений в условиях пластичности асфальтобетона для расчета дорожных покрытий по сопротивлению сдвигу // Молодой ученый. — 2016. — № 6(110). — С. 221–227.

41. Lemaitre J. A course on damage mechanics. 2nd edn. — Springer: Berlin, Heidelberg, New York, 1996. P. 247.

42. Alves, M., Yu J., Jones, N. On the elastic modulus degradation in continuum damage mechanics. Computers and Structures 2000. Vol. 76. Pp. 703–712.

43. Cordebois J., Sidoro F. Damage induced elastic anisotropy. In: Boehler J, editor. Mechanical behaviour of anisotropic solids. London; Paris: Martinus Nijho Publishers; Editions du CNRS, 1979. Pp. 761–774.

44. Chow C. L., Lu T. L. On evolution laws of anisotropic damage. Engineering Fracture Mechanics. 1989. Vol. 34(3). Pp. 679–701.

45. Shen J. et al. Material damage evaluation with measured microdefects and multiresolution numerical analysis. International Journal of Damage Mechanics. 2014, Vol. 23(4) Pp. 537–566.

46. Lemaitre J., Dufailly J. Damage measurements. Engineering Fntcturr Mechanics 1987. Vol. 28. No. 516. — Pp. 643–661.

47. Moussy, F. Microstructure, endommagement et rupture ductile. Proc. d’ete franco — canadienne (1986).

48. Bompard D. P. Etfets endommageants de la porosite sur la propagation des fissures dans le Nickel fritte. These UTC (1986).
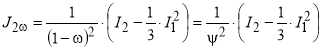