В статье приведён расчёт в котором была использована модель несжимаемая жидкость, которая предназначена для моделирования течения газа (жидкости) при больших числах Рейнольдса и при малых изменения плотности.
Ключевые слова: градирня, охлаждение воды, уравнений Навье-Стокса, численное моделирование.
Испарительное охлаждение воды используется в оборотных системах водоснабжения промышленных предприятий 1.
Компактные вентиляторные градирни наиболее эффективны с технической точки зрения, так как обеспечивают более глубокое и качественное охлаждение воды, выдерживая большие удельные тепловые нагрузки.
Процесс охлаждения происходит за счёт испарения части воды при стекании её тонкой плёнкой или каплями по специальному оросителю, вдоль которого в противоположном движению воды направлении подаётся поток воздуха. При испарении 1 % воды, температура оставшейся массы понижается на 5,48 °C 2.
Общее количество испаряющейся воды увеличивается с возрастанием поверхности контакта воды и воздуха, поэтому конструкции компактных вентиляторных градирен, в которых происходит испарительное охлаждение, предусматривают увеличение поверхности испарения путём создания большого зеркала жидкости, раздробления ее на струи и капли или образования тонких плёнок, стекающих по поверхности насадок. Возрастание интенсивности тепло- и массообмена при испарении достигается также повышением скорости газовой среды относительно поверхности жидкости. Однако увеличение этой скорости не должно приводить к чрезмерному уносу жидкости газовой средой и значительному повышению гидравлического сопротивления компактной вентиляторной градирни.
Часто наиболее надёжную информацию о физическом процессе можно получить путём непосредственных измерений. С помощью экспериментального исследования на полномасштабной установке можно определить поведение объекта в натурных условиях.
Численное решение задачи даёт подробную и полную информацию. С его помощью можно найти значения всех имеющихся переменных (таких, как скорость, давление, температура, концентрация, интенсивность турбулентности) во всей области решения. В отличие от эксперимента для расчёта доступна практически вся исследуемая область и отсутствуют возмущения процесса, вносимые датчиками при экспериментальном исследовании. Очевидно, что ни в одном экспериментальном исследовании невозможно измерить распределения всех переменных во всей исследуемой области. Поэтому, даже если проводится экспериментальное исследование, большое значение для дополнения экспериментальной информации имеют результаты численного решения.
Если с помощью численного решения изучаются закономерности физического процесса, а не сложные инженерные задачи, можно сконцентрировать внимание на нескольких существенных параметрах этого процесса и исключить все несущественные явления. При этом можно моделировать многие идеализированные условия, например, двухмерность, постоянство плотности, адиабатическую поверхность или бесконечно быструю реакцию. При экспериментальном исследовании даже с помощью довольно тщательного эксперимента не всегда можно достичь таких идеальных условий [3].
В настоящей работе представлены результаты расчётов трёхмерного турбулентного течения в полимерном оросителе компактных вентиляторных градирен. Численное моделирование выполнено для условий, принятых при проведении экспериментов.
С целью определения влияния размера и расположения оросителя на интенсивность теплообменных процессов в компактной вентиляторной градирне выполнен вычислительный эксперимент с использованием пакета FlowVision 4.
В качестве характерной области теплообмена рассматривался участок оросителя, расположенный в градирне. Форма данной области принята прямоугольной с вертикально направленной осью. Высота оросителя в градирне — 2 м, размер разреза — 0,5
0,75 м. На нижнем торце оросителя задана скорость восходящего воздушного потока, равная 1 м/с. Стенки градирни являются непроницаемыми.
Отметим, что, приведённые выше, параметры назначены в качестве граничных условий решения рассматриваемой задачи из условия максимального соответствия реальным процессам теплообмена в компактных вентиляторных градирнях.
Данные, полученные в результате численного моделирования по распределению в расчётной области скорости воздуха, приведены на рис. 1. Расчёты выполнены на основе модели совершенного газа. Принималось, что течение описывается системой стационарных трёхмерных уравнений Навье-Стокса и энергии, осреднённых по Рейнольдсу.
Сравнение результатов расчётов по программе FlowVision и экспериментальных данных свидетельствует о хорошем качественном и количественном предсказании поля скоростей и давление в оросителе градирни. С достаточной для практики точностью воспроизведена зона существенного повышения давления вблизи входа воздуха в ороситель и правильно предсказана форма распределения скоростей в канале и за выходом из оросителя. Картина распределения давления, полученного с использованием пакета FlowVision, качественно совпадает с данными эксперимента, однако в количественном выражении программа FlowVision даёт в среднем на 3 % заниженные по сравнению с экспериментом значения.
а)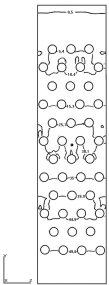
б)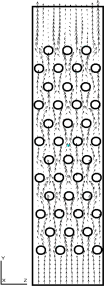 
Рис. 1. Распределение изолиний давления (а) и полей векторов скоростей (б) воздуха на поверхности оросителя в компактной вентиляторной градирне.
С использованием исследовательской программы FlowVision выполнены расчёты трёхмерного турбулентного течения в оросителе компактной вентиляторной градирни.
Сравнение с экспериментом показало, что при использовании модели турбулентности вычислительные системы позволяют хорошо предсказать структуру течения в канале оросителя, достаточно точно разрешая детали вторичных течений.
Литература:
- Пономаренко В. С., Арефьев Ю. И. Градирни промышленных и энергетических предприятий. — М.: Энергоатомиздат, 1998. — 376 с.
- Бэрджер Р. Влияние насадки градирен на экономические результаты их работы / Нефтегазовые технологии, 2000, № 6.
- S. Patankar «Numerical heat transfer and fluid flow». Hemisphere Publishing Corporation, New York, 1980.
- FlowVision. Система моделирования движения жидкости и газа. Версия 2.3.3. Руководство пользователя, 1999–2007.
