Известно, что поверхность цилиндра имеет систему прямых линий, параллельных оси цилиндра, а следовательно, и друг другу. Эти прямые называются образующими цилиндра.
Зададим на поверхности цилиндра две точки Аи В (рис.1-а). Будем искать среди кривых, расположенных на цилиндре и соединяющих точки Аи В, ту, которая обладает наименьшей длиной. Обозначим эту кратчайшую кривую, соединяющую точки Аи В, через АВ. Сначала рассмотрим случай, когда Аи В не лежат на одной образующей.
Разрежем боковую поверхность цилиндра по некоторой образующей РQ (не пересекающей АВ) и развернем ее на плоскость; получим некоторый прямоугольник (рис.1-б) (одна пара сторон прямоугольника, Р′Р″ и Q″Q″, получилась от развертывания окружностей, ограничивающих боковую поверхность цилиндра; друга пара P′Q′ и P″Q″, образовалась из двух краев разреза РQ). Образующие цилиндра перейдут в прямые, параллельные стороне Р′Q′ прямоугольника. Точки Аи В перейдут в точки А′и B′ лежащей внутри прямоугольника. Линии, соединяющие на цилиндре точки Аи В, перейдут в плоские линии, соединяющие точки А′ и B′ внутри прямоугольника. Дуга АВ — кратчайшая из линий на цилиндре, соединяющих точки Аи В — перейдет в кратчайшую из плоских линий, соединяющих точки А′ и B′ т. е. в прямолинейный отрезок А′ B′. Таким образом, после развертывания боковой поверхности цилиндра в плоский прямоугольник кратчайшая дуга АВ на поверхности цилиндра переходит в прямолинейный отрезок А′B′. Образующие цилиндра Р1Q1, Р2Q2 … переходит в прямые Р1′Q1′, Р2′Q2′ …, параллельные сторонам Р′Q′, Р″Q″ прямоугольника Р′Q′, Q″Р″. Углы, которые образует отрезок А′B′ с этими прямыми, равны как соответственные углы при параллельных линиях. Обозначим величину каждого из них через α.
Теперь свернем прямоугольник Р′Q′, Q″Р″ (склеив его противоположные стороны Р′Q′ и Р″ Q″) так, чтобы он вновь принял первоначальную форму цилиндра. Точки А′ и В′ перейдут вновь в точки А и В цилиндра, а прямолинейный отрезок А′В′, их соединяющий- в кратчайшую дугу АВ на поверхности цилиндра; углы отрезка А’В’ с прямыми Р1′Q1′, Р2′Q2′ перейдут в равные им углы между дугой АВ и образующими Р1′Q1′, Р2″ Q2″ …цилиндра. Так как прямая А’В’ пересекла все прямые, параллельные Р′Q′, под равными углами α, то кратчайшая дуга АВ в которую переходит А′В′, пересекает все образующие цилиндра под равными углами α (рис.1-а).
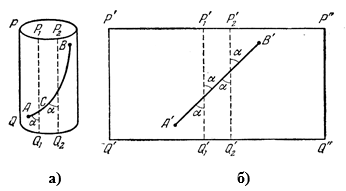
Рис. 1.
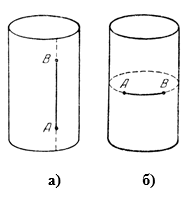
Рис. 2.
Рассмотрим особый случай, когда точки Аи В лежат на одной образующей (рис.2-а). В этом случае, очевидно, отрезок АВ образующей будет кратчайшим расстоянием между точками А и В на поверхности цилиндра.
Выделим еще случай, когда точки Аи В лежат на одном круговом сечении цилиндра (рис.2-б). Дуга АВ этого сечения перпендикулярна ко всем образующим. Она служим кратчайшей дугой, соединяющей точки А и В.
Если разрезать цилиндр по образующей, не пересекающей дуги АВ, и развернуть его в плоский прямоугольник, то в двух особо рассмотренных случаях кратчайшая дуга перейдет в отрезок, параллельный сторонам прямоугольника. Во всех остальных случаях кратчайшая линия пересекает образующие под углом, отличным от прямого (и не равным нулю).
Винтовой линией называется линия на поверхности цилиндра, которая пересекает все образующие цилиндра под равными углами, отличными от прямого.
Будем обозначать угол между винтовой линией и образующие через α. Линия, пересекающая образующие цилиндра под прямым углом, есть круговое сечение. Можно рассматривать круговое сечение как предельный случай винтовой линии, когда α обращается в прямой угол. Точно так же образующую цилиндра можно рассматривать как другой предельный случай, когда α обращается в нуль.
Рассмотрим два движения по поверхности цилиндра: движение параллельное оси (по образующей), и вращение вокруг оси (по круговому сечению) с постоянными скоростями.
Каждое из этих движений можно вести в двух противоположных направлениях. Будем считать на вертикальном цилиндре движение вверх положительным вращением вращение на вертикальном цилиндре справа налево (для того, кто стоит вдоль оси головой вверх), или против движения часовой стрелки. Будем считать отрицательным вращением вращение слева направо — движению часовой стрелки.
Движение по винтовой линии получается в результате складывания двух движений: движения, параллельного оси цилиндра, и вращения вокруг оси. Винтовая линия называется правой, если по ней движение вверх сочетается с положительным вращением — справа налево (рис. 3), левой, если по ней движение вверх сопровождается отрицательным вращением (слева направо).
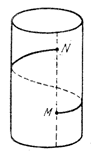
Рис. 3.
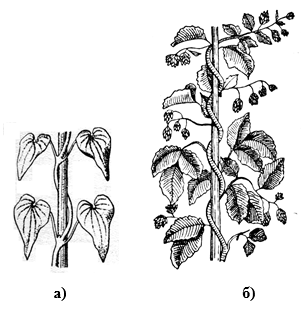
Рис.4
Большинство вьющихся растений (вьюнок, фасоль), завиваясь вокруг вертикальной опоры, принимает форму правых винтовых линий (рис.4-а). С другой стороны, хмель, например, принимает форму левой винтовой линии (рис.-4б).
Пусть, двигаясь по винтовой линии, точка пересечет некоторую образующую в точке М, а при продолжении движения по винтовой линии она вновь пересечет эту же образующую в точке N; когда точка прошла дугу MN винтовой линий, она совершила полный оборот вокруг оси цилиндра; в это же время она прошла вверх расстояние, равное длине отрезка MN (рис.3). Если скорость вращательного движения равно нулю, и точка перемещается только параллельно оси цилиндра по образующей, наступает первый предельный случай; другой предельный случай наступит, если скорость перемещения, параллельного оси цилиндра, равна нулю и точка только вращается вокруг оси по окружности.







