Краевые задачи для невырождающихся нагруженных уравнений смешанного типа второго и третьего порядка, когда нагруженная часть содержит след или производную от искомой функции изучены в работах А. М. Нахушева [1], Н. Н. Ланина [2], В. А. Елеева [3], Б.Исломова и Д. М. Курьязова [4, 5].
Несколько нам известно, краевые задачи типа задачи Трикоми и Геллерстедта для вырождающегося нагруженного уравнения смешанного типа второго порядка исследовались сравнительно мало. Отметим работы В. М. Казиева [6], Б.Исломова и Ф.Джураева [7]. Исходя из этого, настоящая работа посвящена постановке и исследованию краевой задачи типа задачи Геллерстедта, для нагруженного уравнения параболо-гиперболического типа в виде
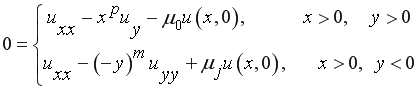
![]()
где ![]() - любые действительные числа, причем
- любые действительные числа, причем
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
. ![]()
Пусть ![]() — область, ограниченная отрезками
— область, ограниченная отрезками ![]() ,
, ![]() ,
, ![]() ,
, ![]() прямых
прямых ![]() ,
, ![]() ,
, ![]() ,
, ![]() соответственно, при
соответственно, при ![]() ;
; ![]() — характеристический треугольник, ограниченный отрезком
— характеристический треугольник, ограниченный отрезком ![]() оси
оси ![]() и двумя характеристиками
и двумя характеристиками
![]()
![]()
![]()
![]() уравнения
уравнения ![]() , выходящими из точки
, выходящими из точки ![]() ,
, ![]() и пересекающимися в точке
и пересекающимися в точке 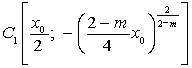 ;
; ![]() — характеристический треугольник, ограниченный отрезком
— характеристический треугольник, ограниченный отрезком ![]() оси
оси ![]() и двумя характеристиками
и двумя характеристиками ![]()
![]()
![]()
![]() уравнения
уравнения ![]() , выходящими из точек
, выходящими из точек ![]() ,
, ![]() и пересекающимися в точке
и пересекающимися в точке 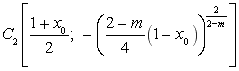 ;
; ![]() — характеристический четырёхугольник, ограниченный характеристиками
— характеристический четырёхугольник, ограниченный характеристиками ![]() ,
, ![]() и
и ![]()
![]() ,
, ![]()
![]() уравнения
уравнения ![]() , пересекающимися в точках
, пересекающимися в точках ![]() ,
, ![]() ,
, ![]() и
и 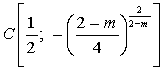 при
при ![]() , причем
, причем ![]() .
.
Введем следующие обозначения:
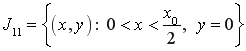 ,
, 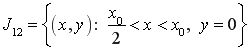 ,
,
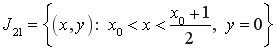 ,
, 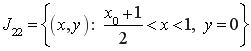 ,
,
![]() ,
, ![]() ,
,
![]() , причем
, причем ![]()
![]()
В области ![]() для уравнения
для уравнения ![]() исследуются аналоги задачи Геллерстедта.
исследуются аналоги задачи Геллерстедта.
Задачи. Найти функцию ![]() , обладающую следующими свойствами:
, обладающую следующими свойствами:
1) ![]() ;
;
2) ![]() является регулярным решением уравнения
является регулярным решением уравнения ![]() в областях
в областях
![]()
![]() ;
;
3) ![]() удовлетворяет краевым условиям
удовлетворяет краевым условиям
![]() ,
, ![]() ,
, ![]() ,
, ![]()
![]() ,
, ![]() ,
, ![]()
4) на линии вырождения ![]() выполняется условия склеивания
выполняется условия склеивания
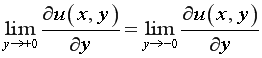 ,
, ![]()
равномерно при ![]()
![]() ,
,
где ![]() ,
, ![]() ,
, ![]() ,
, ![]() — заданные функции, причем
— заданные функции, причем ![]() ,
,
![]() ,
, ![]()
![]() ,
, ![]()
![]()
Теорема. Если выполнены условия ![]() ,
, ![]() ,
, ![]() и
и ![]() то в области
то в области ![]() существует единственное решение задачи.
существует единственное решение задачи.
Литература:
- Нахушев А. М. Нагруженные уравнения и их приложения. //«Дифференциальные уравнения». 1983. Т.19. № 1. С. 86–94.
- Ланина И. Н. Краевая задача для одного нагруженного гиперболо-параболического уравнения третьего порядка. //«Дифференциальные уравнения». 1981. Т. 17. № 1. С. 97–106.
- Елеев В. А. О некоторых краевых задачах для смешенных нагруженных уравнений второго и третьего порядка. //«Дифференциальные уравнения». 1994. Т. 30. № 2. С. 230–237.
- Исломов Б., Курьязов Д. М. Об одной краевой задаче для нагруженного уравнения второго порядка // «Доклады АН РУз». 1996. № 1–2. С.3–6.
- Исломов Б., Курьязов Д. М. Краевые задачи для смешанного нагруженного уравнения третьего порядка параболо-гиперболического типа. // «Узбекский математический журнал». 2000. № 2. С. 29–35.
- Казиев В. М. О задаче Дарбу для одного вырождающегося нагруженного интегро-дифференциального уравнения второго порядка. //«Дифференциальные уравнения». 1978. Т.14. № 1. С.181–184.
- Исломов Б., Джураев Ф. Аналог задачи Трикоми для вырождающегося нагруженного уравнения параболо-гиперболического типа. // «Узбекский математический журнал». 2011. № 2. С. 75–85.







