Роль больших простых чисел в современной криптографии
Норматов Шербек Бахтиёрович, старший преподаватель
Каршинский филиал Ташкентского университета информационных технологий (Узбекистан)
В этой статье проанализирована роль больших простых чисел в современной криптографии, вычисление количества простых чисел в заданном диапазоне, методы проверки числа на простоту и принцип использования таблиц простых чисел.
Ключевые слова: информационная безопасность, криптография, простые числи, алгоритмы шифрование, проверка числа на простоту.
Бурное развитие информационных и коммуникационных технологий повышает актуальность проблемы информационной безопасности. В связи с этим требуется разработать ряд новых методов и средств, направленных на обеспечение информационной безопасности. Следовательно, требуется комплексный подход для надежного обеспечения информационной безопасности. Другими словами, возникает необходимость эффективного использования правовых, организационных и инженерно-технических обеспечений защиты информации.
В частности, криптографические методы играют важную роль в защите информации. Сегодня широко используется криптографические системы защиты информации. Все эти криптографические системы работают на основе криптографического алгоритма. В настоящее время в качестве основы для многих криптографических стандартов берутся алгоритмы RSA и Эль-Гамаль. Эти алгоритмы основаны на задаче факторизации и дискретном логарифмировании в конечном поле.
Для шифрования данных и создания электронной цифровой подписи в обоих алгоритмах используются 1024-битные и большие простые чисел. Таким образом, генерирование и работа с большими простыми числами стали одним из главных вопросов в криптографии. В общем, причиной широкого использования простых чисел в криптографии является трудность обнаружения этих чисел.
Простые числа — это целые натуральные числа больше единицы, которые имеют ровно 2 натуральных делителя (только 1 и самого себя), т. е. не делятся ни на одно другое число, кроме самого себя и единицы [2]. Давно уже проводятся исследования, посвященные генерации простых чисел. Однако до сих пор не было найдены только генерирующие функции числа [1]. Причиной этого можно назвать отсутствие возможности описания простых чисел с помощью тех или иных натуральных чисел. Кроме того, простые числа неравномерно расположены в среде натуральных чисел. Имеется неограниченное количество простых чисел. То есть, ими можно пользоваться сколько угодно. Но они мало встречаются среди натуральных чисел.
Определяем общее количество всех 32-битных натуральных чисел и 32-битных простых чисел.
Самое большое 32-битное число
![]()
Теперь вычислим количество всех простых чисел в данном интервале. Можно определить количество простых чисел, разряд не выше чем ![]() , следующим образом по формуле Лежандра:
, следующим образом по формуле Лежандра:
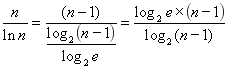
Количество, не превышающее 32 уровни простых чисел, можно вычислить следующим образом:
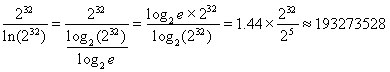 (Здесь,
(Здесь,![]() ).
).
Количество, не превышающее 31 уровня простых чисел, можно вычислить следующим образом:
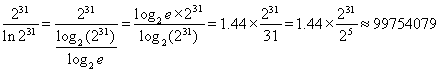
Таким образом, количество 32-битных простых чисел равно ![]() Значит, можно сделать вывод о том, что существует единое простое число в каждой 30 чисел в этом интервале.
Значит, можно сделать вывод о том, что существует единое простое число в каждой 30 чисел в этом интервале.
Мы можем отобразить 32-битное число по следующему выражению:
|
1 |
1 |
![]()
![]()
![]()
Для того что бы использовать 32-разрядное число, последний разряд должен быть равен единице. Первый разряд равен единице, что означает, число является нечетным. Все простые числа являются нечетными, так что придётся игнорировать все четные числа.
В алгоритме генерирования простых чисел в данном интервале предусматриваются следующие две задачи:
а) выбор числа в данном интервале;
б) проверка чисел на простоту.
Если выбранное число из данного интервала является простым, то оно добавляется в таблицу простых чисел. В противном случае придётся выбрать другое число и проверить его на простоту (1-схема).
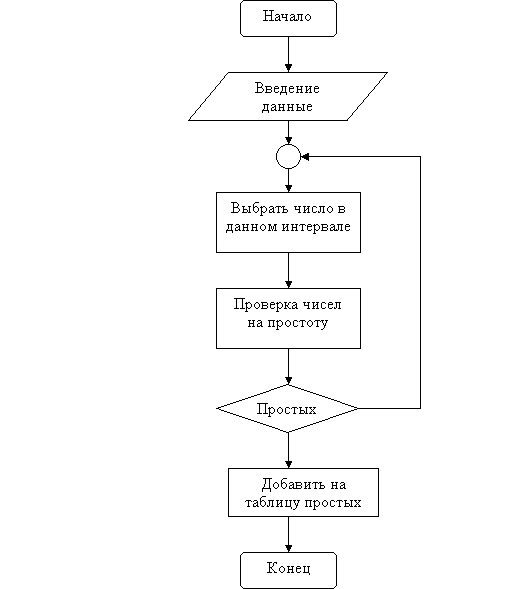
Рис. 1. Алгоритм генерация простых чисел.
Последовательный выбор чисел требует больше времени, также использование ряда выбранных простых чисел снижает криптостойкость алгоритмов шифрования. Поэтому, чтобы достичь требуемой эффективности, надо выбрать число случайным образом. Для случайного выбора числа в заданном интервале, используются специальные стандартные функции случайных величин. Эта функция существует во многих языках программирования.
Следующей задачей является проверка выбранного числа на простоту. Существуют некоторые вероятностные тесты на простоту. Одним из них является тест Рабина-Миллера, который основан на идею малой теоремы Ферма.
Малая теорема Ферма утверждает, что если ![]() простое число, то выполняется условие: при всех
простое число, то выполняется условие: при всех ![]() имеет место сравнение
имеет место сравнение ![]() Если для некоторого
Если для некоторого ![]() имеет место соотношение
имеет место соотношение ![]() , то говорят, что число
, то говорят, что число ![]() является простыми по основанию
является простыми по основанию ![]() [4].
[4].
Сначала обозначаем
Любое двоичное число может быть обозначено как: ![]()
![]() Если вынести за скобки
Если вынести за скобки ![]() , получим следующее выражение:
, получим следующее выражение: ![]() здесь
здесь ![]()
![]() и
и ![]() , иначе число считается четным. Если
, иначе число считается четным. Если ![]() и вынести за скобки
и вынести за скобки ![]() то
то ![]() Где
Где ![]()
![]()
Если ![]() выражение устраивает, тогда число считается нечетным. Если
выражение устраивает, тогда число считается нечетным. Если ![]() то вынести за скобки
то вынести за скобки ![]() получиться
получиться ![]() Где
Где ![]()
![]()
а) если ![]() , то
, то ![]() и
и ![]() является простыми числами с вероятностями.
является простыми числами с вероятностями.
б) если ![]() не устраивает, тогда проверяется
не устраивает, тогда проверяется ![]() .
.
Если ![]() , то
, то ![]() и
и ![]() является простыми числами с вероятностями. Если отношение
является простыми числами с вероятностями. Если отношение![]() не устраивает, тогда проверяется
не устраивает, тогда проверяется ![]() .
.
Точно также проверяется степень до ![]() раза. Если во всех случаях
раза. Если во всех случаях ![]() отношения
отношения ![]() не устраивает, тогда
не устраивает, тогда ![]() не является простыми.
не является простыми.
Если во всех ![]() случаях
случаях ![]() уточняется,
уточняется, ![]() является простыми с
является простыми с ![]() вероятностями [3].
вероятностями [3].
Необходимо учитывать следующие вопросы генерации больших простых чисел:
а) выбора числа случайном образом в данном интервале;
б) распределения найденных простых чисел в таблице простых чисел;
в) при необходимости из таблицы простых чисел выбрать последовательным или случайным образом.
Литература:
- Алгебра теория чисел. II часть. Р. Н. Назаров, Б. Т. Тошпулатов, А. Д. Дусимбетов. “Тошкент” 1995.
- Нильс Фергюсон, Брюс Шнайер. Практическая криптография. Москва. Санкт-Петербург. Киев. 2005. 421 стр.
- http://www.sans.org/reading-room/whitepapers/vpns/prime-numbers-public-key-cryptography-969
- http://home.sandiego.edu/~dhoffoss/teaching/cryptography/10-Rabin-Miller.pdf







