Одной из целей реализации федеральных государственных образовательных стандартов (ФГОС) второго поколения является формирование у учащихся целостных знаний об окружающем мире. В рамках урочной деятельности это достигается через установление связей между содержанием различных учебных предметов. Интеграция в этом направлении способствует достижению учащимися метапредметных и личностных образовательных результатов, повышает уровень усвоения предметных знаний. Но организация такой деятельности на уроках осложняется строго ограниченным временем учебного занятия, насыщенностью предметного материала. Поэтому целесообразно организовать работу, направленную на познание школьниками окружающего мира и связей между учебными предметами, во внеурочной деятельности на школьном уровне.
В качестве интегрирующей основы занятий может выступать процесс погружения в эпоху появления различных математических игр и головоломок. Такой выбор обусловлен следующим:
- Первые математические игры появились более 5000 лет назад. Изучение учащимися истории появления и развития игр у различных народов позволяет организовать ненавязчивое знакомство детей с достижениями науки и культуры различных этапов развития человечества.
- Погружение учащихся в атмосферу коллективной игры способствует решению проблемы ограниченности общения, недостатка коммуникативных навыков современных школьников.
- Математические игры являются средством развития мышления учащихся, способствуют повышению познавательного интереса.
Одной из форм реализации курса внеурочной деятельности, в основу которого положены математические игры и головоломки может быть математический клуб.
В соответствии с образовательными результатами, выделенными в ФГОС второго поколения, нами были разработаны требования к содержанию занятий математического клуба:
1) С целью достижения метапредметных образовательных результатов необходимо осуществлять интеграцию содержания различных учебных предметов.
2) Усвоение научных знаний, как правило, опирается на логику, а восприятие произведений искусства в основном основывается на эмоциональной сфере. Но, в целом, восприятие человеком культурных объектов строится на единстве логического и эмоционального. Поэтому материал для занятий должен быть подобран таким образом, чтобы развивать у учащихся логическое и эмоциональное восприятие любых ценностей материальной и духовной жизни в их единстве и многообразии [1]. Это будет способствовать формированию целостного мировоззрения учащихся, достижению ими личностных образовательных результатов.
С учетом этих требований нами были выделены этапы подготовки и проведения занятий математического клуба. Рассмотрим эти этапы на примере древней китайской игры Гомоку и погружения в эпоху Древнего Китая.
- Нулевой этап.На данном этапе учитель осуществляет:
а) выбор игры, определяет страну происхождения игры, выбор эпохи погружения;
б) поиск путей интеграции предметных знаний ребенка с искусством, бытом, нравственными аспектами и историческими событиями выбранной эпохи.
Установить связь между содержанием различных учебных предметов и окружающим ребенка миром можно с помощью метапредметных заданий.
В работе математического клуба используются метапредметные задания трех типов: состоящие из двух блоков; на установления соответствия, связи; на идентификацию [2]. Рассмотрим примеры заданий каждого типа.
- Структура задания состоит из двух блоков: интегрирующего — научно-популярного, популярного, научно-иллюстративного, художественно-иллюстративного текста; конкретизирующего — состоящего из вопросов.
Приведем пример задания, состоящего из двух блоков:
В окрестностях южнокитайского города Гуйлинь есть поразительно красивая пещера. Согласно легенде, свое название пещера получила от тростника, который прорастал неподалеку и издавна использовался для изготовления флейт. Пещера разделена на части, такие как «павильоны», «дворцовые палаты», «сады» и «парки». Пещера была образована порядка двухсот миллионов лет назад и, возможно, никогда не была бы обнаружена людьми, если бы не природные катаклизмы. Ее протяженность составляет около 1 ли, а в глубину она уходит на ![]() от максимальной глубины глубочайшего озера планеты. Первые упоминания о посещении данной пещеры были зафиксированы во времена правления династии Танг.
от максимальной глубины глубочайшего озера планеты. Первые упоминания о посещении данной пещеры были зафиксированы во времена правления династии Танг.
а)Как называется пещера?
б)Сколько лет назад были зафиксированы первые упоминания о пещере?
в)Какова протяженность пещеры в метрах?
г)Подберите изобразительно-выразительные средства (эпитеты, сравнения), помогающие охарактеризовать пещеру
д)Найдите глубину пещеры.
е)Благодаря чему была обнаружена эта пещера?
ж)Придумайте 2–3 объяснения происхождения названия Тростниковой пещеры, которые будут отличаться от древней легенды.
з)Какова роль пещер в жизни человека?
При выполнении таких заданий от учащихся требуется умение устанавливать связь между содержанием различных учебных предметов, применять полученные на уроках знания к объекту культуры, в данном случае к пещере «Тростниковая флейта». Такая деятельность направлена на достижение метапредметных результатов. Это соответствует первому выделенному нами требованию к содержанию занятий математического клуба.
Второе требование реализуется при ответе учащихся на вопросы к тексту, которые подобраны так, чтобы при восприятии учащимися пещеры «Тростниковая флейта» поддерживалась связь эмоционального и логического.
Рассмотрим пример задания на установление соответствия, связи:
В древнекитайской астрономии было известно только 5 планет, не считая планету Земля.
а)Посмотрите на фотографию (рис. 1). Как вы думаете, какие планеты были известны в Древнем Китае. Почему?
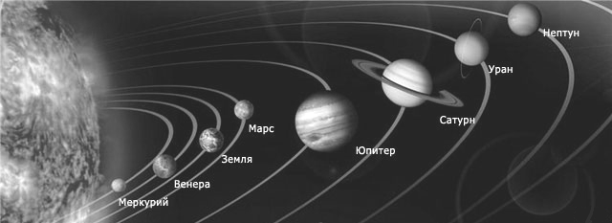
Рис. 1. Строение солнечной системы
б) Какая связь между фотографией и предложением: Морозным Вечером Залез на Мачту Юнга Стремясь Увидеть Незнакомый Порт?
Задания рассмотренного типа способствуют формированию таких познавательных УУД как установление причинно-следственных связей. Использование в заданиях рисунков, которые помогают учащимся ответить на вопросы задания, способствует формированию знаково-символических УУД.
- Рассмотрим пример задания на идентификацию.
Попробуйте угадать, что зашифровано на каждой карточке. Что объединяет все карточки?

Рис. 2. Карточки к заданию на идентификацию
Этот тип заданий способствует формированию познавательных УУД, в частности, умение работать с информацией, выдвигать гипотезы.
- Подготовительный этап.
Учителя разных предметов и учащиеся готовятся к собранию клуба заранее — создают элементы национальных костюмов, украшают кабинет в соответствии с тематикой, знакомятся с национальной кухней, изготавливают поля и фишки для игры, готовят «карточки» с интересными фактами, инсценируют притчу, легенду или басню. Уже в процессе подготовки дети применяют знания из различных учебных предметов — истории, географии, литературы, технологии и др.
- Основной этап.
Связь заданий, разработанных на нулевом этапе с планетами Солнечной системы, не случайна. По одной из версий появление игры Гомоку связано с развитием древнекитайской астрономии, а именно — открытием пяти планет, использованием доски и пяти камней для моделирования астрономических явлений.
Первая часть занятия математического клуба посвящена знакомству детей с этой версией через решение метапредметных заданий, в процессе выполнения которых учащиеся узнают о быте, достижениях науки и культуры Древнего Китая. Во второй части занятия участники математического клуба знакомятся с правилами игры Гомоку, играют в нее в парах сменного состава.
- Рефлексия.
На этом этапе осуществляется рефлексия настроения, эмоционального состояния, деятельности и содержания занятия.
Проведение занятий математического клуба в соответствии с описанными выше этапами будет обеспечивать целостность образовательного процесса, интеграцию содержания различных учебных предметов, и направлено на реализацию требований ФГОС ОО второго поколения.
Литература:
- Ариарский М. А.. Обогащение культурно-образовательной среды как средство повышения эффективности формирования личности // Сборник научных статей Исаакиевского собора «Кафедра XIV». — СПб.: ООО «Р-КОПИ», 2014. — С. 24–46.
- Подходова Н. С., Аранова С. В.. Межпредметные задания. Матричный классификатор межпредметных заданий. // Вестник САФУ. — 2012. — № 6. — С. 143–153.







