В статье исследуется проблема формирования позитивной мотивации у студентов посредством математического моделирования процесса принятия решений в профессионально ориентированных учебных задачах.
Ключевые слова:мотивация,профессионально ориентированные задачи, анализ проблемной ситуации, математическая модель задачи.
Успешность современного образовательного процесса в вузе определяется множеством факторов, важнейшим из которых является внутреннее желание, заинтересованность студентов в обучении. Как показывают исследования [1], фактор мотивации важен для успешной учебы сильнее, чем фактор интеллекта. Мотивационным потенциалом обладают, прежде всего, эмоции. Одной из приоритетных эмоций в обучении является интерес, который состоит в желании внести ясность в характеристику ситуации и проявляется в ощущении любопытства или желании исследовать незнакомые объекты [1].
Таким образом, преподаватель современного вуза сталкивается с проблемой формирования у студентов позитивной мотивации, что в свою очередь требует структурирования, психологически грамотного и методически оправданного преобразования научного знания и профессионально–ориентированного материала в учебный материал [2].
Так, целью изучения математических дисциплин программ бакалавриата направлений психолого-педагогического профиля является формирование у студентов базовых знаний основных разделов математики как средства исследования, моделирования и прогнозирования процессов и явлений профессиональной деятельности.
Достижение названной цели предполагает формирование соответствующих компетенций, компоненты которых включают:
− умение использовать математические модели явлений и процессов в профессиональной деятельности; обосновывать выбор теоретико-методологических основ исследования явлений и процессов в профессиональной сфере в контексте различных моделей научных картин мира;
− владение математическими методами в психолого-педагогических исследованиях.
Для анализа, прогнозирования и выбора оптимального решения в области психолого-педагогических исследований необходимым инструментом являются математические модели, которые достаточно хорошо могут описывать психолого-педагогические процессы и явления с использованием математического аппарата: функций, уравнений, неравенств, их систем [3].
Рассмотрим конкретные проблемные ситуации в области психолого-педагогических исследований и построим для них математические модели, по которым сможем найти решение проблемы. При этом будем использовать следующую схему моделирования проблемной ситуации:
- логический анализ проблемной ситуации (анализ проблемной ситуации предполагает выделение информационных данных и определение условий проблемной ситуации; установление связей между информационными данными и формулирование прикладной задачи);
- формулировка прикладной задачи;
- построение математической модели задачи (перевод условия прикладной задачи на математический язык);
- решение проблемы как математической задачи, расчеты по модели и их оценка;
- интерпретация (перевод математического решения обратно на язык, на котором была сформулирована исходная проблема), формулировка решения [4].
Проблемная ситуация № 1:
В результате проведенного тестирования по определению типа личности были выявлены следующие факты:
- если Аношин экстраверт, то и Ветров экстраверт;
- если Аношин не является экстравертом, то либо Ветров является экстравертом, либо Смирнов, причем не оба одновременно;
- если Ветров не является экстравертом, то Аношин экстраверт, а Смирнов — нет.
Необходимо выяснить, кто согласно указанным утверждениям является экстравертом.
Анализ проблемной ситуации:
Посмотрим на эту задачу с точки зрения двузначной алгебры логики. Мы имеем три составных истинных высказывания. Каждое из них состоит из простых высказываний, которые соединены логическими связками. Каждое простое высказывание это высказывание о том, является ли та или иная личность (Аношин, Ветров, Смирнов) экстравертом или не является. Для удобства можно ввести обозначения для простых высказываний: А — «Аношин — экстраверт», В — «Ветров — экстраверт», С — «Смирнов — экстраверт».
Сформулируем прикладную задачу:
Определить истинность простых высказываний А, В, С, пользуясь законами двузначной алгебры логики.
Построим математическую модель задачи:
Используя введенные обозначения для простых высказываний можно при помощи алгебры логики формализовать составные высказывания 1, 2, 3 следующим образом:
-
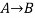 ;
;
-
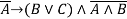 ;
;
-
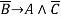 ;
;
Таким образом, получаем систему уравнений от трех переменных над двузначной алгеброй логики:
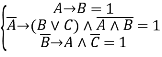
Решение проблемы как математической задачи:
Известно, что импликация ![]() может быть истинна в трех случаях (в зависимости от истинности высказываний
может быть истинна в трех случаях (в зависимости от истинности высказываний ![]() ). Рассмотрим по отдельности эти случаи:
). Рассмотрим по отдельности эти случаи:
-
Если
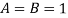 , то
, то
![]()
В этом случае получаем два решения ![]() .
.
-
Если
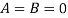 , то
, то
![]()
В этом случае получаем противоречие (последнее выражение противоречит алгебре логики).
-
Если
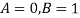 , то
, то
![]()
В этом случае получаем два решения ![]() .
.
Таким образом, получаем 4 набора решений: ![]() .
.
Интерпретация и формулировка решения:
Если внимательно посмотреть на полученные наборы решений, то можно заметить, что Ветров однозначно является экстравертом (во всех наборах ![]() ). Про остальных же ничего конкретного сказать нельзя, то есть они могут быть, так и не быть экстравертами.
). Про остальных же ничего конкретного сказать нельзя, то есть они могут быть, так и не быть экстравертами.
Проблемная ситуация № 2:
Проведена диагностика по трем тестам на определение степени самостоятельности, потребности в достижении и волевой саморегуляции. Затем произвели три выборки. Первая выборка человек получили по первому, второму, третьему тестам соответственно баллы 1, 4, 9. Вторая выборка человек получили по первому, второму, третьему баллы 1, 2, 3, соответственно. Третья выборка человек получили по первому, второму, третьему баллы 1,1,1 соответственно. При этом подсчитали, что все три выборки человек по первому тесту получили общий балл равный 2, по второму — 4, по третьему — 8. Требуется проверить правильность подсчетов итогов тестирования.
Анализ проблемной ситуации:
Оформим условие задачи в виде таблицы 1.
Таблица 1
Условие учебной задачи
|
|
Первый тест |
Второй тест |
Третий тест |
|
Первая выборка |
1 |
4 |
9 |
|
Вторая выборка |
1 |
2 |
3 |
|
Третья выборка |
1 |
1 |
1 |
|
Общий балл |
2 |
4 |
8 |
Предположим, что расчеты верные, тогда можно построить некоторую систему линейных уравнения (это можно сделать в силу «линейности» условий задачи), в которой сделаем неизвестными величинами количество человек в первой выборке, количество человек во второй выборке, количество человек в третьей выборке. Если решением системы будут не положительные числа, то, очевидно, в подсчете итогов тестирования есть ошибка, иначе, ничего сказать нельзя и нужно использовать другие методы.
Прикладная задача:
Определить знаки решений системы линейных уравнений, построенной по таблице 1, относительно количества человек в первой выборке, во второй выборке, в третьей выборке
Математическая модель задачи:
Пусть  .
.
Пользуясь данными таблицы 1 можно получить следующее матричное уравнение
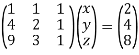 .
.
Решение проблемы как математической задачи:
Решим систему методом Крамера
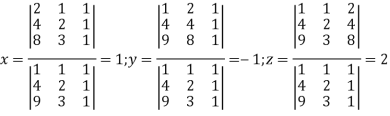 .
.
Получили, что ![]() .
.
Интерпретация и формулировка решения:
Таким образом, в подсчете итогов тестирования есть ошибка.
Приведенные решения учебных задач по предложенной схеме их моделирования — это один из возможных примеров использования профессионально ориентированных упражнений в образовательном процессе как приема управления эмоциями студентов в целях формирования у них позитивной направленности на обучение.
Литература:
- Долженко Р. А. Управление эмоциями студентов как основа формирования позитивной мотивации к обучению // Вестник Томского государственного университета. Экономика. 2011. № 1(13). С. 127–131.
- Атрощенко С. А., Нестерова Л. Ю. Активизация познавательной деятельности студентов посредством интерактивного обучения // Международный научно-исследовательский журнал. 2014. № 7–2(26). С. 49–51.
- Атрощенко С. А. Формирование у учащихся базовых математических моделей задач эффективного управления // Международный научно-исследовательский журнал — Research Journal of International Studies. 2013. № 7–4(14). С. 55–56.
- Атрощенко С. А., Феклистов С. В. Использование математических моделей в решении профессионально ориентированных задач // Электронный научно-практический журнал Культура и образование. 2015. № 3(19). С. 9.







