В механизме иглы движения точки ![]() игловодителя, будем рассматривать в неподвижной системе отсчета
игловодителя, будем рассматривать в неподвижной системе отсчета ![]() . Определяем ускорения точки
. Определяем ускорения точки ![]() игловодителя в крайних ее положениях
игловодителя в крайних ее положениях ![]() , предположим, что частота вращения кривошипа
, предположим, что частота вращения кривошипа ![]() . Тогда мы получим зависимость между скоростями
. Тогда мы получим зависимость между скоростями ![]() :
:
![]()
где: Ob — отрезок, отсекаемый на прямой OY1 , являющийся продолжением оси симметрии шатуна (рис.1).
Ускорение точки B определяем по выражениям:
![]()
![]()
![]()
тогда ![]() будет равен:
будет равен: 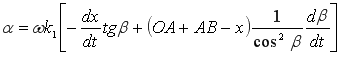 (1.1)
(1.1)
где: k1 — масштабный коэффициент для y=Ob, из формулы 1.1 видно, что
![]()
![]()
![]()
Поэтому для правого крайнего положения точки В имеем:
где: ![]() = r / l — коэффициент, определяющий равномерности хода игловодителя. Аналогично, для левого крайнего положения точки В имеем:
= r / l — коэффициент, определяющий равномерности хода игловодителя. Аналогично, для левого крайнего положения точки В имеем:
![]()
![]()
В соответствии с этим, по формуле (1.1) найдем ускорения точки В игловодителя в правом и левом крайних положениях: ![]()
Как известно, график функции в зависимости от пути игловодителя имеет вид: ![]()
где: S = k1x, — можно с достаточной точностью принять за параболу, которая проходит через точки ![]() и
и ![]() , а касательные к параболе в этих точках пересекаются в точке
, а касательные к параболе в этих точках пересекаются в точке ![]() , где:
, где: ![]() представляет абсциссу точки пересечения прямой d1e1с осью направляющей (рис. 2).
представляет абсциссу точки пересечения прямой d1e1с осью направляющей (рис. 2).
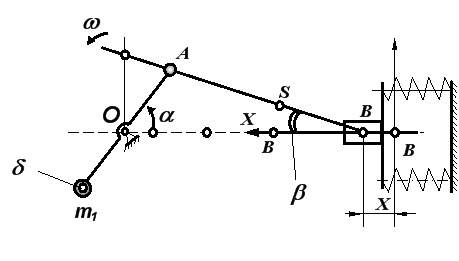
Рис. 1. Схема механизма иглы с упругой связью
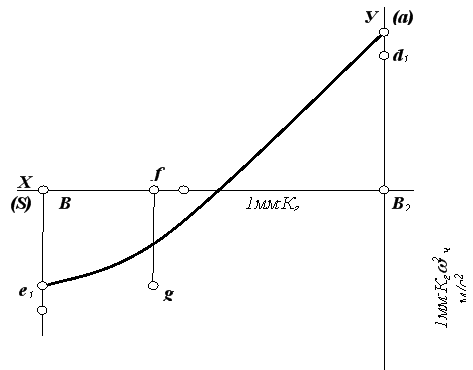
Рис. 2. График измения зависимоcти перемещения иглы от ускорения
Центр масс подвижных звеньев механизма определим вектором: ![]()
где:
![]() (1.2)
(1.2)
Тогда получим следующее равенство: ![]() представляющее условие уравновешенности вращающихся масс, к которым относятся масса т1кривошипа (рис. 2) и часть массы т2шатуна, приведенная статически к точке А кривошипа и равная
представляющее условие уравновешенности вращающихся масс, к которым относятся масса т1кривошипа (рис. 2) и часть массы т2шатуна, приведенная статически к точке А кривошипа и равная ![]() Таким образом, для реализации условия (1.2), кривошипу необходимо придать такую форму, чтобы его дисбаланс относительно оси вращения был:
Таким образом, для реализации условия (1.2), кривошипу необходимо придать такую форму, чтобы его дисбаланс относительно оси вращения был:
![]()
Если последнее условие выполняется, то центр масс подвижных звеньев механизма будет двигаться вдоль оси направляющей с ускорением ![]() . Поэтому по оси направляющей будет действовать неуравновешенная сила
. Поэтому по оси направляющей будет действовать неуравновешенная сила ![]() (1.3)
(1.3)
где: ![]() представляет поступательно движущуюся массу, состоящую из массы т3 игловодителя и шатунной массы:
представляет поступательно движущуюся массу, состоящую из массы т3 игловодителя и шатунной массы: ![]()
Снижение динамической нагрузки в кинематических парах от действия силы ![]() (S), будет вызывать динамические нагрузки, которые могут создавать не только отмеченные выше отрицательные явления, но в некоторых случаях служить основным препятствием для повышения производительности машины [2].
(S), будет вызывать динамические нагрузки, которые могут создавать не только отмеченные выше отрицательные явления, но в некоторых случаях служить основным препятствием для повышения производительности машины [2].
Чтобы полностью разгрузить вращательные пары от действия силы ![]() , необходимо установить между игловодителем и стойкой упругой элемент с такой характеристикой Q(S), чтобы она отвечала условию:
, необходимо установить между игловодителем и стойкой упругой элемент с такой характеристикой Q(S), чтобы она отвечала условию:
Q(S) = -![]() (1.4)
(1.4)
при любой частоте вращения кривошипа.
Однако, сила ![]() (1.3) является существенно нелинейной и зависит не только от абсциссы точки В игловодителя, но и от частоты вращения кривошипа. Это создает причины, реализация равенства (1.4) встречает в общем случае значительные конструктивные трудности.
(1.3) является существенно нелинейной и зависит не только от абсциссы точки В игловодителя, но и от частоты вращения кривошипа. Это создает причины, реализация равенства (1.4) встречает в общем случае значительные конструктивные трудности.
При решении этой задачи целесообразно использовать теорию равномерного наилучшего приближения функций в связи с тем, что только такое приближение может гарантировать отклонение функций
Таким образом, поставленная задача состоит в том, чтобы сначала приблизить функцию ![]() полинома:
полинома:
![]() (1.5)
(1.5)
первой степени равномерно и наилучшим образом на отрезке:
![]() (1.6)
(1.6)
а затем определить характеристику Q(S) упругого элемента из условия:
![]() (1.7)
(1.7)
Коэффициенты А и В полинома (1.5) следует подобрать так, чтобы величина имела
![]() (1.8)
(1.8)
минимального значения. Полином Q1(S), дающий минимум величине E1, называют полиномом наилучшего равномерного приближения, или полиномом, мало уклоняющимся от функции Р(S) на отрезке ![]() если,
если,![]()
где: ![]() — постоянная величина, зависящая от структуры и параметров механизма иглы. Тогда из формулы (1.8) следует:
— постоянная величина, зависящая от структуры и параметров механизма иглы. Тогда из формулы (1.8) следует: ![]() , (1.9)
, (1.9)
для всех точек S
Задача по определению ![]() , в данном случае, несколько усложняется с тем, что функция P(S) в явном виде неизвестна. Однако, поскольку функция Р(S) представляет квадратичную функцию, то можно утверждать, что у функции P(S) существует на отрезке (1.6) вторая производная постоянного знака. При этом условии линейная функция (1.5) наилучшего равномерного приближения на отрезке (1.6) будет представлять геометрически среднюю параллель между пересекающей ed, проходящей через крайние точки e и d отрезка параболы и касательной lk к параболе, параллельной этой пересекающихся линий.
, в данном случае, несколько усложняется с тем, что функция P(S) в явном виде неизвестна. Однако, поскольку функция Р(S) представляет квадратичную функцию, то можно утверждать, что у функции P(S) существует на отрезке (1.6) вторая производная постоянного знака. При этом условии линейная функция (1.5) наилучшего равномерного приближения на отрезке (1.6) будет представлять геометрически среднюю параллель между пересекающей ed, проходящей через крайние точки e и d отрезка параболы и касательной lk к параболе, параллельной этой пересекающихся линий.
На рис. 3 функции P(S) и Q1(S) построены в качестве примера для плоского аксиального механизма иглы с геометрическим параметром ![]() = 1/5.
= 1/5.
Величина ![]() будет равна:
будет равна: ![]() (1.10)
(1.10)
где: уе — наибольшая разность между ординатами графиков функций P(S) и Q1(S), показана на рис.3, характеризует абсолютную точность приближения функции ![]() полиномом Q1(S) на отрезке (1.6).
полиномом Q1(S) на отрезке (1.6).
Перейдем теперь к определению функции Q1(S). Уравнение хорды, проходящей через точки d [0,-OA(1+![]() )] и e [20A,OA(1-
)] и e [20A,OA(1-![]() )], графика функции
)], графика функции ![]() определяемой полиномом (1.4), имеет вид (рис. 3):
определяемой полиномом (1.4), имеет вид (рис. 3): ![]() (1.11)
(1.11)
При значении у = 0 (1.11), определяем абсциссу точки q: ![]()
Следовательно, координаты средней точки n1 отрезка eq равны:
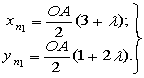 (1.12)
(1.12)
В такой последовательности найдем координаты средней точки п2 отрезка qd:
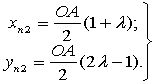 (1.13)
(1.13)
Проведем далее прямую через точки n1 и n2, используя для этого формулы (1.12) и (1.13):
Прямая пересекает ось ординат в точке k(0, — yk,),
где: ![]() (1.15)
(1.15)
а прямую в точке l с координатами: ![]() ,
,
![]()
![]()
![]() (1.16)
(1.16)
В силу известного свойства параболы, прямая (1.14), проходящая через средние точки отрезков eq и qd, обязательно будет касаться параболы. Кроме того, отрезок n1n2 прямой (1.14), являясь средней линией треугольника eqd, будет параллельным пересекающим с edи графика функции ![]() (рис. 3).
(рис. 3).
Отсюда, непосредственно, следует сформулированное выше утверждение о том, что средняя параллель между пресекающей ed и касательной kl к параболе, параллельной этой пересекающейся линии, действительно представляет график линейной функции Q1(S), реализующей наилучшее равномерное приближение к функции P(S) на отрезке (1.6).
Чтобы определить функцию Q1(S) в явном виде, достаточно написать уравнение прямой, проходящей через средние точки s и q отрезков el и kd.
С учётом формулы (1.15) и (1.16), найдем координаты точек s и q:
![]() (1.17)
(1.17)
из уравнения прямой, проходящей через точки (1.17):
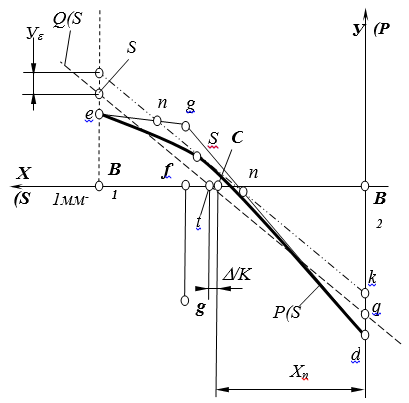
Рис. 3. График изменения силы действия P(S) в зависимости от характеристики Q(S) упругого элемента
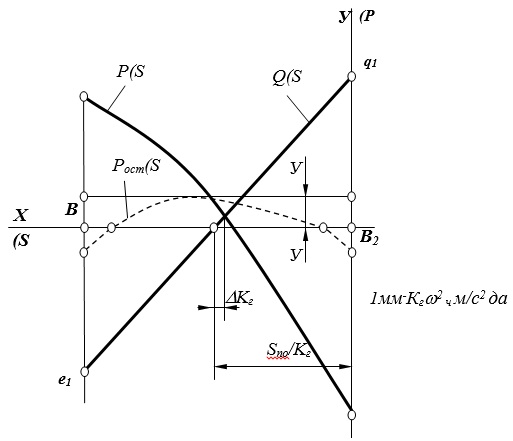
Рис. 4. График дисбаланса силы P(S) и силы Q(S)
![]() Таким образом, коэффициенты полинома (1.5) имеют значения:
Таким образом, коэффициенты полинома (1.5) имеют значения:
![]()
![]() .
.
Заметим, что отклонение Е1 определяемое формулой (1.8), реализуется в трех точках (рис. 3). ![]() где: Sk — абсцисса точки касания параболы с прямой (1.14).
где: Sk — абсцисса точки касания параболы с прямой (1.14).
Подставляя выражение (1.19) в равенство (1.7), получим уравнение характеристики упругого элемента механизма [3].
![]() (1.20)
(1.20)
Из формулы (1.20) найдем жесткость упругого элемента в Н/м:
Параметр Snp упругого элемента, при котором сила Q(S)=0, определяется уравнением:![]() решением, которого получим:
решением, которого получим: ![]() Итак, нулевая точка характеристики упругого элемента смещена относительно точки С на величину
Итак, нулевая точка характеристики упругого элемента смещена относительно точки С на величину ![]() . Таким образом, длина упругой связи в свободном состоянии будет определяться следующим выражением.
. Таким образом, длина упругой связи в свободном состоянии будет определяться следующим выражением.
![]() , (1.22)
, (1.22)
Исходя из вышеизложенного, можно сделать вывод, что снижение динамической нагрузки в кинематических парах механизма иглы способствует повышению надежности и долговечности звеньев, уменьшению частоты колебаний рабочих органов и повышению производительности, с сохранением качества выпускаемых изделий на швейных машинах легкой промышленности.
Литература:
- Рахмонов И. М. Разработка и обоснование параметров механизма иглы с упругим элементом универсальных швейных машин. Дисс. Соискание ученой степени. Канд. техн. Наук. Т.: 2008. 49–59 с.
- Шейно Л. С. Уравновешивание четырехзвенных механизмов. — В кн.: Вестник машиностроения. — М.: 1986. — № 6. — С. 30–33.
- Олимов К. Т. и другие Теоретическое определение сил реакций в шарнирах циклического механизма с упругими элементами // Ж., Проблемы механики. — 2003. — № 6. — С. 26–29.







