Расчет потерь мощности и энергии в кабельной линии при помощи пакетного вейвлет-преобразования



В статье рассмотрена система электроснабжения имеющая нестационарную и нелинейную нагрузку в своём составе. Произведён численный расчет потерь мощности и энергии в кабельной линии электропередач при помощи вейвлет-коэффициентов пакетного вейвлет-преобразования. Полученные при помощи (ПВП) значения потерь энергии сравниваются со значениями полученными по действующим значениям различных гармоник, при заранее известных интервалах времени.

Ключевые слова: пакетное вейвлет-преобразование, вейвлет-коэффициенты, нестационарный режим, высшие гармоники

Рассмотрим систему электроснабжения (СЭС) (Рис 1 а). С линейной нагрузкой Sн и двумя нелинейными нагрузками Sнн1 — вентильный преобразователь (В) (генерирует 5 и 7 гармоники) и Sнн2 — люминесцентные лампы (генерирует 3 и 9 гармоники).

Обычно для расчета режимов СЭС при наличие ВГ применяют принцип наложения. Суть которого состоит в том, что расчет тока в сети производиться отдельно для каждой гармонической составляющей, а затем результаты суммируются. Составим схемы замещения для основной частоты (рис. 1б) и для ВГ (рис. 1в).

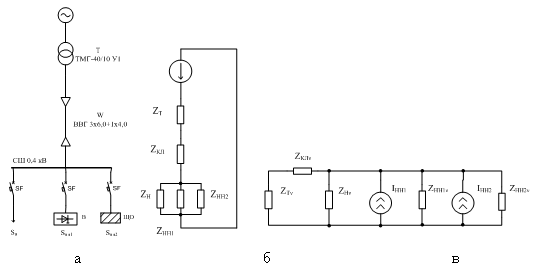
Рис. 1. Система электроснабжения (СЭС) (а), схемы замещения СЭС на основной (б), и высших гармониках (в)

Параметры электрооборудования для расчета режима представлены в таблице 1.

Таблица 1

Паспортные данные трансформатора и кабеля

Трансформатор ТМГ-40/10 У1
Sном, кВА	Uкз, %	Iхх, %		Pхх, кВт	Pкз, кВт		UВН, кВ	UНН, кВ
40	4,7	3		0,17	0,88		10,5	0,38
Кабельная линия ВВГ 3х6,0+1х4,0
r0, Ом/км			x0, Ом/км			Iдл.доп., А
0,443			0,0612			180

Время моделирования режима t=600 c. Представленные на схеме нагрузки имеют различные режимы работы. Отсюда вытекает, что режим будет нестационарный. Весь интервал времени разбиваем на 4 промежутка времени, каждому промежутку времени соответствует различная комбинация нагрузок. Тогда ток для каждого интервала времени может быть записан

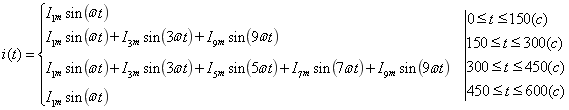(1)

В результате расчета режима данной схемы получены следующие действующие значения токов ВГ (табл. 2).

Таблица 2

Токи кабельной линии на высших гармониках

Токи кабельной линии
I3	I5	I7	I9
13,652+j33,98	22,813+j46,133	23,982+j36,853	6,421+j7,826

В стационарном режиме для расчёта потерь мощности и энергии в токоведущих частях необходимо исходную несинусоидальную кривую разложить на сумму синусоидальных с определёнными значениями амплитуд гармоник и их начальных углов [1, с. 282].

Совокупность амплитуд и фаз образуют дискретные амплитудный и фазовый спектры. Для решения практических задач расчёта потерь в элементах СЭС основное значение имеет амплитудный спектр частот [2, с. 8].

Потери активной мощности в токоведущих частях без учёта эффекта вытеснения тока могут быть определены по формуле:

(2)

В случае дискретных сигналов можно применять также формулу

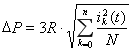(3)

Тогда потери энергии будут равны [4]:

,(4)

Где -квадрат действующего значения тока на ν-той гармонике, R- активное сопротивление кабельной линии.

Главным принципом пакетного вейвлет-разложения является рекурсивное определение последующих элементов более глубокого уровня разложения. Исходный сигнал (в нашем случае ток) домножается на коэффициенты фильтров высоких частот и низких частот, в результате чего получаются детализирующие и аппроксимирующие коэффициенты соответственно. Математически алгоритм, представленный на рисунке 6 можно записать следующими выражениями [4, с. 3 ]:

(5)

(6)

Тогда коэффициенты пакетного вейвлет-преобразования — это результат свертки исходного сигнала на основе вейвлета.

(7)

(8)

Представленная на рисунке 6 схема вейвлет-преобразования предполагает три уровня разложения j= 3.

Действующие значения тока для искомого частотного диапазона с учетом свойств вейвлет-преобразования (5), (6) может быть получено:

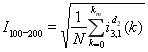.(9)

В результате пакетного вейвлет-разложения получаем матрицы вейвлет коэффициентов (рис. 7), отвечающих за определённые диапазоны частот.

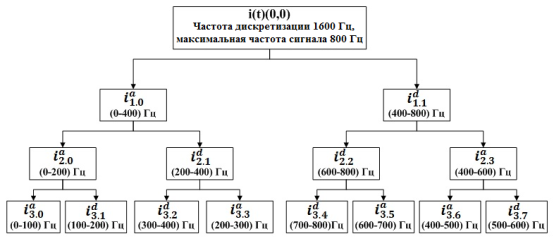
Рис. 6. Блок-схема дерева разложения сигнала

Рис. 7. Вейвлет-спектры коэффициентов

На завершающем этапе работы были рассчитаны потери энергии в кабельной линии на основании вейвлет коэффициентов. Полученные результаты сопоставлялись с потерями, полученными в результате расчета по действующим значениям тока за известный промежуток времени (табл. 3, 4). При этом погрешности в определении потерь очень малы (табл. 5).

Таблица 3

Значения потерь энергии в кабельной линии, рассчитанных отдельно для каждой гармоники по формуле

, кВт·ч	, кВт·ч	, кВт·ч	, кВт·ч	, кВт·ч
583720	89113	88002	64233	68099

Таблица 4

Значения потерь энергии в кабельной линии, рассчитанных отдельно для каждой гармоники, при помощи пакетного вейвлет-преобразования

, кВт·ч	, кВт·ч	, кВт·ч	, кВт·ч	, кВт·ч
583570	89974	87091	64317	67044

Таблица 5

Значения погрешностей при определении потерь энергии

, %	, %	, %	, %	, %
0,026	0,96	1,05	0,13	1,6

Литература:

1. Железко, Ю. С. Потери электроэнергии. Реактивная мощность. Качество электроэнергии: Руководство для практических расчетов / Ю. С. Железко. — М. : ЭНАС, 2009. — 456 с.
2. Жежеленко, И. В. Высшие гармоники в системах электроснабжения промпредприятий / И. В. Жежеленко. — М. : Энергоатомиздат, 2000. — 331 с.
3. Morsi W. G., EI-Hawary M. E. Time-frequency single-phase power components measurements for harmonics and inter-harmonics distortion based on Wavelet Packet transform. Part I: Mathematical formulation // Electrical and Computer Engineering, Canadian Journal, Vol. 35, Winter 2010. — P. 1–7.