Решение транспортных задач с помощью линейного программирования



Одним из путей сокрушения затрат на доставку грузов является правильный подбор авто средств (АТС) в соответствии с условиями их работы и особенностями перевозимых грузов.

Задача выбора оптимального комплекта АТС в общем виде формулируется следующим образом.

В течении определенного промежутка времени нужно осуществить перевозку Sгрупп грузов. Общая масса грузов каждой группы равна w_i(i=1.2….,5). Известно расстояние перевозки каждой группы e_i. Для доставки грузов могут быть использованы АТС различных моделей. Общее число моделей равно n, a максимально возможное число машин каждой модели –N_jmax(j=1,2,…n).

Необходимо распределить АТС по группам таким образом, чтобы обеспечивалась своевременная доставка всего объема грузов каждой группы, а эффективность работы выбранного комплекта машин была бы наибольшей.

Для выполнения первого условия необходимо чтобы общая производительность АТС выбранных для перевозки грузов i-й группы, была больше или равен общему объему грузов этой группы:

(1)

где Q_ij — производительность АТС j–й модели на доставке грузов i-й группы, Т/год;

X_ij-число единиц АТСj-й модели занятых доставкой грузов i-й группы. Второе условие выполняется, если

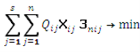(2)

где p-приведенные затраты на доставку грузов i-й группы автотранспортными средством j- й модели сум/Т рассчитываемые по выражению

З_ijn=Ц_jE_n/Q_ij+C_ij, сум/Т(3)

где Ц — балансовая стоимость АТС j-й модели, сум; E_n — нормативный коэффициент; C_ij -себестоимость доставки 1т груза i-й группы на АТС j — й модели, сум/ T

Формула(2) является критерием оптимизации комплекта АТС. Его переменные величины X_ij должны отвечать следующим ограничениям:

(4)

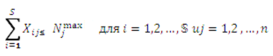2)(5)

Указанная выше задача в описанной постановке решается методом линейного программирования с использованием ЭВМ. При решение ряда практических задач по выбору оптимального комплекта АТС ограничения на число машин могут отсутствовать. В этом случае задача может быть решена без применения аппарата линейного программирования и сводится к выбору оптимальной модели АТС для доставки каждой отдельной группы грузов, т. е. для доставки грузов i- й группы необходимо использовать такую модель АТС, у которой

З_nij→min при j = 1,2.,….,n. (6)

Потребное число АТС каждой f-й группы оптимальной модели определяется как

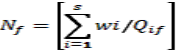
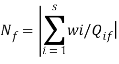,(7)

где знак означает ближайшее большее число по сравнению с числом, полученным в результате суммирования (например, если сумма равна -1,5,то берётся число 2).

Для выбора оптимальных моделей АТС по критерию (6) необходимо рассчитать значения

З_nij для i=1,2,…..,s Ц j=1,2,…,n

(это же необходимо сделать и при расчетах по критерию (2)). Формулу (3) для расчёта З _nij после подстановки отдельных статей себестоимости транспортной работы С_nij преобразования можно представить в виде

З_nij= (8)

где а _j, b_j u d_j -постоянные коэффициенты, зависимые от нормативов отдельных статей эксплуатационных затрат, а также от технико-эксплуатационных показателей АТС (грузоподъемность, стоимость и другие).

Анализ формулы (8) показывает, что она имеет определённую погрешность, обусловленную тем, что обьем перевозок i-й группы, приходящийся на одну машину j-го типа из оптимального комплекта, равный W_i/X_ij, в общем случае не равен возможной производительность Q_ij в связи с округлением при определении числа АТС. Причём разность между величинами W_i/X_ijQ_ij будет больше при меньших значениях X_ij

Определим возможную погрешность, получаемую при определении З _nij в результате использования в формуле (8) величины Q_ij вместо w_i/X_ij. Для этого заменим в этой формуле на Q_ij К_исп /., где К_исп –коэффициент, учитывающий расхождение между величинами Q_ij и W_i /X_ij:

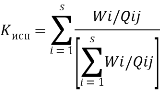(9)

В результате получим уточненное значение

Зⁱ_nij=К_исп (10)

Относительная ошибка в значениях Зn_ij и Зn_ij равна

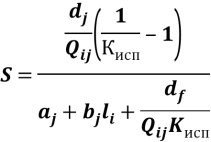(11)

Приведённые расчёты показали, что для ряда АТС для перевозки грузов величины являются такими, что с учётом возможного значения К_исп (до 0,6) значение погрешности может достигать до 25 %.

Все это говорит о том, что использование значения Q_ij в формуле (8) при определении оптимального комплекта в ряде случаев может привести к ошибочным результатам и выводам. С другой стороны использование в этой формуле значения w_i/ X_ij не возможно, так как величинa X_ij заранее не известна.

В связи с этим предлагается следующий метод выбора оптимального комплекта АТС, учитывающий возможные погрешности.

1. По критерию (6) определяются модели АТС, являющиеся оптимальными для грузов каждой группы (предварительный оптимальный набор машин).
2. Для каждой модели из предварительного оптимального набора определяется потребность по формуле (7) и коэффициент К_исп. по (9), а затем по (10) –значение З_nij применительно к доставке грузов в соответствующих групп.
3. В каждой группе грузов устанавливаются модели, значение З_nij для которых меньше, чем величина З _nij соответствующей оптимальной модели, найденная на этапе 2.

Если во всех группах грузов такие модели отсутствуют, оптимальный комплект, найденный выше, принимается в качестве окончательного. В противном случае должна проводиться проверка оптимальности этого комплекта следующим образом.

4. Модели АТС, установленные на этапе 3, совместно с моделями предварительного оптимального набора, группируются в каждой группе грузов, например в виде таблицы.

Группa грузов
1	2	3	4	5
С	A	Д	Д	Е
A		A

Примечание. А; С; Д; Е — условные обозначения моделей машин.

Модели АТС, приведенные в таблице, представляют собой совокупность возможных оптимальных моделей для рассматриваемого условного примера.

Для указанной совокупности выписываются все возможные наборы машин:

САДДЕ; ААДДЕ;АААДЕ;СААДЕ.

5.Для каждого из а полученных наборов последовательно определяются значения применительно к грузам каждой группы.

6.Для всех наборов машин находится величина

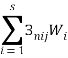
Набор АТС, у которого величина является минимальной, принимается в качестве окончательного оптимального набора машин. Для этого набора устанавливается число АТС каждой модели, определённое ранее, т.е находится оптимальный комплект АТС.

Выводы: В общем случае задача выбора оптимального комплекта АТС решается с использованием методов линейного программирования.

При отсутствии ограничений на число АТС задача сводится к выбору оптимальной модели АТС для доставки грузов каждой отдельной группы по критерию (6).

В случаях, когда потребность в АТС любой из моделей оптимального комплекта, найденного по критерию (6), не превышает 7–8, должна проводиться проверка оптимальности этого комплекта и при необходимости выбор нового комплекта по методике, предложенной в настоящей работе.