Ключевые слова: печь сопротивления, производство карбида кремния, математическая модель, температурное поля, тепломассоперенос.
Одним из приоритетных направлений эффективного использования энергетических ресурсов в условиях производства является оптимизация технологического процесса.
Современным способом всестороннего изучения и оптимизации параметров промышленных объектов является математическое моделирование. Математическая модель — это уравнение или система уравнений, связывающих параметры процесса с факторами, влияющими на них. При этом факторы являются зависимыми переменными. Обычно существует также взаимная связь как между параметрами, так и между некоторыми факторами [1]. Комплексное моделирование способно решить задачи повышения энергоэффективности. Также моделирование позволяет избегать производственных экспериментов, что связано с экономией исходных материалов и потребления электроэнергии.
Рассмотрим процесс производства карбида кремния (SiC). Электрическая печь для производства карбида кремния относится к типу электропечи сопротивления. Конструкция боковых стенок печи изображенной на рис.1 имеет отверстия для выхода наружу образующихся в печи газов и последующего горения их вне печи.
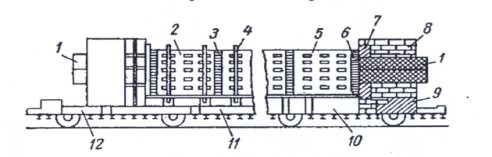
Рис. 1. Самоходная печь для производства карбида кремния: 1 — токоподводящие электроды; 2 — боковой щит передней стенки; 3 — кирпичная кладка; 4 — стойка для крепления боковых щитов; 5 — боковой щит задней стенки; 6 — контактный материал из графитированных отсевов; 7 — защитные электроды; 8 — торцовая стенка из огнеупорного кирпича; 9 — бетонный корпус торца; 10 и 12 — тележки концевые; 11 — тележка средняя
Карбид кремния в промышленных условиях получают восстановлением кремнезема углеродистым материалом. Протекающие при этом химические реакции можно представить брутто-уравнением
SiO2 + 3C = SiC + 2CO
Процесс получения SiC осуществляют в специальных электрических печах [2, 3], в которых разогрев исходных продуктов до необходимой температуры проводится электрическим током.
Реакция начинается при температуре около 1500 °С и протекает с поглощением энергии. В условиях неравномерности температур, которая всегда имеет место в печах для получения карбида кремния, химические реакции протекают в несколько стадий. Сначала образуется оксид кремния по реакции
SiO2 + C = SiО + CO.
Вступая в реакцию с углеродом, оксид кремния частично преобразуется непосредственно в карбид кремния по реакции
SiO +2C = SiС + CO,
а частично восстанавливается до кремния
SiO + C = Si + CO.
Пары кремния затем реагируют с углеродом с образованием конечного продукта:
Si + C = SiС.
Основным сырьем для производства карбида кремния служат кварцевый песок и нефтяной кокс. К сырьевым материалам предъявляются высокие требования по чистоте, так как большое содержание примесей (оксиды АI2O3, Fe2O3, СаО) снижает качество и выход годного карбида кремния. Кроме основных сырьевых материалов в реакционную шихту при загрузке печи добавляются возвратные материалы, полученные после электротермического процесса, — возвратная шихта и возвратный аморф. Возвратная шихта представляет собой смесь кварцевого песка, прокаленного нефтяного кокса и карбида кремния. Возвратный аморф — мелкокристаллический карбид кремния, полученный после сортировки куска карбида кремния [2].
Карбид кремния и остальные продукты плавки располагаются концентрическими слоями вокруг керна (рис. 2). За керном располагается слой графита, далее следует сам карбид кремния, а после него слои аморфа и силоксикона, т. е. непрореагировавшие с достаточной интенсивностью слои.
Карбид кремния (КК) выпускается промышленностью в виде двух разновидностей, отличающихся друг от друга цветом (КК зеленый (КЗ) и КК черный (КЧ)), качеством и технологией производства.
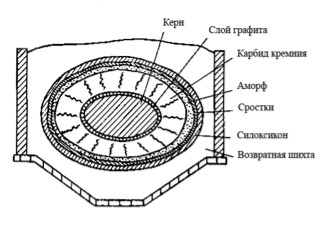
Рис. 2. Разрез печи по окончании плавки
Кроме вышеперечисленных сырьевых материалов при производстве зеленого карбида кремния в шихтовые материалы добавляется хлорид натрия и опилки. При производстве электротехнического карбида кремния в шихту добавляют глинозем.
В связи с тем, что процессы, протекающие в нагревательных печах, весьма энергоёмки, актуальным является проведение политики энергосбережения и повышение эффективности работы печей.
Немногие известные математические модели процесса производства карбида кремния используют существенно упрощенную картину процесса и не позволяют получить необходимую информацию об изменении важных для получения карбида кремния параметров, определяющих его качество и выход как конечного продукта производства.
Математическая модель производства карбида кремния должна состоять из системы уравнений, характеризующих технически и организационно обоснованные условия и показатели печи.
Математическое моделирование позволяет сократить энергопотребление за счёт устранения избыточного расхода энергии и реализации энергосберегающих мероприятий [4]:
- Повышение производительности печи.
- Снижение тепловых потерь.
- Оптимизации процесса плавки [5].
- Использование теплоты отходящих газов.
- Автоматизация работы печи.
Для получения полного математического описания необходимо провести анализ химических и физических процессов, протекающих в электрических печах, для выявления базовых факторов, которые необходимо учитывать при математическом моделировании для воспроизведения поля температур в рабочей зоне печи [6–11].
Представим упрощенную математическую модель для расчета температурного поля в печи сопротивления, которая состоит из двумерного дифференциального уравнения теплопроводности с внутренними источниками теплоты, представленного в виде:
![]() (1)
(1)
где Т– температура, τ — время, λ — коэффициент теплопроводности,![]() — мощность внутренних источников тепла в теле.
— мощность внутренних источников тепла в теле.
Причём мощность внутренних источников является комплексным параметром, состоящим из нескольких слагаемых, зависящих от большого количества величин.
Граничные условия, используемые для решения уравнения имеют следующий вид:
Начальные условия:
τ = 0: Т = Т0 = 300 К, P= P0 = 105 Па.
Все начальные параметры не зависят от координат.
Граничные условия при τ > 0:
X = 0, 0 ≤ Y ≤ 1; Y = 0, 0 ≤ X ≤ 1: ![]()
X = l, 0 ≤ Y ≤ 1; Y = l, 0 ≤ X ≤ 1: ![]()
где Tc — температура поверхностей стенок плавильной печи; Тж — температура окружающей среды; α — эквивалентные коэффициенты теплоотдачи, учитывающие особенности расположения поверхностей.
Для подтверждения работоспособности предложенной упрощенной модели процессов тепломассообмена необходимо провести ряд численных экспериментов. Результаты численных вариантов температурных кривых сравнить с известными данными из литературных источников. И по результатам численных экспериментов предложить возможные варианты оптимизации процесса производства карбида кремния в печах сопротивления.
Литература:
1. Егоров А. В. Расчет мощности и параметров электроплавильных печей: Учебное пособие для вузов. М.: МИСИС, 2000. 272 с.
2. Полубелова А. С., Крылов В. Н., Карлин В. В., Ефимова И. С. Производство абразивных материалов. — СПб.: Машиностроение, 1968. — 180 с.
3. Марковский Л. Я., Оршанский Д. Л., Прянишников В. П. Химическая электротермия. – Ленинград: Государственное научно-техническое издательство химической литературы, 1952. — 408 с.
4. Закожурников Г. С., Гаряев А. Б. Оценка потенциала энергосбережения в технологическом процессе плавки карбида кремния // Седьмая международная школа-семинар молодых учёных и специалистов Энергосбережение теория и практика, г. Москва, 13–17 октября 2014 г.
5. Кузеванов В. С., Закожурников С. С., Гаряев А. Б. Оптимизация процесса плавки карбида кремния с целью повышения её производительности и снижения расхода электроэнергии// Промышленная энергетика. — 2015. — № 6. — С. 29–33
6. Кузеванов В. С., Закожурникова Г. С., Закожурников С. С. Модель тепломассопереноса в печах при производстве карбида кремния // Альтернативная энергетика и экология. — 2015. — № 7. — С. 75–81.
7. Кузеванов В. С., Закожурникова Г. С. Модель сушки пористого проницаемого материала при внутреннем нагреве // Альтернативная энергетика и экология. — 2013. — № 14. — С. 19–23.
8. Кузеванов В. С., Закожурникова Г. С. Модель сушки пористого проницаемого материала при внутреннем нагреве // Письма в Международный научный журнал «Альтернативная энергетика и экология». — 2014. — № 3 (4). — С. 37–38.
9. Кузеванов В. С., Закожурникова Г. С. Общая модель для расчета поля давления в пористой среде с реагирующими компонентами // Известия ВолгГТУ. Серия Процессы преобразования энергии и энергетические установки. — 2014. –Т. 18 № 6 (145)– С. 106–110.
10. Кузеванов В. С., Закожурникова Г. С. Расчет поля давления в пористой среде с реагирующими компонентами // Известия ВолгГТУ. Серия Процессы преобразования энергии и энергетические установки. — 2014. — Т. 18 № 6 (145)– С. 110–113.
11. Закожурникова Г. С. Расчет поля давления в пористой среде с реагирующими компонентами / Материалы докладов X Международной молодежной научной конференции «Тинчуринские чтения» 25–27 марта 2015. В 3 т. — Казань: Казан. гос. энерг. ун-т, 2015. — Т.2. — С. 33–34.







