В 1967 году американские учёные К.С. Гарднер, Дж.М.Грин, М.Крускал и Р.Миура [1] открыли замечательное свойство уравнения Кортевега-де Фриза (КдФ). Они предложили нелинейную замену переменных в этом уравнении, после которой оно становится линейным и явно решается. В описании этой замены участвует формализм прямой и обратной задач рассеяния для оператора Штурма-Лиувилля, т.е. в нем существенно используется решение задачи о восстановлении потенциала оператора Штурма-Лиувилля на всей оси, по данным рассеяния. Этот метод получил название метода обратной задачи рассеяния. В работе [2] П.Лакс показал, универсальность метода обратной задачи рассеяния и обобщил уравнение КдФ, введя понятие высшего (общего) уравнения КдФ. Затем МОЗР был успешно применен и для многих других нелинейных эволюционных дифференциальных уравнений, таких как: нелинейное уравнение Шредингера, модифицированное уравнение Кортевега-де Фриза, уравнение sin-Гордон.
Рассмотрим линейную систему уравнений
![]() (1)
(1)
на всей оси (![]() ), с «быстроубывающим» потенциалом
), с «быстроубывающим» потенциалом ![]() :
:
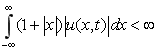 .(2)
.(2)
Здесь 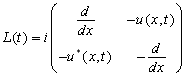 ,
, ![]() является комплексным сопряжением к
является комплексным сопряжением к ![]() .
.
Прямая и обратная задача рассеяния для оператора ![]() изучены в работах М.Г.Гасымова, Б.М.Левитана [3], В.Е.Захарова, А.Б.Шабата [4], И.С.Фролова [5], Л.П.Нижника, Фам Лой Ву [6], Л.А.Тахтаджяна, Л.Д.Фаддеева [7], А.Б.Хасанова [8] и др.
изучены в работах М.Г.Гасымова, Б.М.Левитана [3], В.Е.Захарова, А.Б.Шабата [4], И.С.Фролова [5], Л.П.Нижника, Фам Лой Ву [6], Л.А.Тахтаджяна, Л.Д.Фаддеева [7], А.Б.Хасанова [8] и др.
В данной работе рассматривается система уравнений
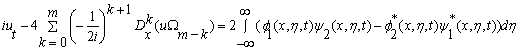 , (3)
, (3)
![]() , (5)
, (5)
при начальном условии
![]() ,(6)
,(6)
где ![]() определяется из следующих реккурентных соотношений
определяется из следующих реккурентных соотношений
![]() ,
, 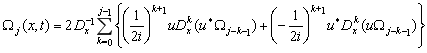 ,
, ![]() .
.
Здесь начальная функция ![]()
![]() обладает следующими свойствами:
обладает следующими свойствами:
1) ![]() (7)
(7)
2) Оператор ![]() не имеет спектральных особенностей и в верхней полуплоскости комплексной плоскости имеет ровно N собственных значений
не имеет спектральных особенностей и в верхней полуплоскости комплексной плоскости имеет ровно N собственных значений ![]() с кратностями
с кратностями ![]() .
.
В рассматриваемой задаче вектор-функции ![]() и
и ![]() решения системы уравнений
решения системы уравнений ![]() и
и ![]() соответственно, которые обладают следующими асимптотиками при
соответственно, которые обладают следующими асимптотиками при ![]()
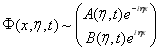 ,
, 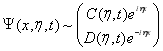 ,(8)
,(8)
где
![]() при
при ![]() .(9)
.(9)
Предполагается, что при всех ![]()
![]() (10)
(10)
Пусть функция ![]() обладает достаточной гладкостью, т.е.
обладает достаточной гладкостью, т.е. ![]() и достаточно быстро стремится к своим пределам при
и достаточно быстро стремится к своим пределам при ![]() , так что
, так что
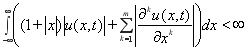 .(11)
.(11)
Основная цель данного работы – получить эволюции данных рассеяния несамосопряженного оператора ![]() с потенциалом являющимся решением уравнения (3).
с потенциалом являющимся решением уравнения (3).
Допустим, что решение ![]() задачи (3)-(11) существует. Рассмотрим систему уравнений
задачи (3)-(11) существует. Рассмотрим систему уравнений
![]() (12)
(12)
с потенциалом ![]() . Пусть вектор-функции
. Пусть вектор-функции ![]() и
и ![]() решения уравнений
решения уравнений ![]() и
и ![]() соответственно с асимптотиками (8) при
соответственно с асимптотиками (8) при ![]() . С помощью решений Йоста
. С помощью решений Йоста ![]() и
и ![]() уравнений (12), определим вектор-функции
уравнений (12), определим вектор-функции
![]()
![]()
![]() .(14)
.(14)
Здесь 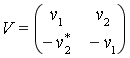 и
и ![]() ,
,
![]() .
.
По определению, вектор-функции ![]() и
и ![]() аналитические функции от параметра
аналитические функции от параметра ![]() в верхней полуплоскости
в верхней полуплоскости ![]() . При любых действительных
. При любых действительных ![]() вектор-функции
вектор-функции ![]() и
и ![]() имеют особенности в точке
имеют особенности в точке ![]() . Чтобы определить предельные значение вектор-функций
. Чтобы определить предельные значение вектор-функций ![]() и
и ![]() при
при ![]() , используем формулы Сохоцкого. В силу (13), (14) имеем
, используем формулы Сохоцкого. В силу (13), (14) имеем
![]()
![]()
![]() ,(15)
,(15)
![]()
![]()
Здесь v.p. означает, что интеграл понимается в смысле главного значения.
Согласно (8) имеем
![]() ,
,
![]() ,
,
поэтому при ![]() :
:
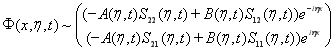 ,(17)
,(17)
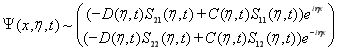 .(18)
.(18)
Нетрудно заметить, что справедливы равенства
![]() .
.
Следовательно, ![]() и
и ![]() линейно зависимы с
линейно зависимы с ![]() и
и ![]() соответственно, т.е. существуют такие
соответственно, т.е. существуют такие ![]() и
и ![]() , что имеют место соотношения
, что имеют место соотношения
![]() . (20)
. (20)
По определению матрицы ![]() , из равенств (10) и асимптотик (8), (17) и (18), получим
, из равенств (10) и асимптотик (8), (17) и (18), получим
![]()
![]()
![]() ,
,
где ![]() .
.
Введем следующее обозначение
![]() .
.
На основании равенств (19), (20) вектор ![]() можно переписать в виде
можно переписать в виде
![]()
![]() .(21)
.(21)
С другой стороны, из соотношений (15) и (16) имеем
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Используя равенство ![]() получим
получим
![]() . (22)
. (22)
Сравнивая равенства (21) и (22) имеем
![]() (23)
(23)
![]() ,
,
следовательно
![]() .
.
Заметим, что дифференциальное уравнение (23) справедливо при ![]() . Легко заметить, что при
. Легко заметить, что при ![]() справедливо равенство
справедливо равенство
![]() .(24)
.(24)
Решая дифференциальное уравнение (24) получим
Отсюда следует, что нули ![]() функции
функции ![]() , т.е. собственные значения оператора
, т.е. собственные значения оператора ![]() не зависят от
не зависят от ![]() .
.
Перейдем к нахождению эволюции нормировочной цепочки ![]() соответствующей
соответствующей ![]() кратным собственным значениям
кратным собственным значениям ![]()
Заметим, что при ![]() справедливы равенства
справедливы равенства
![]() , (25)
, (25)
![]() .(26)
.(26)
Теперь определим функцию ![]() в виде
в виде
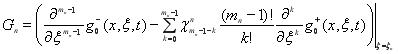 .
.
В силу равенств (25) и (26) имеем
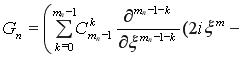
![]()
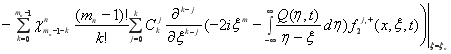 . (27)
. (27)
Равенство (27) можно переписать в виде
![]()
![]()
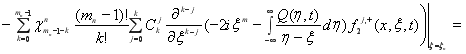
![]() ,(28)
,(28)
где 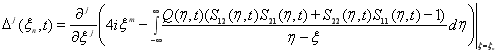 ,
,
Следовательно, согласно ![]()
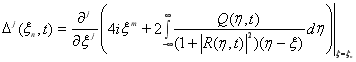 .
.
С другой стороны, на основании равенств (13) и (14) имеем
![]()
![]()
![]()
![]() .(29)
.(29)
Сравнивая равенства (28) и (29), получим
![]() ,
, ![]()
Таким образом доказана следующая
Теорема. Если функции ![]() являются решением задачи (3)-(11), то данные рассеяния несамосопряженного оператора
являются решением задачи (3)-(11), то данные рассеяния несамосопряженного оператора ![]() с потенциалом
с потенциалом ![]() меняются по
меняются по ![]() следующим образом
следующим образом
![]() ,
,
![]()
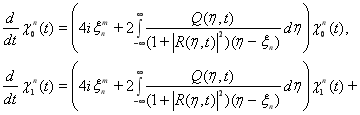
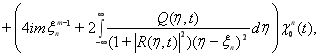
![]() ,
, ![]()
Полученные равенства полностью определяют эволюцию данных рассеяния, что позволяет применить метод обратной задачи рассеяния для решения задачи (3)-(11).
Литература:
- Gardner C.S., Сreen I.M., Kruskal M.D., Miura R.M. Method for solving the Korteweg-de Vries equation // Phys. Rev. Lett. – USA, 1967. – v.19 – p. 1095-1097.
- Lax P.D. Integrals of nonlinear equations of evolution and solitary waves // Comm. Pure and Appl. Math. – USA, 1968. – v.21. – p. 467-490.
- Гасымов М.Г., Левитан Б.М. Обратная задача для системы Дирака // ДАН СССР. – Москва, 1966. – Т.167, № 5. – C. 967-970.
- Захаров В.Е., Шабат А.Б. Точная теория двумерной самофокусировки и одномерной автомодуляции волн в нелинейной среде // ЖЭТФ. – Москва, 1971. – Т.61. № 1. – C.118-134.
- Фролов И.С. Обратная задача рассеяния для системы Дирака на всей оси // ДАН СССР. – Москва, 1972. – Т.207, № 1. – С.44-47.
- Нижник Л.П., Фам Лой Ву. Обратная задача рассеяния на полуоси с несамосопряженной потенциальной матрицей // Укр. матем. журнал. – Киев, 1974. – Т.26, № 4. – С.469-486.
- Тахтаджян Л.А., Фаддеев Л.Д. Гамильтонов подход в теории солитонов.–/ М.:, Наука. 1986. – 528 с.
- Хасанов А.Б. Об обратной задаче теории рассеяния для системы двух несамосопряженных дифференциальных уравнений первого порядка // ДАН СССР – Москва, 1984. – Т.277, № 3. – C. 559-562.
- Хасанов А.Б., Рейимберганов A.A. Конечно плотные решения высшего нелинейного уравнения Шредингера с самосогласованным источником // Уфимский матем. журнал. – Уфа 2009, том 1. № 4. – С. 133-143.







