Разработка пакета прикладных программ, что особенно актуально в рамках математической физики, является очень важной. Это означает, в первую очередь, необходимость, модельного анализа рассматриваемого класса задач. При этом выделяются отдельные подзадачи математических моделей, выполнение которых в различных комбинациях обеспечивает решение всех планируемых задач.
Ключевые слова: пакет прикладных программ, эллиптические, параболические, гиперболические, линейные задачи, нелинейные задачи, краевые условия, смещенные условия, сеточные методы, сеточные функции, сеточные операторы, итерационные методы.
Многообразие задач математической физики кажется необозримым, если представить возможную их классификацию по различным критериям, существенным как с алгоритмической, так и с программисткой точек зрения. Прежде всего, исходная математическая постановка определяется следующим категориями:
- тип дифференциальных уравнений (эллиптические, параболические, гиперболические, а также системы уравнений, в том числе разных типов);
- вид коэффициентов (постоянные, линейные или нелинейные, т. е. зависящие от решения);
- размерность области (одно-, двух-, или трёхмерная);
- конфигурация границы (на примере двухмерных задач): прямоугольная, составленная из прямоугольников, криволинейная односвязная или многосвязная, ограниченная или открытая и т. д.;
- тип краевых условий 1, 2 или 3-го рода, смешанные условия, свободные границы, условия сопряжения на внутренних поверхностях.
Сеточные методы градации также по достаточно большому числу характеристик: принцип аппроксимации (методы конечных элементов, конечно-разностные или интегро-интерполяционные схемы, методы коллокаций); тип сеток (равномерные или неравномерные, регулярные или не регулярные, треугольные, четырехугольные и т. д.); вид сеточных шаблонов, т. е. совокупности узлов, участвующих в отдельных уравнениях; способ построения сеточных уравнений (на одинаковых шаблонах можно получить различные аппроксимационные выражения); методы решения сеточных уравнений (явные или неявные, одношаговые или многошаговые, прямые или итерационные и т. д.). Тем не менее сеточные методы решения различных задач математической физики допускают формализованное единообразное представление, которое можно далее детализировать до любого желаемого уровня.
Решение дифференциальных уравнений сеточными методами есть задача вычисления приближенных значений функций ![]() в узлах
в узлах ![]() ; для различных моментов времени
; для различных моментов времени ![]() . Исходная дифференциальная задача аппроксимируется системой сеточных уравнений, которую можно записать в виде:
. Исходная дифференциальная задача аппроксимируется системой сеточных уравнений, которую можно записать в виде:
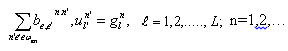 (1)
(1)
где ![]() — совокупность номеров узлов, составляющих сеточный шаблон для
— совокупность номеров узлов, составляющих сеточный шаблон для ![]() -го узла в момент
-го узла в момент ![]() , на величины
, на величины ![]() задаются значениями коэффициентов и свободных членов дифференциальных уравнений, расстояний между «соседними» (входящими в один шаблон) узлами, а также видом краевых и начальных условий. Для стационарных задач индекс
задаются значениями коэффициентов и свободных членов дифференциальных уравнений, расстояний между «соседними» (входящими в один шаблон) узлами, а также видом краевых и начальных условий. Для стационарных задач индекс ![]() везде опускается.
везде опускается.
Обозначая совокупность значений сеточных функций для моментов времени ![]() через векторы
через векторы ![]() , решение сеточных уравнений можно свести к вычислению последовательностей:
, решение сеточных уравнений можно свести к вычислению последовательностей:
![]() (2)
(2)
где ![]() — известные, а
— известные, а ![]() — искомые сеточные функции;
— искомые сеточные функции; ![]() — сеточные операторы (матрицы), которые могут быть заранее вычислены или определяются значениями
— сеточные операторы (матрицы), которые могут быть заранее вычислены или определяются значениями ![]() (нелинейные задачи). В стационарних задачах сеточные функции также вычисляются по формулам вида (2), но n здесь означает, как правило, номер итерации. [2]
(нелинейные задачи). В стационарних задачах сеточные функции также вычисляются по формулам вида (2), но n здесь означает, как правило, номер итерации. [2]
Сеточные методы в форме (2) называются явными, если
Рекуррентная последовательность (2) внешне выглядит двучленной, но в таком виде можно представить и многочленные последовательности. Так, соотношение:
![]() (3)
(3)
которое возникает при решении волновых уравнений, можно записать в форме (2), если определить:
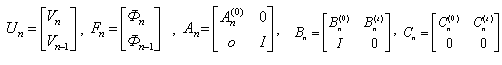
Где ![]() — единичный оператор.
— единичный оператор.
Если исходная задача представляет собой систему дифференциальных уравнений, то ![]() является сеточной вектор-функцией. Например, система:
является сеточной вектор-функцией. Например, система:
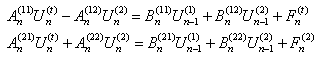 (4)
(4)
Сводится к (2) при введении обозначения:
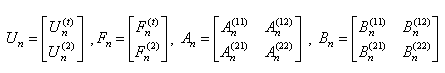
Во многих практических задачах требуется не просто найти решение при заданных граничных и начальных условиях, а исследовать зависимость решения от исходных параметров или же искать оптимальные значения этих параметров, при которых решение будет обладать некоторыми заданными свойствами (т. е. решается задача минимизацией какого-либо функционала). Это приводит к многократному расчету различных вариантов с обработкой и анализом промежуточных результатов.
Решение задач математической физики и возникающие при этом технологические вопросы разработки алгоритмов и ППП можно представить с помощью следующих основных этапов:
- Подготовка исходных данных. Сюда включается описание типа дифференциального уравнения (или системы уравнений), вида его коэффициентов, конфигурации расчетной области, граничных условий и начальных данных. Для задач оптимизации дополнительно указываются варьируемые параметры их ограничения и целевая функция (минимизируем функционал). Когда пакет программ предусматривает возможность использования различных методов, задание может содержать описание нужных алгоритмов или их счётный параметров (тип сетки, количество узлов, вид сеточных уравнений, метод их решения и т. д.). Наконец сюда же могут включаться требования к содержанию и форме представляемых пользователю результатов или сообщений о ходе вычислительного процесса.
Если ППП рассчитан на узкий класс задач, например, на решение конкретной системы уравнений и областях простой формы с помощью фиксированного набора алгоритмов, то структура входных данных, как правило, проста, и для их ввода достаточно средств алгоритмических языков; трудности могут состоять только в большом объеме числовых массивов. Однако для универсальных пакетов, ориентированных на пользователей-специалистов в своих проблемных областях (но не программировании), эффективность эксплуатации определяется в значительной степени наличием специализированного входного языка, наглядностью и развитостью его средств. Так, в двумерных, и трехмерных задачах с границей сложной конфигурации имеет самостоятельное значение проблема автоматизации описания краевых задач [1].
- Дискретизация дифференциальной задачи. Данный этап заключается в построении сетки и формировании сеточных уравнений; аппроксимация дифференциальных уравнений и краевых условий, формирование матрица вида An, Bn, Cn векторов Fn. Эти проблемы легко реализуются для областей простой формы (прямоугольник, параллелепипед) и достаточно гладких решений, когда вполне удовлетворительными являются равномерные прямоугольные сетки и простейшие способы аппроксимации. Однако при наличии криволинейной границы посторенние сетки, например триангуляция области в методе конечных элементов, представляет собой нетривиальную математическую задачу, требует трудоемкого тщательного учета ее специфики и контроля качества сетки. В подобластях с резким изменением решения сетка должна быть гуще, углы между линиями — не меньше определенной величины и т. д. В окрестностях особых точек (углы границы, смена краевых условий или скачки коэффициентов уравнения) аппроксимации должны строиться с учетом локального поведения решения. Проблема определения оптимальных или автоматизация построения «хороших» сеток в общем случае не решена. И вряд ли может быть полностью формализована. Построения сеток по видимому, надо проводить на основе анализа априорной информации о задаче или предварительного грубого приближения к решению. Более того, некоторых нестационарных задачах неизбежно применение сеток, меняющихся со временем.
В многомерных задачах актуальным является вопрос с способе представления и хранения элементов сеточных операторов и функций: решение его может быть различным на разных ЭВМ поскольку здесь имеет большое значение соотношение объема оперативной памяти и скорости вычислений.
Видимо бессмысленно говорить о возможности построения единого алгоритма дискретизации на всем случаи жизни однако модульный принцип позволяет в этом многообразии вопросов выделить фрагменты методов эффективно реализующие отдельные особенности задачи и путем их различных сочетаний обеспечить достаточно экономичное решение широкого класса задач.
-
Решение сеточных уравнений. В нестационарных задачах решение сводится к вычислению в сеточных функциях для последовательности временных интервалов в стационарных-применяются или итерационные или прямые методы решения алгебраических уравнений, которые имеют ярко выражению специфику в силу ленточной структуры формируемых матриц. Применение методов типа Гаусса или Холесского достаточно экономичны, но требуют запоминания больших числовых массивов. Например, при решении уравнения Пуассона в кубе на сетке с числом узлов N*N*N при простейшей семиточечной аппроксимации нужно хранить примерно
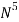 элементов матриц. Для больших
элементов матриц. Для больших 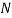 реализация таких методов возможна лишь при интенсивном использовании внешней памяти, что не только существенно увеличивает время счета, но и усложняет структуру программы.
реализация таких методов возможна лишь при интенсивном использовании внешней памяти, что не только существенно увеличивает время счета, но и усложняет структуру программы.
Итерационные алгоритмы (методы верхней релаксации или переменных направлений с приемами ускорения сходимости) легко реализуются в пакетах программ и для многих практических задач дают хорошие результаты. Решение становится «дорогим», если коэффициенты дифференциальных уравнений сильно отличаются в области по абсолютной величине или по соображениям точности сетки приходится строить с большим числом узлов и сильно неравномерными шагами.
Современные эффективные подходы к решению сеточных задач основаны на комбинации прямых и итерационных методов. Эффективными являются подходы типа альтернирующего метода Шварца, когда расчетная область разбивается на подобласть с поочередным вычислением последовательных приближений к решению в каждой из них. При использовании в простых подобластях равномерных сеток особенно экономичны методы быстрого преобразования Фуре, или циклической редукции. Особо следует отметить возможность существенного выигрыша за счет применения последовательности сеток. Сначала приближенное решение ищется на вспомогательных редких сетках, затем производится интерполяция в узлы густой сетки, и на ней далее решения уточняется при этом можно добиться значительного сокращения объеме вычислений, а путем комбинирования решения на разных сетках повысить порядок точности (известная экстраполяция Ричардсона).
Надо отметить, что формирование состава модулей необходимо проводить с учетом чисто программистских особенностей. Например напрашивается объявить модулем процедуру реализации метода прогонки и использовать ее в различных многомерных задачах. Однако если процедура рассчитана на переменные коэффициенты системы трехточечных уравнений и применяется в решении двумерных уравнений методом продольно-поперечных прогонок (пусть его решение представляется двумерные массивом, а разностные коэффициенты тоже как-то хранятся), то операции выборки сеточных функция и передачи параметров процедуры понизят на порядок эффективность всего алгоритма.
- Обработка и анализ результатов. Непосредственным результатом решения сеточных уравнений являются числовые массивы, которые для многомерных задач дают необозримое море информации. Пользователю, как правило, требуются значения решения в отдельных точках и на некоторых линиях или же обработанные данные величины экстремальных значений и координаты соответствующих им точек, изолинии, векторные поля градиентов, различные функционалы от решения. Немаловажную роль играет наглядность результатов, для чего используются рисунки, таблицы, различные форматы чисел, заголовки и текстовые пояснения, что намного повышает удобство эксплуатации пакетов, вывод промежуточных данных, сообщение о ходе выполнения этапов вычислительного процесса, диагностику допущенных ошибок пользователя с рекомендациями по их устранению, оценку погрешности расчетов (если их можно получить). Для всех этих целей разрабатываются специальные алгоритмы и программные модули или используются средства базового программного обеспечения, в том числе машинной графики. Средства вывода должны обеспечить оперативность и полноту анализа. На основе полученных данных могут быть приняты решения об изменении математической постановки задачи, численных методов или модификации программы, если пользователя не устраивает точность или экономичность расчетов и если он имеет квалификацию на уровне разработчика пакета.
Литература:
- Ильин В. П. Численные методы решения задач электрооптики // Новосибирск: Наука. 1974.
- Мещеряков Ю. П., Шапеев В. П Некоторые неометрические методы построения разностных сеток в областях с криволинейными границами. –Численные методы механики сплошной среды, Новосибирск, 1978, т. 9, № 2, с. 91–103.
- Олимов М., Каримов П., Исмоилов Ш. К решению краевых задач пространственных стержней при переменных упруго-пластических нагружений с учетом разгрузки // Научно- технический журнал ФерПИ, Фергана — 2014. — № 3 — с. 113–116.
- Олимов М., Каримов П., Исманова К., Исмоилов Ш «Математической пакет прикладной программа» // Учебник пособия // Тошкент-2015 г// Издат:.«Тафаккур».







