В данной работе рассматривается симметричная трехдиагональная матрица размера 3х3. Используя формулы Кардано для решения кубического уравнения, находим формулу для числового образа.
Пусть Н гильбертово пространство и 
линейный оператор с областью определения 
. Тогда множество 
называется числовым образом оператора 
[1–3].
Пусть 
множество комплексных чисел. В пространстве 
рассмотрим матрицу вида:
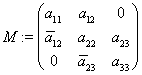
размера 
, где 
произвольные вещественные числа, а 
произвольные комплексные числа.
Положим:
;
;
.
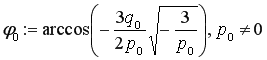Теорема 1. Если
то 
, то
.
Доказательство. Найдем собственные числа матрицы 
. Для этого мы должны знать решение уравнения:
(1)
где 
. Приведем некоторые сведение о решение этих уравнений. Положим:
.
Возможны три случая:
-
Если
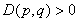, то уравнение (1) имеет одно вещественное и два взаимно сопряженных комплексных решения.
-
Если
, то уравнение (1) имеет три вещественных решения и по крайней мере два из них равны:
при 
, числа 
;
при 
, числа 
;
при 
, числа 
является решениями уравнения (1). Здесь 
, т. е. из 
следует, что 
.
-
Если
,то уравнение (1) имеет три разных решений следующего вида:
где
.
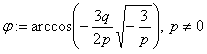Используя свойства косинуса имеем 
. Заметим, что:
если , то уравнение (1) имеет два положительные и одно отрицательное решение;
если 
, то уравнение (1) имеет одно положительное и две отрицательные решения;
если 
, то все решения уравнении (1) являются вещественными тогда и только тогда когда 
.
Собственные числа матрицы 
являются нулями характеристического уравнения
(2)
Найдем решение уравнения (2).
Делая замену переменных 
уравнение (2) перепишем в виде:
.
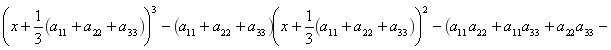
После простых вычислений имеем:
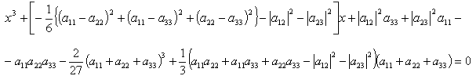(3)
Обозначая
;
получим, что уравнение (3) имеет вид 
.
Решение этого уравнения имеет вид:
.
Здесь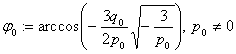 
.
В этом случае решение уравнения (2) имеет вид:
.
Причем для 
имеет место соотношение 
.
Следовательно, имеет место равенство 
, где
.
Теорема доказана.
Литература:
- Hausdorff F. Der Wertvorrat einer Bilinearform // Math. Z., 3:1 (1919), pp. 314–316.
- Heydari M. T. Numerical range and compact convex sets // Rend. Circ. Mat. Palermo, 60 (2011), pp. 139–143.
- Langer H., Markus A. S., Matsaev V. I., Tretter C. A new concept for block operator matrices: the quadratic numerical range // Linear Algebra Appl., 330:1–3 (2001), pp. 89–112.
