Дифференциальное уравнение движения бипланетарного механизма
Рассмотрим бипланетарный механизм (рисунок). Угловые скоростиводила H сателлита 1, водила h сателлита 4, колес 3 и 4 обозначим φH, φh, φ3и φ4.
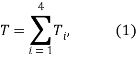
где
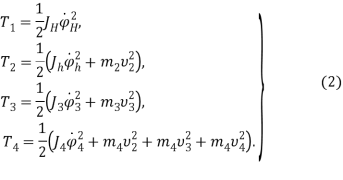
Подставив выражения (2). в (1), получим
![]()
![]()
здесь
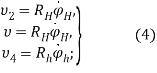
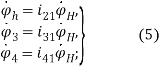
Подставив значения из (4) и (5). в (3), найдем
![]()
![]()
или
![]()
Введем обозначение
![]()
тогда значение T будетравно
![]()
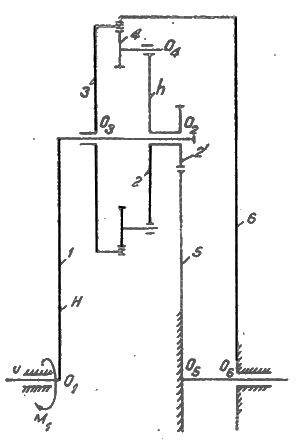
Кинематическая схема бипланетарного механизма: 1-водило H; 2-водило h; 3,4- сателлиты; 5,6- неподвижные центральные колеса.
Для определения дифференциального уравнения движения бипланетарного механизма воспользуемся уравнением Лагранжа второго рода.
![]()
Теперь найдем производные, входящие в уравнение (7):
![]()
откуда
![]()
Для определения обобщенной силы ![]() вычислим элементарную работу активных сил и моментов.
вычислим элементарную работу активных сил и моментов.
Механизм расположен в горизонтальной плоскости и, значит, работа сил тяжести его звеньев равна нулю. Поэтому элементарная работа имеет вид:
![]()
где
Подставив (11) в (10), запишем
![]()
или
![]()
Выражение в скобках есть обобщенная сила ![]()
![]()
где
![]()
Используя значения (13) в (12), получим выражение
![]()
Введем обозначение
![]()
и, подставив значения обобщенной силы в (9), найдем
![]()
Это уравнение является дифференциальным уравнением бипланетарного механизма, только без технологических сопротивлений.







