Рассмотрим кубатурную формулу общего вида
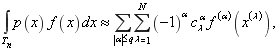 (1)
(1)
над пространством С. Л. Соболева ![]() . Здесь, соответственно,
. Здесь, соответственно,![]() и
и ![]() являются коэффициентами и узлами кубатурной формулы (1),
являются коэффициентами и узлами кубатурной формулы (1), ![]() — весовая функция,
— весовая функция, ![]() ,
, ![]() —
— ![]() -мерный тор и
-мерный тор и ![]() — порядок обобщенных производных и
— порядок обобщенных производных и ![]() .
.
Определение 1. Множество ![]() , где
, где ![]() , т. е. дробная доля
, т. е. дробная доля ![]() , называется
, называется ![]() -мерным тором
-мерным тором![]() .
.
Определение 2. Пространство ![]() — определяется как пространство функций, заданных на
— определяется как пространство функций, заданных на ![]() - мерном торе
- мерном торе ![]() и имеющих все обобщенные производные порядка
и имеющих все обобщенные производные порядка ![]() суммируемые с квадратом в норме [1–4]
суммируемые с квадратом в норме [1–4]
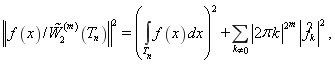 (2)
(2)
со скалярным произведением
![]()
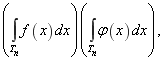 (3)
(3)
где ![]() — коэффициенты Фурье, т. е.
— коэффициенты Фурье, т. е. ![]() .
.
Разность между интегралом и кубатурной суммой, т. е.
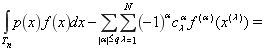
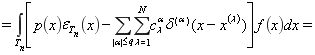
![]()
называется погрешностью кубатурной формулы (1), и этой разности соответствует обобщенная функция
![]() (4)
(4)
и назовем ее функционалом погрешности кубатурной формулы (1). Здесь ![]() — характеристическая функция
— характеристическая функция ![]() .
.
Задача построения оптимальных кубатурных формул над пространством Соболева ![]() — это вычисление следующей величины:
— это вычисление следующей величины:
![]() (5)
(5)
где ![]() — сопряженное пространство к пространству
— сопряженное пространство к пространству ![]() . Для оценки погрешности кубатурной формулы необходимо решить следующую задачу.
. Для оценки погрешности кубатурной формулы необходимо решить следующую задачу.
Задача 1. Найти норму функционала погрешности (4) данной кубатурной формулы.
Сначала мы должны вычислить норму ![]() функционала погрешности
функционала погрешности ![]() в пространстве
в пространстве ![]() , а потом если требуется построить оптималную кубатурную формулу, варьируя
, а потом если требуется построить оптималную кубатурную формулу, варьируя ![]() и
и ![]()
![]() , необходимо решить следующую задачу
, необходимо решить следующую задачу
Задача 2.Найти такие значения ![]() и
и ![]() , чтобы выполнялось равенство (5).
, чтобы выполнялось равенство (5).
В настоящей работе занимаемся решением задачи 1 для кубатурной формулы общего вида (1), т. е. вычислением нормы
Теорема 1.Квадрат нормы функционала погрешности (4) кубатурной формулы общего вида (1) над пространством ![]() равен
равен
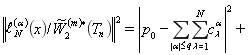
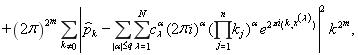 (6)
(6)
где ![]() — коэффициенты,
— коэффициенты, ![]() — узлы кубатурной формулы (1) и
— узлы кубатурной формулы (1) и ![]() — коэффициенты Фурье функции
— коэффициенты Фурье функции ![]() , т. е.
, т. е. ![]() .
.
Справедлива следующая
Теорема 2.Функция ![]()
является экстремальной функцией для кубатурной формулы (1) и ![]() .
.
На основании теоремы 1 функционал погрешности (4) кубатурной формулы (1) для функций из класса ![]() имеет оценку: [4]
имеет оценку: [4]
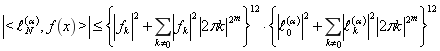
Литература:
- Соболев С. Л. Введение в теорию кубатурных формул. М.: Наука, 1974. — 808с.
- Рамазанов М. Д. Лекции по теории приближенного интегрирования. Уфа, 1973. — 173с.
- Салихов Г. Н. Кубатурные формулы для многомерных сфер. Ташкент: Фан, 1985. — 104 с.
- Шарипов Т. Х. Некоторые вопросы теории приближенного интегрирования. Диссертация кандидата физ.-мат. наук. Ташкент, 1975. — 102 с.







