К оценке погрешности весовых кубатурных формул в пространстве

Постановка проблемы оптимизации формул приближенного интегрирования в современном понимании выглядит как проблема отыскания минимума нормы функционала погрешности , заданного на некотором пространстве функций. Поэтому вычисление нормы функционала погрешности кубатурных формул на этих пространствах функций играют важную роль для построения оптимальных кубатурных формул [1–3].

Многомерные кубатурные формулы отличаются от одномерных двумя особенностями:

1) бесконечно разнообразны формы многомерных областей интегрирования;

2) быстро растёт число узлов интегрирования с увеличением размерности пространства.

Проблема 2) требует особого внимания для построения наиболее экономичных формул.

Существуют различные принципы построения кубатурных формул. Классический принцип, который относится к работе [1–3] и теоретико — функциональный принцип в теории приближенного интегрирования.

Настоящая работа ведется теоретико — функциональным подходом, поэтому ниже опишем необходимые сведения из этого подхода. Рассмотрим кубатурную формулу вида

где — некоторая область в Евклидовом пространстве , — коэффициенты (веса), а — узлы кубатурной формулы (1). Погрешностью кубатурной формулы (1) называется разность

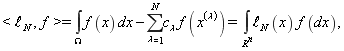(2)

(3)

, — дельта функция Дирака, — число узлов. В (2) и (3) — называется функционалом погрешности кубатурной формулы (1).

Пусть функция принадлежит некоторому пространству Банаха , тогда будет функционалом из сопряженного пространства . Предполагается, что это пространство компактно вложено в пространство непрерывных функций, заданных в области :

Функционал заданный на линейный и непрерывный, а в силу условия (4) и ограниченный, т. е. имеем:

Из оценки (5) видно, что качество кубатурной формулы характеризуется нормой функционала погрешности, которая определяется формулой

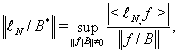
и является функцией неизвестных коэффициентов и узлов. Поэтому для вычислительной практики полезно уметь вычислить норму функционала погрешности (6) и оценить ее. Отыскание минимума нормы функционала погрешности по и есть задача на исследование функции многих переменных на экстремум. Значения и , реализующие этот минимум, определяют оптимальную формулу. Таким образом, оптимальной кубатурной формулой мы будем считать такую, в которой при заданном числе узлов функционал погрешности имеет наименьшую норму.

Настоящая работа посвящена для функций n — переменных

, где — n мерных тор.

Определение 1. Множество , где , т.е дробная доля , называется n — мерным тором .

Определение 2. Пространство определяется как замыкание множества конечных рядов Фурье

в полунорме 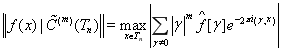, (7)

где и

т. е. коэффициенты Фурье.

Рассмотрим кубатурную формулу.

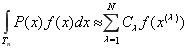,(8)

где — весовая функция, — коэффициенты и — узлы кубатурной формулы (8).

Кубатурной формулы (8) сопоставим обобщенную функцию

и назовем ее функционалом погрешности.

Здесь — функция Дирака и — характеристическая функция тора , т. е.

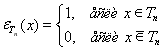
Задача построения наилучших кубатурных формул над пространством — это вычисление следующей величины:

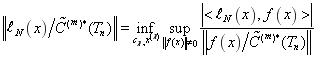, (10)

где — сопряжённое пространство к пространству .

Для оценки погрешности квадратурной формулы необходимо решить следующую задачу.

Задача 1. Найти норму функционала погрешности (9) данной кубатурной формулы (8). Сначала мы должны вычислить норму функционала погрешности в пространстве , а потом если требуется построить наилучшую кубатурную формулу, варьируя и , необходимо решить следующую задачу.

Задача 2. Найти такие значения и , чтобы выполнялось равенство (10).

В настоящей работе займёмся решением первой задачи для весовой кубатурной формулы (8), т. е. вычислением нормы функционала погрешности кубатурной формулы (8).

Теорема. Для нормы функционала погрешности (9) кубатурной формулы (8) в пространстве имеет место следующего равенства

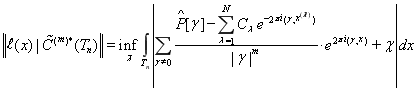, (11)

где - произвольное действительное число.

Литература:

1. Соболев С. Л., Введение в теорию кубатурных формул. М.: Наука, 1974. — 808с.
2. Салихов Г. Н., Кубатурные формулы для многомерных сфер. Ташкент: Фан, 1985–104 с.
3. Шарипов Т. Х. Некоторые вопросы теории приближенного интегрирования кандидатская диссертация. Ташкент 1975–102с.