Механика упругой среды или теории упругости занимается деформацией и движением упругих тел под влиянием внешних воздействий, в качестве которых рассматриваются поверхностные нагрузки, массовые силы (например, вес), нагревание или охлаждение тела. Отсюда основной задачей механики упругой среды является определение перемещений любой точки тела по заданной внешней нагрузке. Для постановки и решения подобных задач первоначально необходимо провести математическое моделирование механики упругой среды [1].
Пусть в упругом полупространстве 
со свободной от напряжений границей имеется включение в виде полосы: 
,
, расположенное в плоскости 
.
Требуется найти поле напряжений и смещений, если к внешнему краю указанного включения приложена равномерно распределенная сдвигающая нагрузка интенсивности 
Сформулированная задача эквивалентна следующей краевой задаче
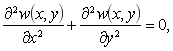
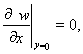(1)
в которой уравнение Лапласа должно удовлетворяться всюду, кроме 
(области, занятой включением).
При переходе через включение касательное напряжение 
терпит разрыв, а смещения непрерывны и постоянны, то есть
(2)
Роль интегрального преобразования будет выполнять преобразование Фурье [2]. Умножим (1) на 
, проинтегрируем по частям раздельно на интервалах 
, 
и на основании (2) получаем следующую одномерную краевую задачу:
(3)
Фундаментальная функция уравнения (3) имеет вид (5), через которую решение задачи (3) запишется в виде
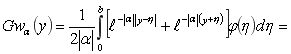
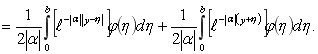
Во втором интеграле введем замену 
и доопределим функцию 
, получаем
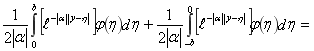
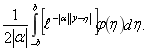
Следовательно,
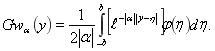(4)
Обращая полученную трансформанту, находим,
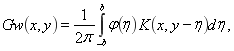
где
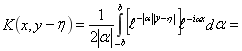
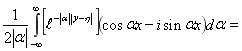
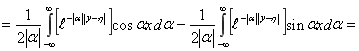
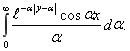
Окончательно, для жесткого включения
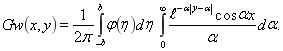(5)
Как видим из (5), смещения выражаются через расходящийся интеграл. Чтобы от него избавиться, следует перейти к относительным смещениям, то есть
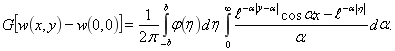
Получим сходящийся интеграл для относительных смещений, вычислим его
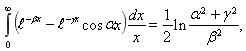
Тогда
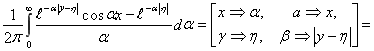
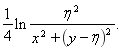(6)
Получаем следующую формулу для смещений
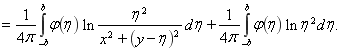
Откуда
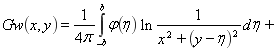
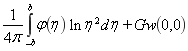
или
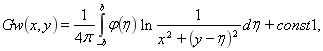(7)
где
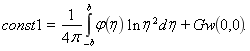
Реализуем второе условие из (2), приходим к
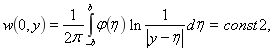
(8)
Уравнение (8) решаем с помощью спектрального соотношения
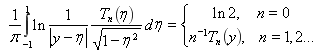(9)
Для применения (9) к (8) сделаем замену
,
то есть перейдем к интервалу (-1,1). Решение ищем в виде
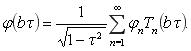(10)
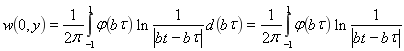
В результате получаем
или 
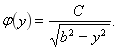(11)
Произвольную постоянную реализуем с помощью условия включения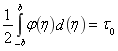 
или
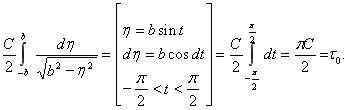
Окончательно 
запишется в виде
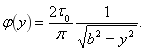(12)
Подставляя (12) в (7), получаем формулу для смещений
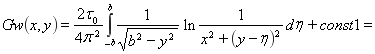
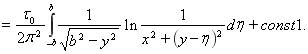(13)
Так как касательные напряжения 
и 
, тогда с учетом (13) получим
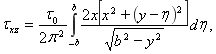
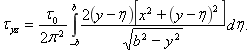
Последние три формулы и определяют решение поставленной антиплоской задачи для полупространства с жестким включением. Построенное решение может быть использовано при рассмотрении соответствующих технических проблем, когда их модель сводится к решению указанной задачи.
Литература:
- Попов Г. Я., Абдыманапов С. А., Ефимов В. В., Игликов А. И. Метод разрывных решений в задачах математической физики. — Караганда, 1993. — с.97.
- Работнов Ю. Н. Механика деформируемого твердого тела. М.: Наука, 1997. — с.744.
