Обработка данных геомониторинга на основе сингулярного спектрального анализа



Одним из мощных методов анализа временных рядов является метод «Гусеница» (называемый в зарубежной литературе SSA – Singular Spectrum Analysis). Наиболее исследованным является одномерный метод SSA [1, 2], предназначенный для анализа одного вещественнозначного временного ряда.

Для одномерного ряда базовый метод SSA состоит в преобразовании исходного ряда в многомерный, сингулярном разложении получившейся траекторной матрицы, группировке членов разложения и последующем восстановлении.

При этом часто оказывается возможным выделить отдельные аддитивные составляющие исходного ряда, такие как тренд (гладкая и медленно меняющаяся часть ряда), различные колебательные и периодические компоненты, а также шумовую компоненту.

Способ преобразования одномерного ряда в многомерный представляет собой свертку временного ряда в матрицу, содержащую фрагменты временного ряда, полученную с некоторым сдвигом. Общий вид сдвиговой процедуры напоминает гусеницу, поэтому сам метод нередко так и называют – «Гусеница».

Базовый алгоритм метода «Гусеница» SSA

Пусть . Рассмотрим вещественный временной ряд длины . Будем предполагать, что ряд F – не нулевой, т.е. существует, по крайне мере, одно i такое, что . Числа могут быть интерпретированы не только как дискретный момент времени, но и как некоторые метки, имеющие линейно-упорядоченную структуру.

Первый этап: разложение

Вложение.Процедура вложения переводит исходный временной ряд в последовательность многомерных векторов. Пусть L некоторое целое число (длина окна), . Процедура вложения образует векторов вложения ; , имеющих размерность . – траекторная матрица ряда F состоит из векторов вложения в качестве столбцов: .

Другими словами, траекторная матрица – это матрица

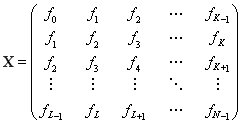.(1)

Очевидно, что и матрица X имеют одинаковые элементы на побочных диагоналях. Такая матрица называется ганкелева.

Сингулярное разложение. Результатом этого шага является сингулярное разложение (SVD–SingularValueDecomposition) траекторной матрицы ряда. Пусть . Обозначим собственные числа матрицы , взятые в неубывающем порядке и – ортонормированную систему собственных векторов матрицы , соответствующих собственным числам.

Пусть Если обозначить то сингулярное разложение матрицы Х может быть записано как

(2)

где Каждая из матриц имеет ранг 1. Поэтому их можно назвать элементарными матрицами.

Набор () мы будем называть i-ой собственной тройкой сингулярного разложения (2).

Второй этап: восстановление

Группировка.На основе разложения (2) процедура группировки делит все множество индексов {1,…,d} на mнепересекающихся подмножеств . Пусть Тогда результирующая матрица , соответствующая группе I, определяется как . Такие матрицы вычисляются для , тем самым разложение (2) может быть записано в сгруппированном виде

(3)

Процедура выбора множеств называется группировкой собственных троек.

Диагональное усреднение. На последнем шаге алгоритма каждая матрица сгруппированного разложения (3) переводится в новый ряд длины N. Пусть Y – некоторая LхK матрица с элементами , где Положим и Пусть если и иначе. Диагональное усреднение переводит матрицу Yв ряд по формуле (4).

Выражение (4) соответствует усреднению элементов матрицы вдоль «диагоналей» : выбор дает для получаем и т.д. Заметим, что если матрица Yявляется траекторной матрицей некоторого ряда (другими словами, если матрица Y является ганкелевой), для всех i.

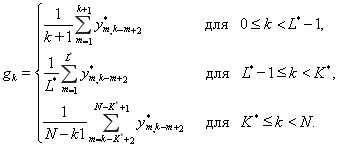
Применяя диагональное усреднение (4) к результирующим матрицам , мы получаем ряды и, следовательно, исходный ряд раскладывается в сумму mрядов:

(5)

Сингулярное разложение

Сингулярное разложение является основой математической части метода. Большинство его свойств справедливо для произвольной матрицы , но ганкелева структура траекторной матрицы добавляет ряд особых свойств. Определим сингулярное разложение произвольной ненулевой -матрицы как разложение X в виде

(6)

где – собственные числа матрицы упорядоченные по убыванию, – соответствующая система ортонормированных собственных векторов матрицы S и

В стандартной терминологии называются сингулярными числами; и – левыми и правыми сингулярными векторами матрицы Х соответственно. Набор называется i-ой собственной тройкой матрицы Х. Заметим, что строки и столбцы траекторной матрицы являются отрезками исходного ряда. Поэтому левый и правый сингулярные векторы так же имеют временную структуру и могут рассматриваться как временные ряды.

Если определить то представление (6) может быть переписано в виде (2), т.е. как представление X в виде суммы элементарных матриц. При этом собственное число является характеристикой вклада матрицы в разложение. Так как сингулярное разложение имеет дело с матрицей Xкак единым целым, оно не инвариантно относительно перестановки ее столбцов

Более того равенство (6) показывает, что сингулярное разложение обладает свойством симметричности: образуют ортонормированную систему собственных векторов матрицы ,соответствующих тем же самым собственным числам .

Пример работы программы «Гусеница»

Одним из вычислительных инструментов анализа воздействий внешних факторов является программа solid.exe. Используя данную программу, может быть получен расчет трехмерных координат смещения точки на твердой поверхности земли. Несмотря на то, что программа solid.exe способна предоставить информацию до июня 2015 г., осенью появилась новая модифицированная версия. На смену пришел специализированный пакет Solidearthtide, написанный JoseGama под язык программирования и систему статистических вычислений R. Для того чтобы получить координаты смещения точки, необходимо сначала подключить пакет (рис.1), а затем написать команду CalculateTide[название, год, месяц, день, широта, долгота, булева переменная (TRUE = представить данные в виде матрицы)]. В результате выполнения программы, на экране представлены координаты смещения точки с минутным интервалом (рис. 2).

Метод «Гусеница»-SSA независимо разрабатывался и в России и в Великобритании под различными названиями: «Гусеница» и SSA (SingularSprectrumAnalysis). Он применяется для анализа временных рядов и может решать различные задачи, такие как, выделение тренда, обнаружение периодик, сглаживание ряда, построение полного разложения ряда в сумму тренда, периодик и шума.

Рис. 1. Подключение пакета в языке R

Рис. 2. Пример работы программы

Трехмерные данные, полученные с помощью пакета Solidearthtide, можно графически представить с помощью программы «Гусеница», где по оси Х – время, по У – смещение; верхняя кривая – это направление Восток-Запад, средняя – Север-Юг, а нижняя – Вверх-Вниз (рис. 3). В результате применения программы «Гусеница» получаем исходный и восстановленный ряды (в нашем случае они совпали), а также ряд остатков, играющий принципиальную роль при анализе временного ряда (рис. 4).

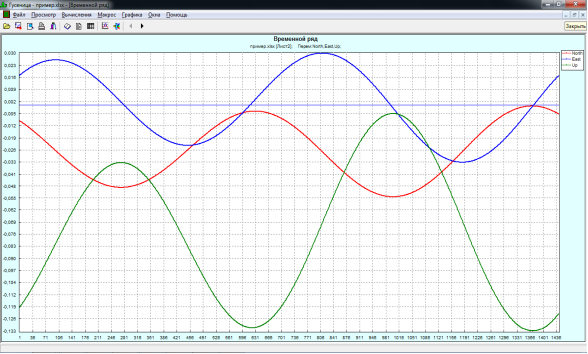
Рис. 3. Графическое представление трехмерного временного ряда

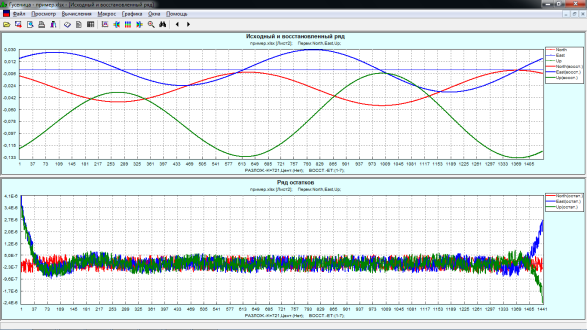
Рис. 4. Результат работы программы «Гусеница»

Актуальность выделения предвестников землетрясений очевидна, так как до сих пор ни один предложенный метод не может с высокой точностью определить время, место и силу землетрясений.

Литература:

1. Голяндина Н.Э. Метод «Гусеница»-SSA анализа временных рядов: учебное пособие. – СПб: 2004. – 76 с.
2. Данилов Д.Л. Главные компоненты временных рядов: метод «Гусеница» / А.А. Жиглявский. – СПб: СПбГУ, 1997. – 308 с.
3. Официальный сайт CaterpillarSSA [Электронный ресурс] сайт для скачивания утилиты CaterpillarSSA // http://www.gistatgroup.com/gus/index.html
4. Мельхиор П. Земные приливы. – М.: Мир, 1968. – 482 с.
5. Уильямс Дж.Е. Приливные ритмы: ключ к истории вращения Земли и эволюции лунной орбиты // J. Phys. Earth. – 1990.
6. Dennis Milbert SOLID EARTH TIDE. Электронный ресурс. – Режим доступа: http://home.comcast.net/~dmilbert/softs/solid.htm (дата обращения 10.12.2014).
7. Салтыков В.А. Механизм приливных эффектов в сейсмичности на основе модели амплитудно-зависимой диссипации // Физическая мезомеханика. – 2014. – Вып. № 5. – Т. 17. – С. 103–110.
8. Sachiko Tanaka, Masakazu Ohtake, and Haruo Sato. Evidence for tidal triggering of earthquakes as revealed from statistical analysis of global data // J.GEOPHYSICAL RESEARCH. – 2002. – Vol. 107, No. B10. – Р.2211.
9. Laurent Métivier, Olivier de Viron, Clinton P. Conrad, Stéphane Renault, Michel Diament, Geneviève Patau. Evidence of earthquake triggering by the solid earth tides // Earth and Planetary Science Letters. – 2009. – Vol. 278. – P. 370–375.
10. XIE Chao-Di, WU Xiao-Ping, LEI Xing-Lin, MAO Wei, SUN Nan. Long-period tides and global earthquake energy release // Chinese Journal of Geophysics. – 2013. – Vol. 56, No. 6. – P. 823–832.
11. Sibgatulin V.G., Peretokin S.A., Kabanov A.A. Resonances of gravitational tides and their effect on geological environment // Earth science frontiers. – 2014. – Vol. 21 (4). – P. 303–310.