О строении одной разрешимой алгебры Лейбница

 

In this paper we consider Leybniz algebra with a known nilradical. It proved that such an algebra is decomposed as a direct sum of its nilradical and two-dimensional complementary subspace.

 

Определение 1. Алгебра G над полем F называется алгеброй Ли, если для любых x,y,zG выполняется тождества:

[x,x]=0 — антикоммутативности,

[[x,y],z]+ [[y,z],x]+ [[z,x],y]=0 — Якоби,

где [,] — умножение в G.

Определение 2. Алгебра L над полем F называется алгеброй Лейбница, если для любых x,y,zL выполняется тождество Лейбница:

[x, [y,z]]= [[x,y],z]- [[x,z],y]

где [,] — умножение в L.

Заметим, что если в L выполняется тождество [x,x]=0, то тождество Лейбница преобразуется в тождество Якоби. Таким образом алгебры Лейбница являются ’’некоммутативным’’ аналогом алгебр Ли.

Подалгебру H алгебры ЛейбницаL назовем двусторонним идеалом если [L,H]L и [H,L] L.

Для произвольной алгебры Лейбница L с помощью соответственных двусторонних идеалов рекурсивным образом определяются нижний, центральный и производные ряды соответственно последовательностями

L¹=L, Lⁿ⁺¹= [Lⁿ,L¹], и L ^[1]=L, L ^[n+1]= [L ^[n],L ^[n]], .

Определение 3. Алгебра Лейбница L называется разрешимой, если существует mN такое, что L ^[m]=0. Натуральное число m называется индексом разрешимости алгебры L, если L ^[m-1]0 и L ^[m]=0.

Алгебра Лейбница L называется нильпотентной, если существует sN такое, что L^s=0. Минимальное число s, обладающее таким свойством называется индексом нильпотентности (нильиндексом) алгебры L, т. е. L^s-10 и L^s=0.

Замечание. Нетрудно видеть, что индекс нильпотентности произвольной n-мерной нильпотентной алгебры не превосходит числа n+1.

Определение 4. Максимальный нильпотентный идеал алгебры Лейбница называется нильрадикалом этой алгебры.

Определение 5. Линейное преобразование d алгебры Лейбница L называется дифференцированием, если

d([x,y])= [d(x),y]+ [x,d(y)]

для любых x, yL.

Определение 6. [8]. Пусть дифференцирования алгебры Лейбница L. Дифференцирования называются ниль-независимыми если

не является нильпотентной для всех скаляров .

Другими словами, если для всех скаляров , существует натуральное число такое, что если , то .

Пустьразрешимая алгебра Лейбница. Тогда она может быт представлена в виде разложения , где есть нильрадикал, а  — векторное пространство-дополнение [5].

Теорема 1. Пусть алгебра Лейбница и её нильрадикал. Тогда размерность векторного пространства-дополнения к не больше чем максимального количества ниль-независимых дифференцирований . [5]

Изучения алгебр Лейбница со структурной точки зрения является одной из актуальных задач теории алгебр Ли и алгебр Лейбница.

В статье [4] приводится и изучается некоторые свойства алгебр со следующими структурными строениями

M: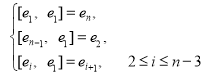

В настоящей статье изучаем строение алгебр Лейбница имеющие такие алгебры в качестве нильрадикала.

В следующем предложении описаны пространства дифференцирований алгебр Лейбница M.

Теорема 2. Всякое дифференцирование алгебры Лейбница M имеет следующий вид:

 

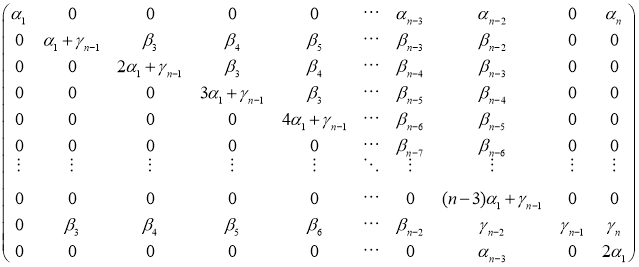
Доказательство. Зададим дифференцирование в алгебре M в виде:

, ,

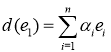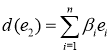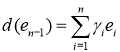
Рассмотрим свойство дифференцирования:

1)

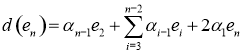
2)

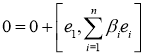, отсюда , следовательно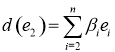

3)

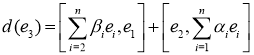
Отсюда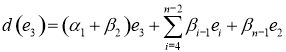

4)

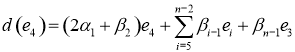
5)

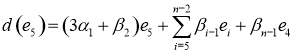
По математической индукции нетрудно доказать, что имеет место

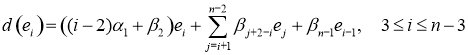(1)

Тогда

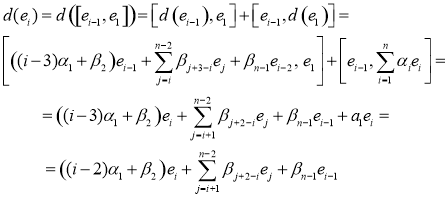
6) . Отсюда имеем

7) Отсюда , следовательно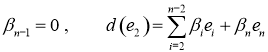

8)

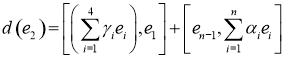
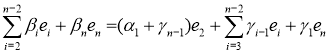отсюда следует

. Следовательно

,

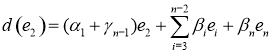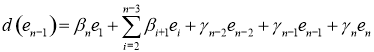
9) ,

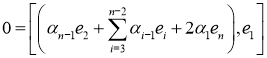
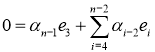отсюда

Следовательно

10)

.

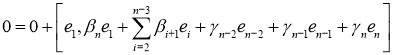
Итак, ,

, ,

, ,

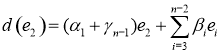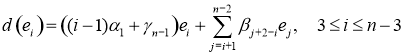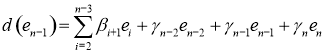Теорема доказана.

Отсюда нетрудно видеть, что число нильнезависимых дифференцирований равно двум и с учетом теоремы 1 приходим к выводу, что имеет место

Теорема 3. Любая разрешимая алгебра Лейбница имеющая алгебру M качестве нильрадикала может быт представлена в виде разложения , где  — векторное пространство-дополнение к M имеющая размерность равная двум.

 

Литература:

 

1. Аюпов Ш. А., Омиров Б. А. О некоторых классах нилъпотентных алгебр Лейбница // Сиб. матем. ж. 2001. Т. 42. № 1. С. 18–29.
2. S. A. Ayupov, B. A. Omirov, On Leibniz algebras, in: Algebra and operator theory (Tashkent, 1997), Kluwer Acad. Publ., Dordrecht, 1998, pp. 1–12.
3. D. W. Barnes, On Levi’s theorem for Leibniz algebras, arXiv:1109.1060v1.
4. L. M. Camacho, E. M. Canete, J. R. Gomez, B. A. Omirov, Quasi-filiform Leibniz Algebras of maximum length. arXiv:1009.2148v1.
5. J. M. Casas, M. Ladra, B. A. Omirov, I. A. Karimjanov, Classification of solvable Leibniz Algebras with null-filiform Nilradical. Linear and Multilinear Algebra, 2013 vol.61, N6 p 758–774.
6. J.-L. Loday, une version non commutative des algebras de Lie: les algebras de Leibniz, Enseign. Math.(2) 39 (3–4) (1993) 269 -293.
7. A. I. Malcev, Solvable Lie algebras, Amer. Math. Soc. Translation 1950 (27) (1950).
8. G. M. Mubarakzjanov, On solvable Lie algebras, Izv. Vysš. Učehn. Zaved. Matematika 1963 (no 1 (32)) (1963) 114–123.