В статье рассматриваются учебные компьютерные программы как один из распространенных видов учебных моделей. В качестве примера приводятся программы, моделирующие движение маятников.
Ключевые слова: вычислительный эксперимент, компьютерное моделирование, маятник, математический маятник, модель, пружинный маятник, учебная компьютерная модель, физический маятник.
Представленность в нашем сознании природных явлений детерминирована тремя видами этих явлений (М. К. Мамардашвили):
— явления бытия, или физические явления, в самом широком смысле этого слова (по определению М. К. Мамардашвили «явления первого рода»);
— суждения о физических явлениях, возникающие в результате активного созерцания, имеющего деятельностную (А. Н. Леонтьев) природу («явления второго рода);
— явления смешанного характера, ставшие когда-то предметом исследования З. Фрейда («явления третьего рода»).
Опосредованная представленность явлений как первого рода, так и второго рода в форме модели подразумевает собой:
— процесс создания модели (моделирование);
— наличие внешнего по отношению к сознанию субъекта средства создания модели (инструмента моделирования).
В настоящее время компьютерные программы являются одним из распространенных видов моделей [1, с. 5–6; 2; 3]. В них реализованы (т. е. учтены и воспроизведены в какой-либо форме) наиболее существенные признаки явлений и процессов. Чаще всего с помощью таких моделей изучаются элементы каких-либо сложных систем и отношения между ними. Анализ многих современных программных продуктов, моделирующих явления и процессы, говорит о том, что доминирующим объектом моделирования для разработчиков компьютерных программ являются по-прежнему явления первого рода, в то же время неразрывно связанные с ними явления второго рода нередко остаются вне поля зрения тех, кто занимается моделированием. Попробуем указать подходы к конструированию моделей второго рода. Для этого обратимся к теории, учитывающей структуру деятельности, принципы функционирования и закономерности развития. Из общих положений теории деятельности следует, что в модели необходимо отразить операции, действия и рефлексивные компоненты как весьма существенные структурные элементы деятельности. Задача по определению характеристик компьютерной программы, предназначенной для построения такой модели, состоит в создании композиции, то есть в выборе объектов для отображения на экране компьютера. В этом случае удобно воспользоваться методом, также хорошо известном из теории деятельности. Даже если мы ограничимся только операциональной составляющей деятельности, это может позволить получить вполне приемлемые результаты конструирования модели. История возникновения графических образов отображения реальности позволяет сделать предположение о том, что изменение этих образов шло по пути абстрагирования и происходило в три этапа. Первый этап являлся предметным, он соответствовал представлениям, которые являлись трехмерными объектами. Второй этап (знаково-символический) соответствовал плоским (двумерным) объектам. Третий этап был только знаковым (текстуальным). При решении задачи создания компьютерной модели представление объектов в трехмерном пространстве ввиду технических ограничений экрана обычного компьютера в современных условиях может быть реализовано только в псевдотрехмерной форме. Тем не менее, это является возможным. В качестве объектов предельной абстракции в данном случае могут выступать простейшие геометрические тела, к которым относятся куб, шар, цилиндр и конус. Эти тела при определенных условиях могут быть трансформированы в плоские геометрические фигуры: куб — в квадрат, шар — в круг, цилиндр — в прямоугольник, конус — в треугольник. И наконец, последней формой представленности действительности является текст, который определенным образом описывает модель. Учитывая последовательность таких трансформаций можно моделировать структурные компоненты обучающих человеко-машинных систем, с помощью которых будет осуществляться переход от абстрактного к конкретному представлению в обучении.
Связь понятий «моделирование» и «отражение» предполагает такую организацию интерфейса компьютерной программы, в которой была бы предусмотрена функция ориентирования обучающегося в самой модели для получения им информации в нужном обучающему контексте. Например, модель может иметь историю (или изменяться). Она может усложняться или упрощаться, при этом обучающийся должен понимать наблюдаемое текущее состояние модели как результат ее эволюции. Следует также учесть особенности целостного восприятия объектов согласно принципам гештальт-психологии. В созданных нами обучающих программах мы старались учесть все представленные выше требования.
Основополагающими характеристиками при создании модели должны быть:
— обусловленная абстрактность графических объектов и отношений между ними;
— генезис графических средств отображения информации;
— упорядоченные по степени обобщенности операции и действия;
— включенность оценочных и рефлексивных действий;
— дифференцированность этапов конструирования модели и использования модели;
— одномоментность топологических, динамических и энергетических форм модели.
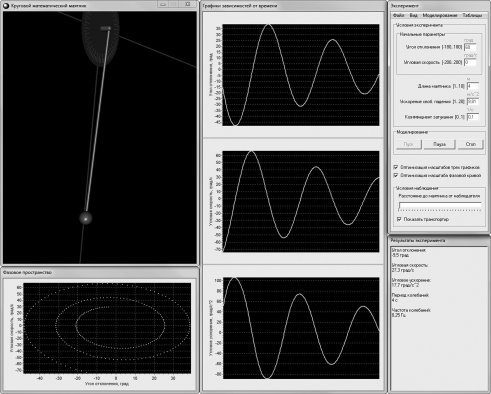
Рис. 1. Учебная компьютерная модель математического маятника
Для изучения механических колебаний мы разработали и создали учебные компьютерные модели следующих идеальных колебательных систем:
— кругового математического маятника (рис. 1);
— двойного кругового математического маятника (рис. 2);
— математического маятника с бифилярным подвесом (рис. 3);
— вертикального пружинного маятника (рис. 4);
— вертикального двойного пружинного маятника (рис. 5);
— двух круговых математических маятников, связанных пружиной (рис. 6);
— физического маятника (рис. 7).
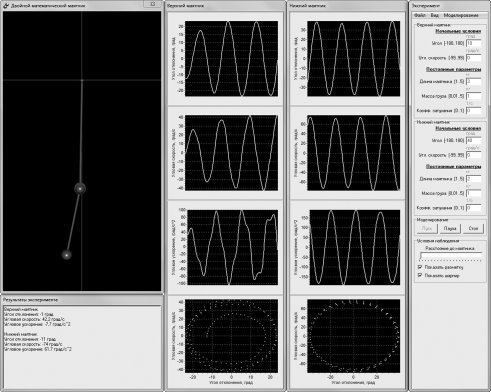
Рис. 2. Учебная компьютерная модель двойного математического маятника
Рассмотрим, что представляют собой эти модели, и как они соответствуют заявленным выше требованиям. Все модели реализованы в виде многооконных приложений для операционных систем семейства Windows. Они имеют окно, в котором представлена образная (наглядная) модель, которую будут исследовать обучающиеся. Формируя ее изображение, мы не стремились к излишней правдоподобности образа, как это делают во многих подобных приложениях, делая акцент на том, что это не реальный объект, а идеальный (абстрактный). Возможно еще большее упрощение изображения любого из маятников, которое иногда бывает необходимо для того, чтобы не отвлекать внимание обучающихся на второстепенные (не важные в данном контексте) детали изображения.
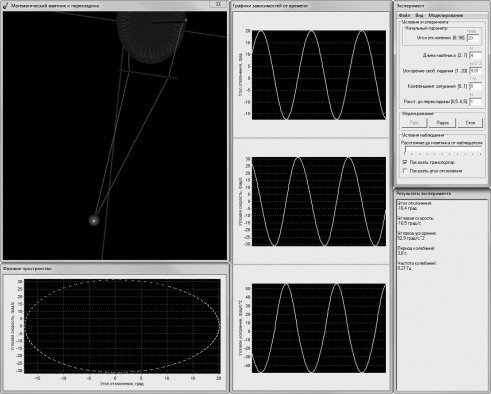
Рис. 3. Учебная компьютерная модель маятника с бифилярным подвесом
Все программы предполагают следующую (общую для всех) последовательность осуществления операций обучающимся. Сначала обучающийся задает начальные условия колебательной системы и внешние условия среды, в которой она находится. При этом модель статична, ее параметры остаются неизменными. После того, как нужные исследователю условия заданы, модель переводится в динамическое состояние — начинается ее движение. В ходе этого движения осуществляется наблюдение за моделью, причем не только за ее наглядным образом, но и за ее характеристиками, зависимости которых от времени выводятся синхронно с движением маятника. Это способствует тому, что обучающийся сопоставляет конкретные положения маятника (или его частей) с конкретным видом соответствующих графиков зависимостей координаты, скорости или ускорения от времени. Кроме того, в специальном окне выводятся текущие (мгновенные) значения этих величин, которые можно лучше увидеть и запомнить в режиме паузы, который специально предусмотрен для такого случая.
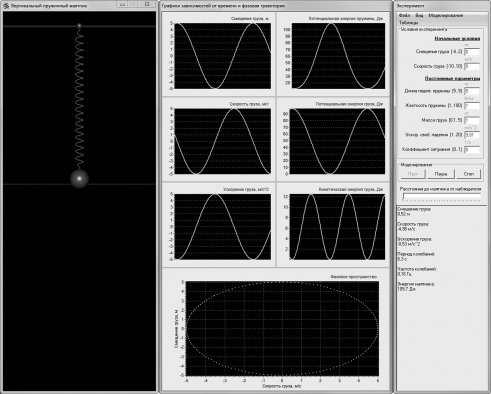
Рис. 4. Учебная компьютерная модель пружинного маятника
Обучающийся имеет возможность экспериментировать с моделями таким образом, что позволяет ему обнаружить некоторые связи между ними. Например, исследуя модель физического маятника (рис. 7), он может убедиться, что при определенных условиях (при массах одного из грузов и стержня равных нулю), получается система, абсолютно похожая на математический маятник (рис. 1). Также он может убедиться, что системы, изображенные на рис. 2 и рис. 5, при некоторых заданных параметрах, идентичны системам, изображенным на рис. 1 и рис. 4 соответственно.
Модели пружинных маятников (рис. 4 и 5) позволяют еще и проследить закономерность, которая носит фундаментальный характер и называется законом сохранения полной механической энергии, в режиме «реального времени». В приложениях, реализующих эти модели, предусмотрено окно для вывода графиков зависимостей от времени потенциальной, кинетической и полной механической энергии колебательной системы.
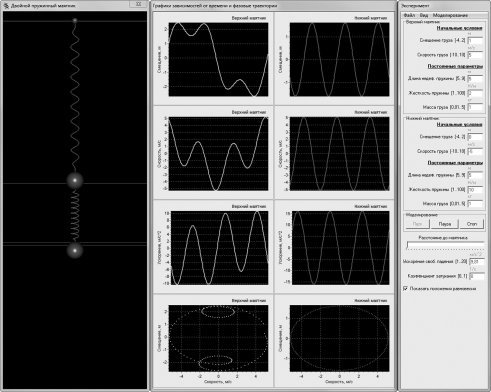
Рис. 5. Учебная компьютерная модель двойного пружинного маятника
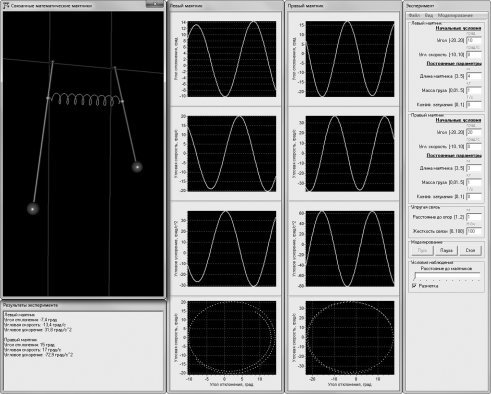
Рис. 6. Учебная компьютерная модель двух упруго связанных математических маятников
Одним из основных мотивов применения нами в обучении представленного в статье компьютерного (вычислительного) эксперимента для изучения физических систем является устранение в нем ограничений, присущих аналитическим моделям. Исследуя компьютерные модели, обучающийся получает возможность изучать сложные модели, которые нельзя изучить с помощью аналитических методов [1, с. 5–6]. Таким образом, компьютерный эксперимент является своеобразным эталоном, с которым можно сравнивать те или иные теоретические модели. К тому же, его проведение не исключает сравнение его результатов с результатами натурного эксперимента. При этом может осуществляться проверка валидности используемой модели [3, с. 20–21].
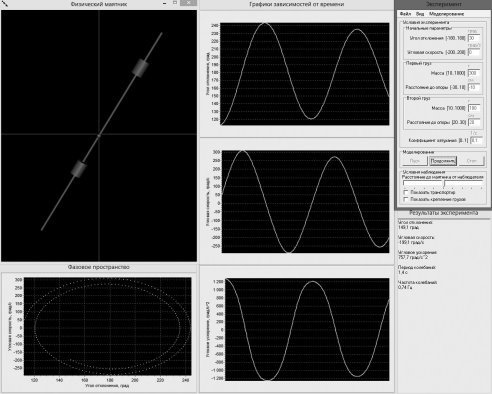
Рис. 7. Учебная компьютерная модель физического маятника
Литература:
- Бутиков Е. И. Физика колебаний: Лаборатория компьютерного моделирования: Учебное пособие / Е. И. Бутиков. — СПб.: Санкт-Петербургский государственный университет, 2008. — 150 с.
- Данилов О. Е. Использование компьютерных моделей маятников при изучении механических колебаний / О. Е. Данилов // Дистанционное и виртуальное обучение. — 2015. — № 7. — С. 40–47.
- Данилов О. Е. Решение задач механики с помощью компьютерных моделей / О. Е. Данилов // Дистанционное и виртуальное обучение. — 2015. — № 3. — С. 40–48.
- Хеерман Д. В. Методы компьютерного эксперимента в теоретической физике: Пер. с англ. / Д. В. Хеерман; Под ред. С. А. Ахманова. — М.: Наука, Гл. ред. физ.-мат. лит., 1990. — 176 с.







