Инжиниринг трафика в программно определяемых сетях

В статье рассматривается проблема развертывания программно-определяемых компонент в уже существующую сеть. Дается формулировка проблемы оптимизации контроллера программно определяемой сети и математическое описание на основе прямо-двойственного алгоритма.

 

Программно-определяемая сеть — это идеология построения сети, в которой разделены уровень управления сетью и уровень пересылки пакетов. Общим для всех подходов построения программно-определяемых является то, что программно-определяемая сеть состоит из двух основных компонентов:

‒  Контроллер программно-определяемой сети (КС). КС представляет собой логически централизованную функцию [1], [2]. Сеть, как правило, контролируется одним или несколькими КС. КС определяет путь пересылки для каждого потока в сети;

‒  Элемент пересылки программно-определяемой сети (ЭП). ЭП образуют уровень передачи данных в сети. Логика пересылки пакетов определяется КС и реализуется в таблице пересылки.

Проблема инжиниринга трафика заключается в том, что в вероятном сценарии программно-определяемые компоненты будут постепенно развертываться в уже существующей сети. В такой сети не обязательно весь трафик управляется одним КС. Там может быть несколько КС для различных частей сети, а также некоторые части сети могут использовать уже существующую маршрутизацию в сети. Ключевой вопрос заключается в том, что еще можно сделать эффективным в управлении трафиком, когда весь трафик в сети не может управляться централизованно одним КС.

1. Описание системы

Рассматриваемаясеть содержит центральный КС, который вычисляет таблицы маршрутизации для ряда ЭП. Предполагается, что ЭП представляют собой подмножество узлов в сети. Остальные узлы в сети запускают некоторый стандартный hop-by-hop протокол маршрутизации (например OSPF). КС просматривает сеть и собирает информацию о состоянии канала связи. Пакеты маршрутизации ЭП и логика для вычисления таблицы маршрутизации на ЭП находится в централизованном КС. В дополнение к пересылке пакетов, ЭП выполняет некоторые простые измерения трафика, которые передаются КС. КС использует эту информацию о трафике вместе с информацией, распространяемой в сети с помощью протокола OSPF-TE, чтобы динамически изменять таблицы маршрутизации на ЭП с целью адаптации к изменяющимся состояниям трафика. Обычные узлы сети являются стандартными маршрутизаторами, использующими обычный hop-by-hop механизм маршрутизации [3]. Предполагается, что никакие изменения не будут внесены в обычные узлы и они могут не знать о существовании ЭП в сети.

Пример сети с КС и элементами пересылки показан на Рис. 1. Элементы пересылки в узлах 2, 9, 14 управляются КС извне. Данная сеть будет использоваться для иллюстрации концепций, выдвинутых в данной работе. Для простоты полагаем, что все соединения в сети являются двунаправленными и веса линий связи устанавливаются в единицу. Теперь опишем КС и ЭП более подробно.

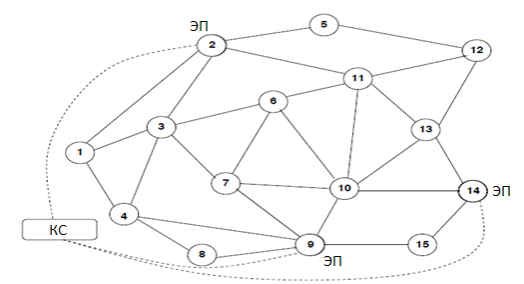
Рис. 1. Рассматриваемая сеть

 

1.1 Элемент пересылки программно-определяемой сети

ЭП выполняет следующие функции:

Пересылка: ЭП действуют в основном в качестве элементов маршрутизации. Таблица маршрутизации вычисляется на КС [4]. ЭП может обрабатывать несколько следующих переходов для данного узла назначения. Если имеется несколько следующих переходов до данного узла назначения, то ЭП может разделить трафик к месту назначения в заранее установленном порядке на несколько следующих узлов.

Измерение: Таблица маршрутизации на ЭП изменяется незначительно, по сравнению со стандартной таблицей маршрутизации для того, чтобы способствовать измерению трафика на ЭП. Схематическое изображение, показывающее разницу между стандартной таблицей маршрутизации и таблицу маршрутизации на ЭП показано в Таблица 1. В ней имеется дополнительный столбец для узла в сети, который может достичь IP-адреса назначения. Когда пакет обрабатывается ЭП он делает длинный префикс на IP-адрес назначения для определения следующего шага. Это также увеличивает счетчик, соответствующий узлу назначения по длине пакета. Это делается для того, чтобы определить объем трафика между ЭП и другими узлами в сети. Рассмотрим таблицу маршрутизации на узле 2. Предположим, что узел 15 (IP-адрес 45.67.2.5) объявляет достижимость к подсети 135.23 \ 16. Пусть узел 11 имеет IP адрес 43.2.34.7, будет следующим шагом по кратчайшему пути от узла 2 к узлу 15. Часть таблицы маршрутизации на узле 2 показана в Таблица 1. Столбец, соответствующий трафику, отслеживает число байтов маршрутизации от узла 2 к узлу 15 для префикса назначения 135.23 \ 16. ЭП также может вычислить общий трафик, отправляемый от узла 2 к узлу 15.

 

Таблица 1

Таблица маршрутизации

Префикс	Узел	Следующий узел	Трафик
135.23/16	45.67.2.5	43.2.34.7

 

1.2 Контроллер программно-определяемой сети

КС выполняет всю логику маршрутизации и координирует маршрутизацию на всех ЭП для того, чтобы достичь наилучшей производительности сети. КС выполняет следующие функции:

Просмотр: КС обменивается с другими узлами сети весами связей и другой информацией о топологии с помощью технологии OSPF-TE [5]. Поэтому КС знает текущие веса OSPF, а также количество транспортных потоков по каждой линии связи (в среднем за некоторый период времени).

Вычисление маршрута: КС отвечает за вычисление таблиц маршрутизации для всех ЭП в сети. Вычисление происходит с учетом маршрутизации, осуществляемой на обычных узлах (на основе весов линий связи OSPF), трафик по линиям связи (на основе информации OSPF-TE) и текущий шаблон трафика (на основе измерений на ЭП). Алгоритм для вычисления маршрутизации для ЭП должен гарантировать, что маршрутизация будет происходить по путям без петель при одновременной минимизации перегрузки сети.

2. Постановка задачи КС

Предположим, что сеть состоит из множества узлов , соединенных между собой с помощью множества направленных связей . Пусть – это множество ЭП, а – узлы, не являющиеся ЭП. Пусть ) и обозначает вес линии связи OSPF и пропускной способности соответственно звена , а – поток трафика на линии е. Поток на всех звеньях является доступным КС по OSPF-TE. Tsd — скорость трафика от узла до некоторого другого узла d ∈ N и Wud представляет общий объем трафика для узла назначения d ∈ N, что либо берет свое начало или проходит через ЭП е ∈ С. Можно заметить, что в общем Wud ≥ Tud. ЭП u может измерять Wud для всех адресатов d, используя расширенную таблицу маршрутизации (Таблица 1). Значение Tsd для всех пар узлов (s, d) КС не известно. Каждый узел вычисляет кратчайший путь ко всем другим узлам в сети. Таблица маршрутизации в узле u ∈ N включает в себя переход по кратчайшему пути к каждому узлу в сети. Обозначим NH (u, d) как следующий переход от узла u до узла назначения d. Другими словами, NH (u, d) является первым узлом по кратчайшему пути от u до d. Для простоты предполагаем, что следующий переход является уникальным для всех элементов, не являющихся ЭП, т. е. NH (u, d) имеет только один элемент для всех u ∈ D. Методы, содержащиеся в этой статье, распространяются на случай, когда существуют альтернативные кратчайшие пути между двумя узлами, и трафик разделяется между этими двумя путями как в равноценных путях.

Проиллюстрируем некоторые из концепций, изложенных в предыдущем параграфе, используя Рис. 2. Предполагаем, что все веса равны единице и сплошные связи представляют дерево кратчайших путей к узлу 13. Напомним, что узлы 2, 9, 14 являются ЭП. Следует отметить, что NH (6, 13) = 10, NH (1, 13) = 2 и так далее. Пунктирные линии показывают альтернативные пути, возможные из ЭП. Например, узел 2 может разделить трафик на узел 13 по двум различным переходам, один собирается на узел 5, а другой на узел 11.

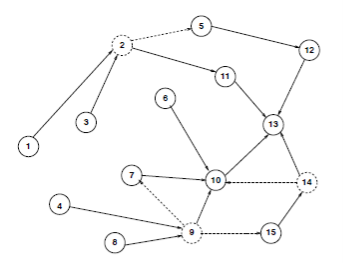
Рис. 2. Дерево кратчайших путей до узла 13

 

Определение 1: С учетом набора из С ЭП, путь s=u0,u1,u2,...uk = d от узла-источника s до узла назначения d будет называться выполнимым, если при j=1,2,...,k, (uj-1,uj) ∈ E и

Выполнимый путь, где u0,u1,u2,...uk различны, называется допустимым путем. Обозначим Psd как множество допустимых путей между s и d.

Из определения следует, что путь представляется возможным, если следующий переход к заданному узлу назначения для всех обычных элементов сети задается алгоритмом нахождения кратчайшего пути. Далее выполнимый путь допустим, только при отсутствии петель. Поэтому нужно убедиться, что весь трафик между s и d должен быть направлен на P ∈ Psd.

Например, на Рис. 2, 3–2-5–12–13 представляет собой допустимый путь от 3 до 13. Заметим, что это не самый короткий путь, которым является 3–2-11–13. Путь 3–6-11–13 не допустим, так как следующим шагом для узла 3, который не является ЭП, должен быть следующий шаг по кратчайшему пути, которым является узел 2.

Определение 2: Учитывая кратчайший путь маршрутизации на обычном узле, трафик, который идет от источника к месту назначения без транзита через ЭП будет называться неконтролируемым. Если источником пакета является ЭП, или если он проходит по крайней мере через один ЭП, прежде чем он достигнет своего назначения, то этот трафик будет называться контролируемым.

Другими словами, контролируемый трафик состоит из пакетов, которые проходят через, по меньшей мере, один ЭП. Например, трафик от 6 до 13 направляется на OSPF по 6–10–13, и так как ни 6, ни 10 являются ЭП, трафик от узла 6 до узла 13 не контролируется. В отличие от этого, трафик от узла 8 до 13 проходит через узел 9, который является ЭП и, следовательно, этот трафик является контролируемым.

Определение 3: Будем говорить, что ЭП u∈Cвводит пакет, если

‒  Узел u находится на пути маршрутизации OSPF для пакета;

‒  Пакет проходит через u раньше, чем он проходит через любой другой ЭП.

Трафик, который вводится с помощью ЭП u ∈ C для некоторого узла назначения d ∈ N, будем обозначать Iud.

Поэтому для всего контролируемого трафика есть уникальный ЭП, который вводит этот трафик. Поясним это на Рис. 3. На этом рисунке номер рядом с узлом представляет собой скорость трафика от этого узла к узлу 13. Например, трафик от узла 1 к узлу 13 (T1,13) равен 3 единицы. По определению 3 трафик от 3 до 13 будет вводиться с помощью ЭП-2. Например, на рисунке 3, I2,13 = 9, I9,13 = 13 и I14,13 = 5. Как отмечалось ранее, значения Tsd не известны КС. Измерениями, доступными на КС, являются значения Wud, которыми является трафик для назначения d, который проходит через узел u ∈ C.

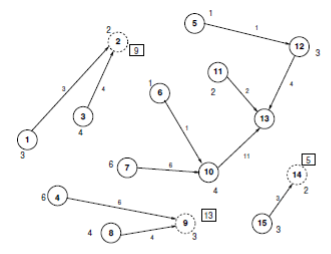
Рис. 3. Независимый трафик на ЭП

 

3. Формулировка проблемы КС

Поскольку контролируемым является трафик, который проходит через ЭП, нужно рассмотреть трафик, вводимый на ЭП. Трафик Iud, вводимый на ЭП u ∈ С, должен достичь назначения d. Это возможно только по одному из допустимых путей P ∈ Pud. Пусть g (е) обозначает неуправляемый поток на линии е. Целью КС является построение маршрута контролируемого трафика таким образом, что задержка и потеря пакетов на линии сведены к минимуму. Одной из естественных целей для КС является минимизация максимального использования связей в сети(х(Р) — поток в пути P):

при условии

(2)

(3)

(4)

‒  Первый набор неравенств показывает, что общий поток на связь, который является суммой неконтролируемого потока (представленного по возрастанию g(e)) и контролируемого потока (который является вторым членом суммы на правой стороне) меньше, чем произведение максимального использования линии связи (θ) на пропускную способность линии связи (с (е));

‒  Второй набор неравенств показывает, что суммарный вводимый трафик направляется в сеть;

‒  Третий набор неравенств гарантирует, что поток на любом пути является неотрицательным.

Оптимальное значение θ это максимальное использование какой-либо связи. Если оптимальное значение θ <1, то ни одна из связей не будет использоваться чрезмерно. После того, как КС решает эту задачу оптимизации, то легко вычислить следующие переходы и соответствующие веса во всех ЭП для каждого пункта назначения.

В приведенной выше постановке, имело место предположение, что значения Iud и g(е) известны. На самом деле обе величины Iud, а также g(е) должны быть вычислены с помощью КС на основе измерений, сделанных ЭП, а также протокола сообщения OSPF-TE, полученных КС.

3.1 Динамическое вычисление Iud и g(e)

Измеренными величинами, которые доступны для КС являются

‒  Нагрузка связи f(е) для всех ссылок е ∈ Е, которую можно получить от OSPF-TE.

‒  Величина Wud для всех u ∈ C для всех d ∈ N. Это измеряется ЭП и передается к КС.

С помощью этих двух величин КС должен вычислять значения g(е) для всех е ∈ Е и Iud для всех u ∈ C для всех d ∈ N. Для начала нужно вычислить Iud. Рассмотрим фиксированный целевой узел d. КС знает текущий маршрут к этому узлу назначения d. Он знает все следующие переходы для всех узлов d и на всех ЭП, но не знает все следующие переходы до назначения и распределение трафика, если есть несколько вариантов маршрута.

Определение 4: Учитывая узел назначения d и текущую маршрутизацию в сети, порядок маршрутизации узловв C относительно этого d определяется как упорядочение узлов в C \ D такое, что если u ∈ C появляется перед v ∈ C в этом списке, то нет другого потока, чей пункт назначения d, который направляется от v к u. Обозначим порядок маршрутизации для узла назначения d как R (d) и тот факт, что u появляется перед v в R(d) как u ≺d v.

Этот порядок маршрутизации корректно определен для любого целевого узла d, так как там не может быть петель в маршруте трафика, проходящем по назначению d. Предположим, что текущая маршрутизация к узлу 13 происходит так, как показано на Рис. 4. Отражена только та часть маршрута, которая имеет отношение к ЭП. В этом случае нужно обратить внимание, что трафик от узла 9 проходит через узел 14. Поэтому 9 ≺13 14. Один порядок маршрутизации (2, 9, 14). Другие упорядочивания возможны, но тогда узел 14 должен появиться после того, как узел 9.

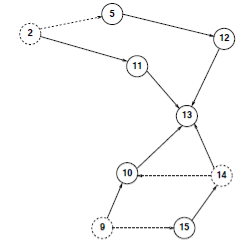
Рис. 4. Порядок маршрутизации

 

Алгоритм для вычисления значения Iud

Для каждого узла назначения d ∈ N

1.   Вычислить порядок маршрутизации R(d);
2.   Для первого узла u в R(d) установить Iud=Wud;
3.   Построить первый маршрут потока от u к d и установить βv(u, d) как часть потока, который достигает узла v ∈ C;
4.   Для каждого последующего узла w в R(d). Установить 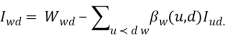Построить первый маршрут потока от w к d и установить βv(w, d) для всех v ∈ C.

После того, как значения Iud известны для всех u ∈ C для всех d ∈ N, нужно вычислить значения g (е), который является неконтролируемым трафиком, проходящим по линии е ∈ E. Это делается следующим образом: вводится единица потока в узле u ∈ C для назначения d ∈ N и вычисляется αe(u, d), которая является частью этого единичного потока, который перенаправляется на линии е. Так как Iud известно для u ∈ C, можно вычислить

(5)

КС теперь знает значения Iud для всех узлов u ∈ C для всех d ∈ N, а также значения g(е) для всех е ∈ E.

3.2 Формулировка проблемы динамической маршрутизации

Необходимо провести маршрутизацию трафика КС, чтобы минимизировать максимальное использование связей в сети. Эквивалентная проблема, которую более удобно решить, это задать пропускную способность линии фиксированной, но изменять вводимый трафик таким образом, что он по-прежнему помещался в сети. Эта проблема заключается в следующем:

при условии

(6)

(7)

(8)

Если оптимальное λ>1, то текущий трафик может быть направлен на ЭП, обеспечивая при этом, что все связи меньше, чем один путь использования. Несмотря на то, что проблема имеет экспоненциальное число переменных, можно решить проблему до любого желаемого уровня точности, используя прямо-двойственный алгоритм.

Для того, чтобы написать линейную программу (решение) для динамической задачи маршрутизации, показанной выше, нужно связать двойственные переменные l (e) с пропускной способностью канала связи и zud для ограничения спроса. Прямо-двойственный алгоритм теперь может быть записан в виде

при условии

(9)

(10)

(11)

Предположим, что l(e) устанавливается как вес ссылки е ∈ Е. Lud обозначим как кратчайший путь от u до d с учетом весов связей l(e) на ссылку е. Прямо-двойственный алгоритм теперь может быть переписан в виде

(12)

при условии

(13)

(14)

Другими словами, учитывая любой неотрицательный набор весов связей l(e), 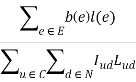является верхней границей в задаче динамической маршрутизации.

Заключение

В данной работе была рассмотрена проблема развертывания программно-определяемых компонент в существующей сети. Была сформулирована проблема контроллера программно-определяемой сети и введены понятия допустимого, выполнимого и контролируемого пути, введения трафика в сеть и порядка маршрутизации узлов. Также представлена формулировка проблемы динамической маршрутизации на контроллере программно-определяемой сети и её математическое описание на основе прямо-двойственного алгоритма.

 

Литература:

 

1. N.Gude, T.Koponen, J.Petit, B.Pfaff, M.Casado, N. McKeown, ”Nox: Towards a Network Operating System”, ACM SIGCOMM CCR.
2. T. Koponen ”Onix: A Distributed Control Platform for Large Scale Production Networks”.
3. C. Rothernberg, C. N. A. Correa, R. Raszuk ”Revisiting Routing Control Platforms with the Eyes and Muscles of Software-Defined Networking”, ACM-SIGCOMM HotSDN Workshop, 2012
4. T. V. Lakshman, T. Nandagopal, R. Ramjee, K. Sabnani, T. Woo, ”The SoftRouter Architecture”, Proceeding of Hotnets 2004
5. M. R. Nascimento, C. E. Rothenberg, M. R. Salvador, C. N. A. Correa, S. C. de Lucena, M. F. Magalhaes ”Virtual Routers as a Service: the RouteFlow approach leveraging Software-Defined Networks”, CFI 2011.