В настоящей работе найдена новая крупномасштабная неустойчивость во вращающейся стратифицированной самогравитирующей среде с мелкомасштабной турбулентностью. Турбулентность возбуждается внешней мелкомасштабной силой с нулевой спиральностью и малым числом Рейнольдса. Теория построена на основе метода многомасштабных асимптотических разложений. В пятом порядке теории возмущений получены основные уравнения, описывающие неустойчивость типа гидродинамического ![]() -эффекта во вращающейся турбулентной среде.
-эффекта во вращающейся турбулентной среде.
Ключевые слова: сила Кориолиса, многомасштабные асимптотические разложения, стратифицированная самогравитирующая среда, неспиральная мелкомасштабная турбулентность, ![]() -эффект
-эффект
In this paper we found a new large-scale instability in the rotating self-gravitating stratified medium with small-scale turbulence. Turbulence excited small-scale external force with zero helicity and low Reynolds number. The theory is based on the method of multi-scale asymptotic expansions. In the fifth-order perturbation theory the basic equations describing instability like hydrodynamic α-effect in the rotating turbulent medium are received.
Keywords: coriolis force, multiscale asymptotic expansions, self-gravitating stratified media, nonspiral small-scale turbulence, ![]() -effect
-effect
Исследование проблемы генерации крупномасштабных вихревых структур (КВС) имеет важное значение для целого ряда геофизических и астрофизических задач. В частности, к геофизическим задачам относятся исследования по генерации КВС типа тропических циклонов (тайфунов), торнадо, смерчей и т. д. Эти КВС играют большую роль в глобальной циркуляции атмосферы, что очень важно для прогноза погоды и климата на нашей планете [1–5]. К астрофизическим задачам относятся проблемы генерации КВС в галактических дисках, в атмосферах планет Солнечной системы и т. п. [6–8] Центральное место в этом направлении занимает теория вихревого динамо [5]. Первоначально идея вихревого динамо была высказана в работе [9], после того как был открыт ![]() -эффект в магнитной гидродинамике [10–16]. На основе сходства уравнений индукции магнитного поля и вихря в гидродинамике, в работе [9] была выдвинута гипотеза, что спиральная турбулентность способна генерировать крупные вихри подобно крупномасштабному магнитному полю в магнитной гидродинамике [10]. Физическая сущность этого явления заключается в инверсном каскаде передачи энергии от мелких вихрей к более крупным. Эта гипотеза была на время забыта после появления работы [17], в которой показано, что в несжимаемой жидкости со спиральной турбулентностью крупные вихри затухают на турбулентной вязкости. Результаты, полученные в [17], носят название теоремы-антидинамо, запрещающей генерацию КВС спиральной турбулентностью в несжимаемой жидкости. Несмотря на запрет теоремы-антидинамо, первый пример вихревого динамо был найден в работе [18]. Там было показано, что спиральная турбулентность в сжимаемой жидкости может усиливать крупномасштабные вихревые возмущения. Этот эффект получил название гидродинамического
-эффект в магнитной гидродинамике [10–16]. На основе сходства уравнений индукции магнитного поля и вихря в гидродинамике, в работе [9] была выдвинута гипотеза, что спиральная турбулентность способна генерировать крупные вихри подобно крупномасштабному магнитному полю в магнитной гидродинамике [10]. Физическая сущность этого явления заключается в инверсном каскаде передачи энергии от мелких вихрей к более крупным. Эта гипотеза была на время забыта после появления работы [17], в которой показано, что в несжимаемой жидкости со спиральной турбулентностью крупные вихри затухают на турбулентной вязкости. Результаты, полученные в [17], носят название теоремы-антидинамо, запрещающей генерацию КВС спиральной турбулентностью в несжимаемой жидкости. Несмотря на запрет теоремы-антидинамо, первый пример вихревого динамо был найден в работе [18]. Там было показано, что спиральная турбулентность в сжимаемой жидкости может усиливать крупномасштабные вихревые возмущения. Этот эффект получил название гидродинамического ![]() -эффекта. Его появление обусловлено нарушением симметрии в тензоре напряжений Рейнольдса из-за сжимаемости среды. В дальнейшем были найдены другие факторы нарушения симметрии уравнений, такие как неоднородный поток [19], градиент температуры в поле тяжести [20], частицы примеси и пузырьки воздуха в среде [19]. Известно также большое количество работ по генерации КВС с учетом эффектов вращения [21–28].
-эффекта. Его появление обусловлено нарушением симметрии в тензоре напряжений Рейнольдса из-за сжимаемости среды. В дальнейшем были найдены другие факторы нарушения симметрии уравнений, такие как неоднородный поток [19], градиент температуры в поле тяжести [20], частицы примеси и пузырьки воздуха в среде [19]. Известно также большое количество работ по генерации КВС с учетом эффектов вращения [21–28].
На начальном этапе развития теории динамо, замкнутые уравнения для средних (крупномасштабных) полей были получены в основном при помощи метода электродинамики среднего поля (или теории корреляционного сглаживания второго порядка) [10] и функциональной техники [29, 30]. Оба эти метода в применении к задачам теории динамо имеют главный недостаток, заключающийся в трудности определения из всей иерархии возмущений главного порядка, при котором возникает неустойчивость. В связи с этим, в работе [31] была рассмотрена крупномасштабная неустойчивость в несжимаемой жидкости методом асимптотических многомасштабных разложений. В качестве малого параметра для асимптотического метода многомасштабных разложений используется число Рейнольдса ![]() для мелкомасштабных пульсаций скорости
для мелкомасштабных пульсаций скорости ![]() , вызванных мелкомасштабной силой. Модель внешней мелкомасштабной силы была выбрана с нарушением четности (при нулевой спиральности). Эффект генерации крупномасштабных возмущений такой силой получил название анизотропного кинетического альфа-эффекта или АКА-эффекта [31]. Отметим, что нарушение четности является наиболее общим понятием, чем спиральность, хотя именно спиральность
, вызванных мелкомасштабной силой. Модель внешней мелкомасштабной силы была выбрана с нарушением четности (при нулевой спиральности). Эффект генерации крупномасштабных возмущений такой силой получил название анизотропного кинетического альфа-эффекта или АКА-эффекта [31]. Отметим, что нарушение четности является наиболее общим понятием, чем спиральность, хотя именно спиральность ![]() является самым распространенным механизмом нарушения четности гидродинамических течений. В дальнейшем, применяя метод многомасштабных асимптотических разложений, были разработаны линейные и нелинейные теории вихревого динамо для сжимаемых сред [32, 33], конвективных сред со спиральной внешней силой [34, 35]. Во всех упомянутых выше работах спиральная турбулентность считалась заданной, либо вопрос о ее происхождении (генерации) рассматривался отдельно [36]. Генерацию спиральной турбулентности в природных условиях обычно связывают с влиянием силы Кориолиса (или силы Лоренца) на турбулентное движение среды [10, 36], которое изначально было однородным изотропным и зеркально-симметричным (неспиральным). Отсюда естественно возникает вопрос о возможности генерации крупномасштабных полей (вихревых и магнитных) во вращающихся средах под действием мелкомасштабной силы с нулевой спиральностью
является самым распространенным механизмом нарушения четности гидродинамических течений. В дальнейшем, применяя метод многомасштабных асимптотических разложений, были разработаны линейные и нелинейные теории вихревого динамо для сжимаемых сред [32, 33], конвективных сред со спиральной внешней силой [34, 35]. Во всех упомянутых выше работах спиральная турбулентность считалась заданной, либо вопрос о ее происхождении (генерации) рассматривался отдельно [36]. Генерацию спиральной турбулентности в природных условиях обычно связывают с влиянием силы Кориолиса (или силы Лоренца) на турбулентное движение среды [10, 36], которое изначально было однородным изотропным и зеркально-симметричным (неспиральным). Отсюда естественно возникает вопрос о возможности генерации крупномасштабных полей (вихревых и магнитных) во вращающихся средах под действием мелкомасштабной силы с нулевой спиральностью ![]() . Такой пример генерации КВС во вращающейся несжимаемой жидкости был найден в работе [27]. Там же было показано, что в результате развития крупномасштабной неустойчивости в наклонно вращающейся жидкости возникают нелинейные крупномасштабные спиральные вихревые структуры типа вихрей Бельтрами или локализованные кинки с внутренней спиральной структурой.
. Такой пример генерации КВС во вращающейся несжимаемой жидкости был найден в работе [27]. Там же было показано, что в результате развития крупномасштабной неустойчивости в наклонно вращающейся жидкости возникают нелинейные крупномасштабные спиральные вихревые структуры типа вихрей Бельтрами или локализованные кинки с внутренней спиральной структурой.
В настоящей работе исследуется генерация КВС в стратифицированной вращающейся среде с учетом ее самогравитации и сжимаемости под действием мелкомасштабной неспиральной силы. В отличие от работы [27], выбрана декартовая система координат для вращающейся среды, в которой вектор угловой скорости вращения ![]() направлен вдоль вертикальной оси
направлен вдоль вертикальной оси ![]() . Такая постановка проблемы связана с возможным астрофизическим приложением задачи. Полученный в работе инкремент крупномасштабной неустойчивости соответствует гидродинамическо
. Такая постановка проблемы связана с возможным астрофизическим приложением задачи. Полученный в работе инкремент крупномасштабной неустойчивости соответствует гидродинамическо ![]() -эффекту, который возникает в результате совместного действия неспиральной силы, вращения и стратификации среды. На основе метода многомасштабных асимптотических разложений построена линейная теория крупномасштабной неустойчивости. В результате развития этой неустойчивости типа
-эффекту, который возникает в результате совместного действия неспиральной силы, вращения и стратификации среды. На основе метода многомасштабных асимптотических разложений построена линейная теория крупномасштабной неустойчивости. В результате развития этой неустойчивости типа ![]() -эффекта генерируются КВС. Полученные в настоящей работе результаты могут найти применение к ряду астрофизических задач.
-эффекта генерируются КВС. Полученные в настоящей работе результаты могут найти применение к ряду астрофизических задач.
Основные уравнения ипостановка задачи.
Рассмотрим уравнения движения вязкой сжимаемой вращающейся среды с учетом самогравитации, которые, как известно, описываются следующей системой уравнений:
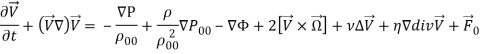 (1)
(1)
![]() (2)
(2)
![]() (3)
(3)
Здесь ![]() ,
, ![]() , P,
, P, ![]() — возмущения скорости, плотности, давления и гравитационного потенциала среды относительно равновесного состояния:
— возмущения скорости, плотности, давления и гравитационного потенциала среды относительно равновесного состояния:
![]() (4)
(4)
где ![]() — радиус-вектор элемента среды. Коэффициенты
— радиус-вектор элемента среды. Коэффициенты ![]() и
и ![]() соответствуют первой и второй кинематической вязкости для сжимаемой среды,
соответствуют первой и второй кинематической вязкости для сжимаемой среды, ![]() — коэффициенты динамической вязкости,
— коэффициенты динамической вязкости, ![]() – гравитационная постоянная. С целью упрощения вычислений выберем декартовую геометрию задачи, для которой вектор угловой скорости
– гравитационная постоянная. С целью упрощения вычислений выберем декартовую геометрию задачи, для которой вектор угловой скорости ![]() считаем постоянным и направленным вдоль оси
считаем постоянным и направленным вдоль оси ![]() вертикально вверх (
вертикально вверх (![]() – единичный вектор по вертикали). Уравнения (1)-(3) дополним уравнением состояния среды, которое для простоты выберем в виде:
– единичный вектор по вертикали). Уравнения (1)-(3) дополним уравнением состояния среды, которое для простоты выберем в виде:
![]() (5)
(5)
Здесь ![]() – скорость звука. Уравнение равновесия (4), используя (5), перепишем в следующем виде:
– скорость звука. Уравнение равновесия (4), используя (5), перепишем в следующем виде:
![]() (6)
(6)
Здесь ![]() ,
, ![]() , где
, где ![]() =
=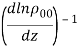 – характерный масштаб неоднородности или стратификации среды, которая возникает естественным образом в поле гравитации. Выбор обозначений для равновесного состояния (индекс с двумя нулями) связан с избежанием путаницы при использовании обозначений асимптотических разложений далее. В уравнение (1) включена внешняя сила
– характерный масштаб неоднородности или стратификации среды, которая возникает естественным образом в поле гравитации. Выбор обозначений для равновесного состояния (индекс с двумя нулями) связан с избежанием путаницы при использовании обозначений асимптотических разложений далее. В уравнение (1) включена внешняя сила ![]() , моделирующая источник возбуждения в среде мелкомасштабных и высокочастотных флуктуаций поля скорости
, моделирующая источник возбуждения в среде мелкомасштабных и высокочастотных флуктуаций поля скорости ![]() с малым числом Рейнольдса
с малым числом Рейнольдса ![]() . В отличие от предыдущих исследований [21-26, 28], здесь мы рассмотрим неспиральную внешнююсилу
. В отличие от предыдущих исследований [21-26, 28], здесь мы рассмотрим неспиральную внешнююсилу ![]() со следующими свойствами:
со следующими свойствами:
![]() (8)
(8)
где ![]() – характерный масштаб,
– характерный масштаб, ![]() – характерное время,
– характерное время, ![]() – характерная амплитуда. Очевидно, что топологические свойства поля скорости
– характерная амплитуда. Очевидно, что топологические свойства поля скорости ![]() для невращающейся среды (
для невращающейся среды (![]() будут определяться условиями (7). Далее будет показано, что при учете вращения среды (
будут определяться условиями (7). Далее будет показано, что при учете вращения среды (![]() поле скорости
поле скорости ![]() уже не обладает тривиальной топологией, т. е. средняя спиральность отлична от нуля
уже не обладает тривиальной топологией, т. е. средняя спиральность отлична от нуля ![]() . Для удобства перейдем в уравнениях (1)-(8) к безразмерным переменным:
. Для удобства перейдем в уравнениях (1)-(8) к безразмерным переменным:
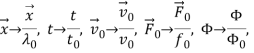
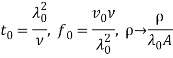 ,
, ![]() ,
, ![]() ,
, ![]()
Будем считать, что внешняя сила ![]() возбуждает такие пульсации скорости
возбуждает такие пульсации скорости ![]() , которые будут много меньше характерной скорости звука
, которые будут много меньше характерной скорости звука ![]() , иначе говоря число Маха
, иначе говоря число Маха ![]() . Далее проводя замену плотности
. Далее проводя замену плотности ![]() на
на ![]() и приняв допущение
и приняв допущение ![]() получим искомую систему уравнений:
получим искомую систему уравнений:
![]() (9)
(9)
![]() (10)
(10)
![]() (11)
(11)
где ![]() – параметр стратификации на масштабе
– параметр стратификации на масштабе ![]() ,
, ![]() ,
, ![]() – частота Джинса [6, 7]. Характер эволюции полей, описываемых системой уравнений (9)-(11), в значительной степени будет определяться следующими безразмерными параметрами:
– частота Джинса [6, 7]. Характер эволюции полей, описываемых системой уравнений (9)-(11), в значительной степени будет определяться следующими безразмерными параметрами: 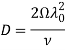 – безразмерный параметр вращения на масштабе
– безразмерный параметр вращения на масштабе ![]() , связанный с числом Тейлора
, связанный с числом Тейлора ![]() , и являющийся характеристикой степени влияния сил Кориолиса над вязкими силами. Малым параметром асимптотического разложения считаем число Рейнольдса
, и являющийся характеристикой степени влияния сил Кориолиса над вязкими силами. Малым параметром асимптотического разложения считаем число Рейнольдса ![]() , а параметр
, а параметр ![]() произвольным, не влияющими на схему разложения. Мелкомасштабная сила и внешний источник вызывают мелкомасштабные и высокочастотные флуктуации полей на фоне равновесного состояния. Средние значения таких флуктуаций нулевые, но из-за нелинейного взаимодействия в некоторых порядках теории возмущения возникают члены, которые при усреднении не обращаются в нуль. Такие члены называются секулярными и они будут условием разрешимости многомасштабного асимптотического разложения. Нахождение уравнений разрешимости, т. е. уравнений для крупномасштабных возмущений, и является основной задачей. Метод многомасштабных асимптотических разложений позволяет получить уравнения для крупномасштабных возмущений, исключая секулярные вклады в асимптотических уравнениях. Методика построения асимптотических уравнений хорошо развита в работах [5, 31, 34, 35], поэтому, избегая громоздких технических преобразований уравнений, изложим данную методику последовательно. Для этого представим пространственные и временные производные в уравнениях (9)-(11) в виде асимптотического разложения:
произвольным, не влияющими на схему разложения. Мелкомасштабная сила и внешний источник вызывают мелкомасштабные и высокочастотные флуктуации полей на фоне равновесного состояния. Средние значения таких флуктуаций нулевые, но из-за нелинейного взаимодействия в некоторых порядках теории возмущения возникают члены, которые при усреднении не обращаются в нуль. Такие члены называются секулярными и они будут условием разрешимости многомасштабного асимптотического разложения. Нахождение уравнений разрешимости, т. е. уравнений для крупномасштабных возмущений, и является основной задачей. Метод многомасштабных асимптотических разложений позволяет получить уравнения для крупномасштабных возмущений, исключая секулярные вклады в асимптотических уравнениях. Методика построения асимптотических уравнений хорошо развита в работах [5, 31, 34, 35], поэтому, избегая громоздких технических преобразований уравнений, изложим данную методику последовательно. Для этого представим пространственные и временные производные в уравнениях (9)-(11) в виде асимптотического разложения:
![]() ,
, ![]() (12)
(12)
где
![]()
![]()
![]() (13)
(13)
Подставляя разложения (12), (13) в систему уравнений (9)-(11) и собирая вместе члены с одинаковыми порядками по ![]() до степени
до степени ![]() включительно, получим уравнения многомасштабного асимптоматического разложения. Алгебраическая структура уравнений многомасштабного асимптотического разложения имеет довольно громоздкий вид. Поэтому приведем основную систему секулярных уравнений для описания эволюции крупномасштабных возмущений, которая получается в пятом порядке по
включительно, получим уравнения многомасштабного асимптоматического разложения. Алгебраическая структура уравнений многомасштабного асимптотического разложения имеет довольно громоздкий вид. Поэтому приведем основную систему секулярных уравнений для описания эволюции крупномасштабных возмущений, которая получается в пятом порядке по ![]() теории возмущений:
теории возмущений:
![]() (14)
(14)
![]() (15)
(15)
![]() (16)
(16)
В уравнениях (14)-(16) чертой сверху обозначено усреднение по быстрым переменным. Эти уравнения дополняются секулярными уравнениями, полученными в других порядках по ![]() :
:
![]() ,
, ![]() ,
, ![]() ,
, ![]()
![]() ,
, ![]() (17)
(17)
![]() ,
, ![]() ,
, ![]() (18)
(18)
Условие
![]() (19)
(19)
Для исследования устойчивости малых крупномасштабных возмущений в уравнениях (14)-(16) можно пренебречь нелинейными членами. В итоге упрощенная система уравнений, описывающая эволюцию крупномасштабных возмущений, принимает вид:
![]() (20)
(20)
![]() (21)
(21)
![]() (22)
(22)
![]() (23)
(23)
![]() (24)
(24)
Поскольку нас интересует проблема генерации крупномасштабных вихревых движений во вращающейся среде с мелкомасштабными и высокочастотными флуктуациями, то нам необходимо получить уравнения (20)-(21) в замкнутом виде. Для этой цели нужно вычислить корреляторы:
![]() (25)
(25)
![]() (26)
(26)
Их вычисление легко осуществить используя решения полученных уравнений для мелкомасштабных полей в нулевом и во втором порядках по
Замкнутые уравнения для крупномасштабных полей.
Для вычислений мелкомасштабных полей нулевого порядка ![]() необходимо детерминированным образом задать вид внешней неспиральной силы
необходимо детерминированным образом задать вид внешней неспиральной силы ![]() . В целях упрощения расчетов, выберем неспиральную внешнюю силу
. В целях упрощения расчетов, выберем неспиральную внешнюю силу ![]() , удовлетворяющую условиям (7), в следующем виде:
, удовлетворяющую условиям (7), в следующем виде:
![]() (27)
(27)
где ![]() – амплитуда внешней силы,
– амплитуда внешней силы, ![]() ,
, ![]() ,
, ![]() . Далее, для простоты расчетов будет принято:
. Далее, для простоты расчетов будет принято:
![]() [5, 34, 35]. Вид внешней силы
[5, 34, 35]. Вид внешней силы ![]() (27) можно записать в комплексной форме:
(27) можно записать в комплексной форме:
![]() (28)
(28)
которая и будет использоваться в дальнейших вычислениях. Используя определение (28), получим следующие выражения для компонент поля скорости ![]()
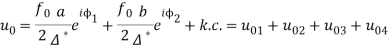 (29)
(29)
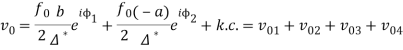 (30)
(30)
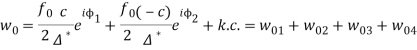 (31)
(31)
Здесь
и введены обозначения:
![]() ,
, ![]()
![]() ,
, ![]() ,
, 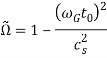 ,
, ![]() (32)
(32)
Интересно отметить, что найденное в настоящем разделе мелкомасштабное поле скорости ![]() имеет нетривиальную топологию, обусловленную вращением среды. Важной топологической характеристикой поля скорости является спиральность
имеет нетривиальную топологию, обусловленную вращением среды. Важной топологической характеристикой поля скорости является спиральность ![]() :
:
![]() (33)
(33)
которая определяется как мера «заузленности» силовых линий поля ![]() [2]. Подставляя значения (29)-(31) в формулу (33) находим:
[2]. Подставляя значения (29)-(31) в формулу (33) находим:
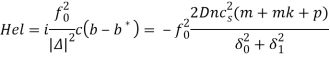 (34)
(34)
Отсюда видно, что спиральность мелкомасштабного поля скорости во вращающейся самогравитирующей среде появляется при наличии стратификации ![]() . Кроме того, генерация спиральности вращением среды предполагает появление гидродинамического
. Кроме того, генерация спиральности вращением среды предполагает появление гидродинамического ![]() -эффекта в самогравитирующей среде, ответственного за генерацию крупномасштабных вихрей. Структура полей
-эффекта в самогравитирующей среде, ответственного за генерацию крупномасштабных вихрей. Структура полей ![]() (второго порядка по
(второго порядка по ![]() ) состоит также из четырех слагаемых:
) состоит также из четырех слагаемых:
![]()
![]() (35)
(35)
Приведем явный вид слагаемых в формулах (35):
![]()
![]() ;
;
![]()
![]() (36)
(36)
![]()
![]()
![]()
![]()
![]() (37)
(37)
![]()
![]()
![]()
![]() (38)
(38)
где введены следующие обозначения:
![]() (39)
(39)
![]() (40)
(40)
В результате подстановки выше приведенных соотношений (29)-(31) и (35) в систему уравнений (20)-(21) получим замкнутую систему уравнений, которая описывает эволюцию крупномасштабных полей скорости ![]() :
:
![]() (41)
(41)
![]() (42)
(42)
Система уравнений (41)-(42) описывает динамику крупномасштабных возмущений малой амплитуды, что справедливо в рамках линейной теории. Коэффициент ![]() отвечает за конвективный перенос крупномасштабных возмущений, а посредством коэффициента
отвечает за конвективный перенос крупномасштабных возмущений, а посредством коэффициента ![]() устанавливается положительная обратная связь в результате которой возможна генерация вихревых структур. Выражения для коэффициентов
устанавливается положительная обратная связь в результате которой возможна генерация вихревых структур. Выражения для коэффициентов ![]() и
и ![]() (при
(при ![]() и
и ![]() ) имеют вид:
) имеют вид:
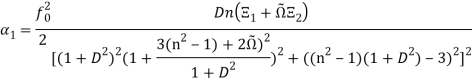 (43)
(43)
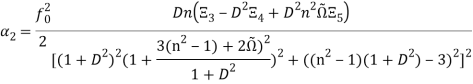 (44)
(44)
Здесь введены следующие обозначения для ![]() :
:
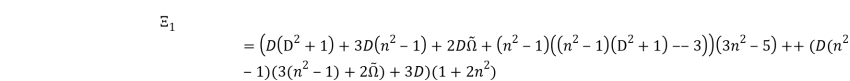 (45)
(45)
![]()
![]() (46)
(46)
![]()
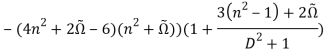 (47)
(47)
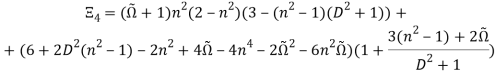 (48)
(48)
![]() (49)
(49)
В «резонансном» случае ![]() , и для стратификации среды, когда
, и для стратификации среды, когда ![]() или
или ![]() коэффициенты
коэффициенты ![]() и
и ![]() имеют самый простой вид:
имеют самый простой вид:
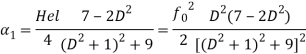
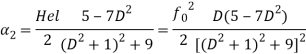 (50)
(50)
Таким образом, из полученных выше результатов можно сделать вывод, что в самогравитирующей среде возможен гидродинамический ![]() -эффект в результате действия неспиральной силы, вращения и стратификации среды.
-эффект в результате действия неспиральной силы, вращения и стратификации среды.
Крупномасштабная неустойчивость и генерация вихревых структур.
Рассмотрим начальную стадию эволюции возмущений ![]() и
и ![]() . Для исследования крупномасштабной неустойчивости, описываемой уравнениями (41)-(42), выберем возмущения в виде плоских волн с волновым вектором
. Для исследования крупномасштабной неустойчивости, описываемой уравнениями (41)-(42), выберем возмущения в виде плоских волн с волновым вектором ![]() :
:
Подставив (51) в уравнения (41)-(42) получим дисперсионное уравнение:
![]() (52)
(52)
Представив ![]() из уравнения (52) находим:
из уравнения (52) находим:
![]() (53)
(53)
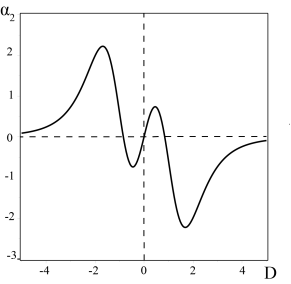
Рис. 1. График зависимости ГД ![]() -эффекта от вращения среды (параметра
-эффекта от вращения среды (параметра ![]() ) при
) при ![]() и
и ![]()
![]() (54)
(54)
Реальная часть ![]() указывает на колебания крупномасштабных возмущений, а мнимая часть
указывает на колебания крупномасштабных возмущений, а мнимая часть ![]() - на усиление (или затухание) крупномасштабных возмущений, которые возникают во вращающейся среде. Для нашей задачи представляет наибольший интерес анализ инкремента неустойчивости
- на усиление (или затухание) крупномасштабных возмущений, которые возникают во вращающейся среде. Для нашей задачи представляет наибольший интерес анализ инкремента неустойчивости ![]() , и как следствие, исследование физических свойств коэффициента
, и как следствие, исследование физических свойств коэффициента ![]() от параметров среды:
от параметров среды: ![]() . В результате проведенных исследований было установлено, что на коэффициент усиления
. В результате проведенных исследований было установлено, что на коэффициент усиления ![]() эффект вращения оказывает максимальное влияние, если безразмерные параметры стратификации и самогравитации соответственно равны:
эффект вращения оказывает максимальное влияние, если безразмерные параметры стратификации и самогравитации соответственно равны: ![]() и
и ![]() или
или ![]() . Для этого случая график зависимости коэффициента
. Для этого случая график зависимости коэффициента ![]() от параметра вращения
от параметра вращения ![]() изображен на Рис. 1. Как видно из Рис. 1, при увеличении значения параметра
изображен на Рис. 1. Как видно из Рис. 1, при увеличении значения параметра ![]() от
от ![]() до
до ![]() мы наблюдаем рост значений
мы наблюдаем рост значений ![]() до максимального значения
до максимального значения ![]() для
для ![]() . В интервале
. В интервале ![]() происходит спад величины
происходит спад величины ![]() в область отрицательных чисел, и проходя нулевую отметку
в область отрицательных чисел, и проходя нулевую отметку ![]() при
при ![]() , достигает своего минимального уровня
, достигает своего минимального уровня ![]() с параметром вращения
с параметром вращения ![]() . Далее при увеличении эффекта вращения (
. Далее при увеличении эффекта вращения (![]() ) мы наблюдаем стремление
) мы наблюдаем стремление ![]() , или подавление ГД
, или подавление ГД ![]() - эффекта. Подобное явление было описано в работе [37]. Антисимметричная зависимость
- эффекта. Подобное явление было описано в работе [37]. Антисимметричная зависимость ![]() от параметра вращения
от параметра вращения ![]() позволяет перенести сделанные выше выводы для области отрицательных значений проекции
позволяет перенести сделанные выше выводы для области отрицательных значений проекции ![]() в обратном порядке. Инкремент неустойчивости (
в обратном порядке. Инкремент неустойчивости (![]() (см. Рис. 2) имеет вид известного из линейной теории динамо [9-16,18-20]
(см. Рис. 2) имеет вид известного из линейной теории динамо [9-16,18-20] ![]() - эффекта. Максимальное значение инкремент неустойчивости
- эффекта. Максимальное значение инкремент неустойчивости 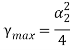 достигает при
достигает при ![]() .
.
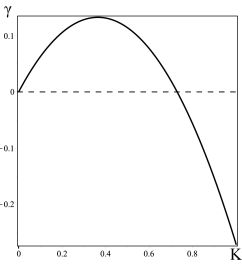
Рис. 2. График зависимости инкремента неустойчивости ![]() от волновых чисел
от волновых чисел ![]()
Заключение.
Применяя асимптотический метод многих масштабов получен новый тип крупномасштабной неустойчивости во вращающейся стратифицированной среде с самогравитацией при наличии мелкомасштабных осцилляций с нулевой спиральностью. Определены условия максимального роста вихревых возмущений в результате генерации средней спиральности ![]() вращением среды. Наибольший вклад эфффекта вращения в величину средней спиральности достигается при наличии связи характеристик среды с характерными масштабами осцилляций:
вращением среды. Наибольший вклад эфффекта вращения в величину средней спиральности достигается при наличии связи характеристик среды с характерными масштабами осцилляций: ![]() . В заключении приведем количественные оценки характерных масштабов и времен крупномасштабной неустойчивости гидродинамического
. В заключении приведем количественные оценки характерных масштабов и времен крупномасштабной неустойчивости гидродинамического ![]() -эффекта на примере галактической среды. Максимальное значение для инкремента неустойчивости вихревых возмущений:
-эффекта на примере галактической среды. Максимальное значение для инкремента неустойчивости вихревых возмущений: ![]() , а соответствующий характерный масштаб неустойчивой моды:
, а соответствующий характерный масштаб неустойчивой моды: ![]() и характерный временной масштаб ее нарастания:
и характерный временной масштаб ее нарастания: ![]() . Очевидно, что для нахождения этих масштабов нужно оценить коэффициент
. Очевидно, что для нахождения этих масштабов нужно оценить коэффициент ![]() . Из теории динамо [10-16] известно определение гидродинамической спиральности
. Из теории динамо [10-16] известно определение гидродинамической спиральности ![]() , которую выразим через безразмерную амплитуду источника:
, которую выразим через безразмерную амплитуду источника:
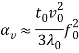
здесь ![]() – безразмерная амплитуда силы, входящая в формулу (50). При выводе этой формулы мы полагали установление баланса между источником и диссипацией в стационарном случае. Далее из формулы (50) коэффициент усиления
– безразмерная амплитуда силы, входящая в формулу (50). При выводе этой формулы мы полагали установление баланса между источником и диссипацией в стационарном случае. Далее из формулы (50) коэффициент усиления ![]() при малых числах параметра вращения
при малых числах параметра вращения ![]() (для центральной части нашей Галактики
(для центральной части нашей Галактики ![]() ) принимает вид:
) принимает вид:
![]()
Для оценок часто полагают ![]() (см. например [6, 15]), и в итоге характерные пространственный и временной масштабы соответственно равны:
(см. например [6, 15]), и в итоге характерные пространственный и временной масштабы соответственно равны:
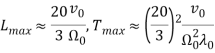
Используя эспериментальные данные для нашей Галактики: ![]() (центральная часть Галактики),
(центральная часть Галактики), ![]() ,
, ![]() (
(![]() ),
), ![]() [6, 15] легко найти численные оценки
[6, 15] легко найти численные оценки ![]() и
и ![]() :
: ![]() ,
, ![]() . Это вполне приемлемые оценки характерных масштабов для галактической генерации крупномасштабной вихревой структуры спирального типа.
. Это вполне приемлемые оценки характерных масштабов для галактической генерации крупномасштабной вихревой структуры спирального типа.
Литература:
1. Петвиашвили В. И., Похотелов О. А. Уединенные вихри в плазме и атмосфере. М.: Энергоатомиздат.1989. 200 с.
2. Абурджания Г. Д. Самоорганизация нелинейных вихревых структур и вихревой турбулентности в диспергирующих средах. М.: КомКнига. 2006. 328 с.
3. Онищенко О. Г., Похотелов О. А., Астафьева Н. М. Генерация крупномасштабных вихрей и зональных ветров в атмосферах планет // УФН. 2008. Т. 178. Вып. 6. С. 605–615.
4. Шмерлин Б. Я., Калашник М. В. Конвективная неустойчивость Рэлея в присутствие фазовых переходов влаги. Формирование крупномасштабных вихрей и облачных структур. // УФН. 2013.Т. 183. Вып. 5. С. 497–510.
5. Тур А. В., Яновский В. В. Гидродинамические вихревые структуры. Харьков: Институт монокристаллов. 2012. 290 с.
6. Рольфс К. Лекции по теории волн плотности. М.: Мир. 1980. 208 с.
7. Фридман А. М., Хоперсков А. В. Физика галактических дисков. М.: ФИЗМАТЛИТ. 2011. 632 с.
8. Незлин М. В., Снежкин Е. Н. Вихри Россби и спиральные структуры: Астрофизика и физика плазмы в опытах на мелкой воде. М.: Наука. 1990. 240 с.
9. Моффат Г. Некоторые направления развития турбулентности. Соврем. гидродинамика. Успехи и проблемы. М.: Мир. 1984. С. 48–76.
10. Штеенбек М., Краузе Ф. Возникновение магнитных полей звезд и планет в результате турбулентного движения их веществ. // Магнитная гидродинамика.1967. № 3. С. 19–44.
11. Моффат Г. Возбуждение магнитного поля в проводящей среде. М.: Мир. 1980. 343 с.
12. Зельдович Я. Б., Рузмайкин А. А., Соколов Д. Д. Магнитные поля в астрофизике. Ижевск: Инст. комп. иссл. РХД. 2006. 384 с.
13. Паркер Ю. Беседы об электрических и магнитных полях в космосе. Ижевск: Инст. комп. иссл. РХД. 2010. 208 с.
14. Краузе Ф., Рэдлер К.-Х. Магнитная гидродинамика средних полей и теория динамо. М.: Мир. 1984. 314 с.
15. Рузмайкин А. А., Соколов Д. Д., Шукуров А. М. Магнитные поля галактик. М.: Наука.1988. 279 с.
16. Соколов Д. Д., Степанов Р. А., Фрик П. Г. Динамо на пути от астрофизических моделей к лабораторному эксперименту. // УФН. 2014. Т.184. С. 318–335.
17. Krause F., Rudiger G. On the Reynolds stresses in mean-field hydrodynamics. I. Incompressible homogeneous isotropic turbulence. // Astron. Nachr.1974. V. 295. P.93–99.
18. Моисеев С. С., Сагдеев Р. З., Тур А. В., Хоменко Г. А., Яновский В. В. Теория возникновения крупномасштабных структур в гидродинамической турбулентности. // ЖЭТФ. 1983. Т. 85. С. 1979–1987.
19. Петросян А. С. Дополнительные главы теории турбулентности. Спиральная турбулентность. Москва: ИКИ РАН. 2013. 60 с.
20. Moiseev S. S., Rutkevitch P. B., Tur A. V., Yanovsky V. V. Vortex dynamos in a helical turbulent convection. // Sov. Phys. JETP.1988. Т. 67. С. 294–303.
21. Smith L. M. and Waleffe F. Transfer of Energy to Two-Dimensional Large Scales in Forced, Rotating Three-Dimensional Turbulence. // Physics of Fluids. 1999. V. 11. №. 6. – P. 1608.
22. Smith L. M. and Waleffe F. Generation of Slow Large Scales in Forced Rotating Stratified Turbulence. // Journal of Fluid Mechanics. 2002. V.451. P. 145–168.
23. Berezin Y. A. and Zhukov V. P. An Influence of Rotation on Convective Stability of Large Scale Distorbances in Turbulent Fluid. // Izv. AN SSSR. Mech. Zhidk. Gaza. 1989. V. 4. P. 3
24. Kitchatinov L. L., Rudiger G. and Khomenko G. Large-scale vortices in rotating stratified disks. // Astron. Astrophys.1994. V. 287. P. 320.
25. Rutkevich P. B. Equation for vortex Instability Caused by Convective Turbulence and Coriolis Force. // JETF. 1993. V. 77. P.933–938.
26. Kopp M., Tur A., Yanovsky V. The Large Scale Instability in Rotating Fluid with Small Scale Force // Open Journal of Fluid Dynamics. 2015. V. 5. P. 128–138.
27. Kopp M., Tur A., Yanovsky V. Nonlinear Vortex Structures in Obliquely Rotating Fluid. // Open Journal of Fluid Dynamics. 2015. V. 5. P. 311–321.
28. Копп М. И. Крупномасштабное магнитовращательное динамо. I. Линейная теория без внешнего магнитного поля // Альманах современной науки и образования. 2016. № 4 (106). С. 59–73.
29. Новиков Е. А. Функционалы и метод случайных сил в теории турбулентности. // ЖЭТФ. 1964. Т. 47. Вып.5(11). С. 1919–1926.
30. Кляцкин В. И. Стохастические уравнения и волны в случайно-неоднородных средах. М., Наука. 1980. 337 с.
31. Frishe U., She Z. S., Sulem P. L. Large Scale Flow Driven by the Anisotropic Kinetic Alpha Effect. // Physica D. 1987. V. 28. P. 382.
32. Дружинин О. А., Хоменко Г. А. Нелинейная теория гидродинамического альфа-эффекта в сжимаемой среде и обратный каскад энергии. В тр. Межд. конф.: Нелинейные и турбулентные процессы в физике. Киев: Наук. думка. 1989. Т. 2. С.83–86.
33. Rutkevitch P. B., Sagdeev R. Z., Tur A. V., Yanovsky V. V. Nonlinear dynamic theory of the ![]() -effect in compressible fluid. Proceeding of the IV Intern. Workshop on Nonlinear and Turb. Pros.in Physics. Kiev. 1989. V.2. P. 172–175.
-effect in compressible fluid. Proceeding of the IV Intern. Workshop on Nonlinear and Turb. Pros.in Physics. Kiev. 1989. V.2. P. 172–175.
34. Tur A. V., Yanovsky V. V. Large-scale instability in hydrodynamics with stable temperature stratification driven by small-scale helical force. — ArXiv: 1204.5024 v.1 [physics. Flu-dyn.](2012).
35. Tur A. V., Yanovsky V. V. Non Linear Vortex Structure in Stratified Driven by Small- scale Helical Forse. // Open Journal of Fluid Dynamics. 2013. V. 3. P. 64–74.
36. Чхетиани О. Г. Самоорганизация и турбулентность в отражательно-несимметричных плазменно-гидродинамических средах. Дисс. на соиск. уч. степени докт. физ.-мат. наук. Москва. 1999. 262 с.
37. Rudiger G. On the ![]() -Effect for Slow and Fast Rotation. // Astron. Nachr. 1978. V.299. №.4. P. 217–222.
-Effect for Slow and Fast Rotation. // Astron. Nachr. 1978. V.299. №.4. P. 217–222.







