Применение третьей теории прочности и сопротивления недренированному сдвигу для расчета безопасных давлений на земляное полотно

Применение третьей теории прочности исопротивления недренированному сдвигу для расчета безопасных давлений на земляное полотно

Батырова Вера Владимировна, студент

Сибирская государственная автомобильно-дорожная академия

В статье рассмотрена взаимосвязь сопротивления недренированному сдвигу с другими параметрами прочности и деформируемости грунтов. На основе третьей теории прочности получено решение для расчета безопасного давления.

Ключевые слова: земляное полотно, грунт, сопротивление недренированному сдвигу

Сопротивление недренированному сдвигу или как еще говорят недренированная прочность лежит в основе третьей теории прочности, адаптированной к грунтам. Согласно этой теории предельное состояние грунта описывается уравнением:

(1)

Где ₁ и ₃ — максимальное и минимальное главные напряжения, МПа; c_u

Известно, что третью теорию прочности можно записать в виде двухстороннего критерия [1, 2]. Если принять растяжение со знаком «минус», то этот критерий будет иметь вид:

Где R_p и R_c — пределы прочности на растяжение и сжатие, МПа.

Из совместного решения (1) и (2) вытекает:

(3)

В работах [3–5] приводятся эмпирические формулы, согласно которым сопротивление недренированному сдвигу связано с калифорнийским числом несущей способности грунта CBR линейной зависимостью. Эти формулы имеют вид:

(4)

Где a — параметр модели.

Также установлено, что калифорнийское число несущей способности связано с модулем упругости грунта. Такие эмпирические зависимости приведены в табл. 1.

Из анализа данных табл. 1 следует, что в общем виде CBR можно определить по формулам:

; (5)

Где b, c и d — параметры модели.

Эмпирические формулы для определения модуля упругости

Подстановка зависимостей (5) в выражение (4) приводит к формулам:

; (6)

В работах [9–12] представлено решение задачи о величине безопасных давлений на грунты земляного полотна. Согласно этому решению для вывода формулы безопасных давлений можно использовать метод линейно деформируемого полупространства. Согласно этому методу необходимо: обосновать условие пластичности, подставить в уравнение предельного равновесия принятого условия пластичности формулы для расчета главных напряжений и решить, полученное уравнение относительно давления. В качестве условия пластичности обычно принимают критерий Кулона-Мора, но в работах [13–17] показаны основные недостатки этого критерия и предприняты попытки замены его на более жесткое условие пластичности, в котором касательные напряжения имеют более высокие значения по сравнению с критерием Кулона-Мора. Анализ материалов публикации [13] показывает, что самым жестким критерием с наибольшими касательными напряжениями является третья теория прочности, по которой предельное состояние описывается уравнением (1). В этом уравнении можно использовать традиционные формулы механики сплошной среды [18, 19], позволяющие рассчитывать главные напряжения в любой точке сечения, расположенного на оси симметрии нагрузки. Однако в работах [20, 21] показаны недостатки этого решения и разработан способ расчета минимального главного напряжения, который позволяет модифицировать модели механики зернистой среды и инженерные способы расчета напряжений [22–25]. Согласно этому способу минимальное главное напряжение вычисляют по формуле

(7)

Формула для определения представляет собой функцию глубины и имеет вид:

(8)

где К — коэффициент затухания (уменьшения) вертикального напряжения от равномерной нагрузки под осью ее симметрии.

Представив максимальное главное напряжение произведением давления, передаваемого дорожной одеждой на земляное полотно и коэффициентом его затухания по глубине, являющимся функцией, получим формулу:

(9)

(10)

Решив зависимость (10) относительно давления получим:

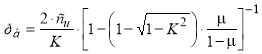(11)

Зависимость (11) позволяет рассчитывать безопасное давление, при котором в наиболее опасной точке земляного полотна наступает предельное состояние по третьей теории прочности. Величина безопасного давления, вычисленная по формуле (11) меньше, чем по другим формулам, но и этот самый жесткий расчет не гарантирует отсутствие эффекта накапливания остаточных деформаций грунтами земляного полотна. Поэтому наряду с расчетом по сопротивлению сдвигу, а именно по безопасным давлениям целесообразно выполнять расчет пластических деформаций [26–31] и сравнивать их с предельными глубинами неровностей [32–34]. Кроме того, полезно выполнять расчет по сопротивлению сдвигу асфальтобетонного покрытия, для которого можно задействовать методики, предложенные в работах [35, 36].

Литература:

1. Александров А. С. Совершенствование расчета дорожных конструкций по сопротивлению сдвигу. Том Часть 1. Состояние вопроса. — Омск: СибАДИ, 2015. — 292 с.
2. Гольденблат И. И., Копнов В. А. Критерии прочности и пластичности конструкционных материалов. — М.: Машиностроение, 1968. — 192 с.
3. Семенова Т. В., Долгих Г. В., Полугородник Б. Н. Применение Калифорнийского числа несущей способности и динамического конусного пенетрометра для оценки качества уплотнения грунта // Вестник СибАДИ, 2014, № 1 — С. 59–66.
4. Александрова Н. П., Троценко Н. А. Применение измерителя жесткости грунта Geogauge для оценки качества уплотнения при операционном контроле // Вестник СибАДИ, 2014, № 3 — С. 40–47.
5. Александрова Н. П., Семенова Т. В., Стригун К. Ю. Совершенствование методов экспресс оценки качества уплотнения грунтов земляного полотна строительства автомобильных дорог / Н. П. Александрова, // Вестник СибАДИ. — 2015. — № 4. — С. 46–57.
6. Heukelom W., Klomp A. J. G. Dynamic Testing as a Means of Controlling Pavements During and After Construction. Proc., of 1st International Conference on Structural Design of Asphalt Pavements. 1962.
7. Witczak M. W., Qi X., Mirza M. W. Use of Nonlinear Subgrade Modulus in AASHTO Design Procedure // Journal of Transportation Engineering, Vol. 121, No. 3 1995. Pp. 273–282.
8. Puppala A. J. Estimating Stiffness of Subgrade and Unbound Materials for Pavement Design // NCHRP Synthesis 382, Transportation Research Board, National Research Council, Washington, DC 2008. 139 p.
9. Александров А. С., Долгих Г. В., Калинин А. Л. О допускаемых давлениях на грунты земляного полотна и слои дорожной одежды // Наука и техника в дорожной отрасли. — 2012. № 2. — С. 10–13.
10. Александров А. С. Совершенствование расчета дорожных конструкций по сопротивлению сдвигу. Том Часть 2. Предложения: монография. — Омск: СибАДИ, 2015. — 262 с.
11. Долгих Г. В. Расчет грунтов земляного полотна по критерию безопасных давлений // Вестник Сибирской государственной автомобильно-дорожной академии. — 2013. — № 6 (34). — С. 43–49.
12. Долгих Г. В. Расчет нежестких дорожных одежд по критерию безопасных давлений на глинистые грунты земляного полотна // Автореф. Дис. канд. техн. наук. — Омск: СибАДИ. — 2014. — 20 с.
13. Александров А. С., Калинин А. Л. Совершенствование расчета дорожных конструкций по сопротивлению сдвигу. Часть 1. Учет деформаций в условии пластичности Кулона-Мора // Инженерно-строительный журнал. — 2015. № 7 (59). — С. 4–17.
14. Александрова Н. П., Александров А. С., Чусов В. В. Модификация критериев прочности и условий пластичности при расчетах дорожных одежд // Вестник Сибирской государственной автомобильно-дорожной академии. — 2015. № 1 (41). — С. 47–54.
15. Чусов В. В. Перспективы применения эмпирических условий пластичности грунтов и определение их параметров при трехосных испытаниях грунтов Вестник ВолГАСУ. — 2015. № 4 (61). — С. 49–57.
16. Александров А. С., Долгих Г. В. Калинин А. Л. Модификация критериев прочности сплошной среды для расчета грунтов земляного полотна по сопротивлению сдвигу // В сборнике: Архитектура. Строительство. Транспорт. Технологии. Инновации Материалы Международного конгресса ФГБОУ ВПО «СибАДИ». — Омск: СибАДИ, 2013. — С. 228–235.
17. Александров А. С., Долгих Г. В., Калинин А. Л. Применение критерия Друкера-Прагера для модификации условий пластичности // Наука и техника в дорожной отрасли. — 2013. № 2. — С. 26–29.
18. Foster, С.R., Ahlvin R. G. Stresses and deflections induced by a uniform circular load. // Proc. Highway Research Board. — 1954. — Vol. 33. — P. 236–246.
19. Craig R. F. Soil Mechanics. — Seventh edition. Department of Civil Engineering, University of Dundee, UK. — Published by Taylor & Francis e-Library, London and New York, 2004. — 447 p.
20. Александров А. С., Долгих Г. В., Юрьев Д. В. Расчет главных напряжений в слоях дорожной одежды из дискретных материалов // Транспортное строительство. — 2011. — № 7. — С. 17–22.
21. Александров А. С. Один из путей расчета минимальных главных напряжений в грунтах земляного полотна // В сборнике: Архитектура. Строительство. Транспорт. Технологии. Инновации Материалы Международного конгресса ФГБОУ ВПО «СибАДИ». — Омск, СибАДИ, 2013. — С. 217–228.
22. Александрова Н. П., Семенова Т. В., Долгих Г. В. Совершенствование моделей расчета главных напряжений и девиатора в грунте земляного полотна // Вестник СИБАДИ. — 2014. — № 2 (36). С. 49–54.
23. Александрова Н. П. Модифицированные модели для расчета главных напряжений в грунте земляного полотна // В сборнике: Архитектура. Строительство. Транспорт. Технологии. Инновации Материалы Международного конгресса ФГБОУ ВПО «СибАДИ». Омск, 2013. — С. 236–246.
24. Александров А. С., Долгих Г. В. Калинин А. Л. Один из путей совершенствования расчета дорожных одежд по условию сопротивления сдвигу в грунте земляного полотна // Модернизация и научные исследования в транспортном комплексе. — Пермь: Пермский национальный исследовательский политехнический университет, 2013. — С. 9–22.
25. Александров А. С., Александрова Н. П., Долгих Г. В. Модифицированные модели для расчета главных напряжений в дорожных конструкциях из дискретных материалов // Строительные материалы. — 2012. — № 10. — С. 14–17.
26. Семенова Т. В., Гордеева С. А., Герцог В. Н. Определение пластических деформаций материалов, используемых в дорожных конструкциях // Вестник Томского государственного архитектурно-строительного университета. — 2012. — № 4 (37). — С. 247–254.
27. Семенова Т. В., Герцог В. Н. Пластическое деформирование материалов с дискретной структурой в условиях трехосного сжатия при воздействии циклических нагрузок // Вестник Сибирской государственной автомобильно-дорожной академии. — 2013. — № 1 (29). — С. 68–73.
28. Александров А. С., Киселева Н. Ю. Пластическое деформирование гнейс- и диабаз материалов при воздействии повторяющихся нагрузок // Известия высших учебных заведений. Строительство. — 2012. — № 6. — С. 49–59.
29. Александров А. С. Пластическое деформирование гранодиоритового щебня и песчано-гравийной смеси при воздействии трехосной циклической нагрузки // Инженерно-строительный журнал. — 2013. — № 4 (39) — С. 22–34.
30. Александров А. С. Применение теории наследственной ползучести к расчету деформаций при воздействии повторных нагрузок: монография. — Омск: СибАДИ, 2014. — 152 с.
31. Александров А. С. Обобщающая модель пластического деформирования дискретных материалов дорожных конструкций при воздействии циклических нагрузок // Строительные материалы. 2016. № 5. С. 27–30.
32. Герцог В. Н., Долгих Г. В., Кузин В. Н. Расчет дорожных одежд по критериям ровности. Часть 1. Обоснование норм ровности асфальтобетонных покрытий // Инженерно-строительный журнал. — 2015. — № 5 (57) — С. 45–57.
33. Александров А. С., Гордеева С. А., Шпилько Д. Н. О допускаемых и предельных значениях неровностей асфальтобетонных покрытий дорожных одежд жесткого типа //Автомобильная промышленность. — 2011. — № 2. — С. 31–35.
34. Александров А. С., Александрова Н. П., Семенова Т. В. О проектировании шероховатости дорожных покрытий и дождевой канализации по условиям безопасности движения // Автомобильная промышленность. — 2008. — № 8 — С. 36–38.
35. Чусов В. В. Применение теории накапливания повреждений в условиях пластичности асфальтобетона для расчета дорожных покрытий по сопротивлению сдвигу // Молодой ученый. — 2016. — № 6 (110). — С. 221–227.
36. Александрова Н. П., Александров А. С., Чусов В. В. Учет поврежденности структуры асфальтобетона в критериях прочности и условиях пластичности // В сборнике: Политранспортные системы материалы VIII Международной научно-технической конференции в рамках года науки Россия — ЕС. Новосибирск: СГУПС, 2015. — С. 219–225.