Хаотические процессы изучаются довольно давно и интенсивно, однако, их изучение требует именно моделирования. А моделирование требует зачастую дорогих программных продуктов. Но для исследований можно использовать и свободно распространяемые программы. Одну такую программу мы и рассмотрим — Blender. С ее помощью мы попытаемся исследовать хаотический маятник.
Для начала определимся с понятиями.
Чтобы понять, что такое хаотические процессы нужно сначала сказать, что такое аттрактор — это множество точек в фазовом пространстве диссипативной системы, посещаемых в установившемся режиме. Простой пример — устойчивое состояние равновесия и предельный цикл, отвечающий режиму периодических автоколебаний. Хаотические процессы же характеризуются тем, что сколь угодно малая неточность в задании начальных условий быстро нарастает во времени. И имеет странные аттракторы — сложно устроенные множества, демонстрирующие все более тонкую структуру на разных уровнях ее разрешения (фракталы). [1]
Двойной маятник — по сути это мятник на свободном конце другого маятника. Поведение такой системы намного сложнее, нежели у простого, либо у физического мятников.
В режиме малых колебаний у двойного маятника возникает такое явление какэффект биений. А при увеличении энергии характер колебаний маятников меняется принципиально − колебания становятсяхаотическими. Несмотря на то, что двойной маятник можно описать системой нескольких обыкновенных дифференциальных уравнений, то есть вполне детерминированной моделью, появление хаоса выглядит очень необычно. Данная ситуация напоминает систему Лоренца, где детерминированная модель из трех уравнений также демонстрирует хаотическое поведение. Стоит увеличить углы и двойной маятник сможет демонстрировать хаотическое движение, которое чувствительно к начальным условиям. [2]
Blender 3D — свободно распространяемый программный комплекс для 3D моделирования, с встроенным игровым движком, управляемым языком программирования Python 3.5. [3]
Математическая модель маятника.
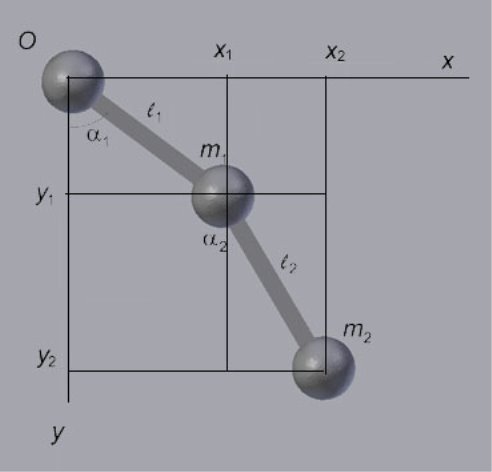
Рис 1. 1 — математический двойной маятник
Введем систему координат Oxy, начало которой совпадает с точкой подвеса. Координаты маятников определяются следующими соотношениями:
Кинетическая и потенциальная энергия маятников (соответственно T и V) выражаются формулами
![]() (2)
(2)
Тогда лагранжиан записывается в виде
![]() (3)
(3)
Учтем, что
![]()
![]() (4)
(4)
Следовательно,
![]()
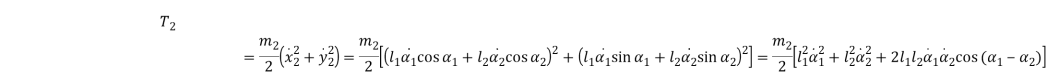 (5)
(5)
![]() (6)
(6)
В результате лагранжиан системы принимает такой вид:
 (7)
(7)
Теперь мы можем составить уравнения Лагранжа (иногда их называют уравнениями Эйлера-Лагранжа):
![]()
Входящие в уравнения частные производные выражаются следующими формулами:
![]()
![]() (8)
(8)
![]()
![]() (9)
(9)
Следовательно, первое уравнение Лагранжа записывается как
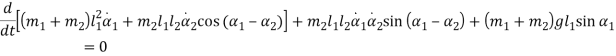
![]()
![]()
![]()
Сокращая на ![]() , получаем:
, получаем:
![]() (10)
(10)
Аналогично выведем второе дифференциальное уравнение:
![]()
![]()
![]()
После сокращения на ![]() уравнение принимает такой вид:
уравнение принимает такой вид:
![]()
Таким образом, нелинейная система двух дифференциальных уравнений Лагранжа записывается как
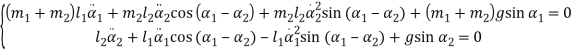 (12)
(12)
Эту математическую модель и применим для моделирования.
Программа в Python 3.5
Для применения описанной выше математической модели составим программу на Python
Листинг:
import math #Импорт модуля математических команд
add1=0; ad1=0; a1=4; add2=0; ad2=0; a2=4; x1=0; x2=0; y1=0; y2=0;
m1=10; m2=15; l1=5; l2=6; g=9.8;
dt=0.001; i=0 #Начальные условия
while i<15:
add1=(m2*l2*add2*math.cos(a1-a2)+m2*l2*ad2*ad2*math.sin(a1-a2)+(m1+m2)*g*math.sin(a1))/(-(m1+m2)*l1)
add2=(l1*add1*math.cos(a1-a2)-l1*ad1*ad1*math.sin(a1-a2)+g*math.sin(a2))/(-l2)
#программная реализация формулы (12)
ad1=ad1+add1*dt
a1=a1+ad1*dt
ad2=ad2+add2*dt
a2=a2+ad2*dt
x1=l1*math.sin(a1)
x2=l1*math.sin(a1)+l2*math.sin(a2)
y1=-l1*math.cos(a1)
y2=-l1*math.cos(a1)-l2*math.cos(a2)
# перевод из полярной в декартову систему координат.
i=i+dt
print (a1, a2)
Результат работы программы — это углы наклона первого и второго маятников.
Моделирование в Blender 3D
Теперь модифицируем описанную выше программу под среду Blender
Листинг:
import bge #Импорт модуля Bleder Game Engine
import math #Импорт модуля математических команд
object = bge.logic.getCurrentController().owner
add1=object['add1']; ad1=object['ad1']; a1=object['a1']; add2=object['add2']; ad2=object['ad2']; a2=object['a2']; x1=object['x1']; x2=object['x2']; y1=object['y1']; y2=object['y2'];
m1=object['m1']; m2=object['m2']; l1=object['l1']; l2=object['l2']; g=object['g'];
dt=object['dt']; i=object['i']
object['add1']=((m2*l2*object['add2']*math.cos(object['a1']-object['a2'])+m2*l2*object['ad2']*object['ad2']*math.sin(object['a1']-object['a2'])+(m1+m2)*g*math.sin(object['a1']))/(-(m1+m2)*l1))-(object['a1'])*0.3
object['add2']=(l1*object['add1']*math.cos(object['a1']-object['a2'])-l1*object['a1']*object['a1']*math.sin(object['a1']-object['a2'])+g*math.sin(object['a2']))/(-l2)
object['ad1']=object['ad1']+object['add1']*dt
object['a1']=object['a1']+object['ad1']*dt
object['ad2']=object['ad2']+object['add2']*dt
object['a2']=object['a2']+object['ad2']*dt
object['x1']=l1*math.sin(object['a1'])
object['x2']=l1*math.sin(object['a1'])+l2*math.sin(object['a2'])
object['y1']=-l1*math.cos(object['a1'])
object['y2']=-l1*math.cos(object['a1'])-l2*math.cos(object['a2'])
object['i']=object['i']+object['dt']
object.applyRotation ([0,0,object['ad1']]) #Задание скорости объекта

Рис. 2. окно программирования в Blender

a)

б)
Рис 3. а, б —визуализация траектории
Код применяется отдельно к каждому плечу модели. Отличаясь последней строчкой задающей скорость.
Таким образом, мы визуализировали с помощью Blender математическую модель, представленную выведенными формулами. Но что если нам неизвестна математическая модель? Можно воспользоваться физической симуляцией в Blender.
Физическая симуляция
На следующем рисунке представлена модель, которая работает на встроенной в Blender физике. Верхнее звено жестко закреплено в пространстве, остальные при стимуляции ведут себя согласно законам физики.

Рис. 4. 3D-модель хаотического маятника с физикой в Blender
Выводы.
- Получена модель с визуализацией по математическому описанию с использованием свободного программного обеспечения.
- Получена модель хаотического маятника с использованием физической симуляции Blender.
- Даиные методы моделирования позволяют сократить затраты на пакеты моделирования и обладают большими потенциальными возможностями, так как моделирование можно проводить с объектами любой формы с использованием любого кода.
Литература:
- Кузнецов С. П. Динамический хаос. — ФИЗМАТЛИТ, 2006. 356 с. ISBN 5–94052–100–2
- Заславский Г. М., Сагдеев Р. З. Введение в нелинейную физику: от маятника до турбулентности и хаоса. -Главная редакция физико-математической литературы издательства «Наука». 368 с. ISBN5–02–013822–3
- Прахов А.А Blender: 3D-моделирование и анимация. Руководство для начинающих БХВ-Петербург 2012. 272 с. ISBN:978–5-9775–0393–8







