In [1] the notion of a quadratic stochastic operator was introduced. Such operators arise in problems of mathematical biology and mathematical genetics [1–7]. Let
be the 
-dimensional simplex.
A map 
from 
into itself is called a quadratic stochastic operator (shortly QSO) if
(1)
for any 
, where
(2)
Assume that 
is the trajectory of the initial point 
,where 
for all 
, with 
.
A point 
is called a fixed point of a QSO 
if 
.
A QSO 
is called regular if for any initial point 
, the limit 
exists. Note that the limit point is a fixed point of a QSO. Thus, the fixed points of a QSO describe limit or long run behavior of the trajectories for any initial point.
In [7], Zakharevich proved that this conjecture is false in general. The biological treatment of non-ergodicity of a QSO is the following: in a long run the behavior of the distributions of species is chaotic, i.e. it is unpredictable. Note that a regular QSO is ergodic, but in general from ergodicity does not follow regularity.
Let the set 
be the interior of 
and 
be the set of limit points of the trajectory 
.
A quadratic stochastic operator is called Volterra if 
for any 
.
The biological treatment of such operators is rather clear: the offspring repeats one of its parents. Recall the definition of quasi-Volterra operator following [2].
Definition [2]. A quadratic stochastic operator (1), (2) is said to be a quasi-Volterra operator if only one coefficient 
is non-zero when 
and all others are zero.
All quasi-Volterra QSOs defined on two-dimensional simplex can be divided into two types.
Without lost of generality we may assume 
then an arbitrary quasi-Volterra operator of first type has the following representation:
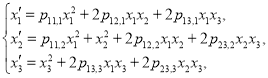(3)
Similarly without lost of generality we may assume 
then an arbitrary quasi-Volterra operator of second type has the following representation:
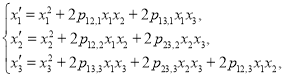(4)
In [2] the sets of fixed points of the quasi-Volterra operators (3) and (4) are described and for some special classes of first and second type quasi-Volterra operators it was proven that ergodic hypotheses true.
Let us consider the following quasi-Volterra quadratic stochastic operator
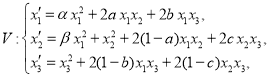(5)
where 
and 
.
In general, the main problem of the study of the asymptotic behavior of a quasi-Volterra QSO is also a difficult problem, which remains open, even in the two-dimensional simplex case. Below we consider the case 
.
It is easy to check that i) the quasi-Volterra QSO (5) is first type and ii) the quasi-Volterra QSO (5) doesn't coincide with quasi-Volterra QSOs which were studied in [2].
Theorem: Let .
i) If 
then for any initial point the trajectory of quasi-Volterra QSO (5) converges to vertex 
;
ii) If 
then for any initial point the trajectory of quasi-Volterra QSO (5) converges to vertex 
;
iii) If 
then 
for any initial point 
.
Corollary: Assume conditions of items i), ii) of Theorem are satisfied, then a quasi-Volterra QSO (5) is regular operator and it is an ergodic transformation.
References:
- Bernstein, S.N.: Solution of a mathematical problem connected with the theory of heredity. Ann. Math. Statistics 13, 53–61 (1942).
- Ganikhodjaev, N.N., Mukhitdinov, R.T.: On a class of non-Volterra quadratic operators. Uzbek Math. J. 3–4, 9–12 (2003), (in Russian).
- Ganikhodzhaev, R.N.: Quadratic stochastic operators, Lyapunov functions and tournaments. Sb. Math. 76, 489–506 (1993).
- Ganikhodzhaev, R.N.: Map of fixed points and Lyapunov functions for one class of discrete dynamical systems. Math. Notes 56, 1125--1131 (1994)
- Ganikhodzhaev, R.N., Mukhamedov, F.M., Rozikov, U.A.: Quadratic stochastic operators and processes: results and open problems. Infin. Dimens. Anal. Quantum Probab. Relat. Top. 14, 279--335 (2011).
- Lyubich, Y.I.: Mathematical structures in population genetics. Volume 22 of Biomathematics. Springer-Verlag, Berlin (1992).
- Zakharevich, M.I.: On the behaviour of trajectories and the ergodic hypothesis for quadratic mappings of a simplex. Russ. Math. Surv. 33, 265--266 (1978).
