В работе рассматриваться линейные собственные колебания упругого криволинейного стержня.
In this work linear collaboration of an elastic wry stock is learned.
Задача о собственных колебаниях криволинейного стержня, контактирующего с вязкой жидкостью сводится к спектральной задаче по параметру 
для системы обыкновенных дифференциальных уравнений [1]
;
;
;
; (1)
;
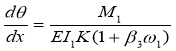где - плотность материала; M-крутящий момент относительно оси вращения; К — кривизна осевой линии; S — поперечное сечение.
Полагается, что при собственных колебаниях упругого стержня отсутствуют взаимодействия неупругого происхождения, включая трение, и движение подчиняется гармоническому закону
, (2)
где Y — вектор собственных форм; ω — частота колебаний. В этом случае
,
.
Колебания сплошного криволинейного стержня. Рассматривается стальной криволинейный стержень постоянного прямоугольного сечения и постоянной кривизны, один конец которого жёстко заделан, а другой свободен. Размер стержня (в мм): длина 210; поперечное сечение 3,2*18,2; радиус кривизны 57,8. Подлежат исследованию собственные изгибно-продольные колебания. И после некоторых преобразований (1) получим следующий синтез обыкновенных дифференциальных уравнений:
(3)
где К=1 для сложных стержней в силу условий закрепления на краях стержня справедливы соотношения
X = O; U = W = Q = O; X = L; T = Q1 = M1 = O. (4)
Необходимо найти также значения 
, при которых система уравнений с краевыми условиями (4). Последняя задача была решена численно методом ортогонального прогонки Годунова. Найденные для значений
Е = 19,6 * 104 МПа, p = 8 г/см3 первые три собственные частоты колебаний приведены в таблице вместе с результатами эксперимента.
|
Частота (Гц) |
|||
|
№частоты |
1 |
2 |
3 |
|
Расчёт |
75,3 |
212 |
713 |
|
Эксперимент |
75 |
204 |
680 |
Согласно таблице, отличие между экспериментальными и расчётными данными больше для высоких частот, но в целом не превышают 5 %.
Колебания тонкостенного криволинейного стержня. Исследуются собственные изгибно-родольные колебания стальной трубки Бурдона плоскоовального сечения, закреплённой также, как и стержень в примере I. Размеры трубки (в мм): длина 240; толщина стенки 0,2; большая и малая полуоси сечения 9,5 и 3,2; радиус кривизны 45,2. Модуль Юнга Е = 20,6 МПа; объёмная плотность p=78 г/ см3, коэффициент Пуассона γ = 0,25.
Постановка спектральной проблемы даётся соотношениями (3) и (4). Минимальная соответственная частота, полученная при решении краевой задачи методом ортогональной прогонки, составляет 88,6 Гц.
По данным эксперимента, первый резонанс трубки наблюдался на 100 Гц. Несколько заниженное расчётное значение частоты объясняется тем, что стержневая модель не учитывает реальных условий закрепления на концах трубки, вблизи которых эффект Кармана проявляется в меньшей степени.
Здесь, в отличие от упругого случая, собственная частота 
и собственная форма колебаний могут принимать комплексные значения. Действительная и мнимая части величины имеют физический смысл соответственно и частоты и скорости затухания колебательного процесса по времени. Логарифмический декремент затухания вычисляется по формуле:
.
Краевая задача (1) была решения численно методом ортогональной прогонки в комплексной арифметике. Численный анализ задачи о собственных колебаниях криволинейного стержня, контактирующего с вязкой жидкостью, позволил сделать следующие выводы.
С ростом собственного движения декременты затухания увеличиваются при наличии внутреннего трения и уменьшаются при внешнем трении. Причем, с увеличением интенсивности диссипации апериодические режимы (чисто мнимые собственные значения) возникают, начиная с наиболее высоких номеров собственных движений, в случае внутреннего трения, и с наиболее высоких номеров собственных движений в случае внешнего трения. Исключения из этого правила наблюдались только при неоднородном внешнем трении для сильно искривленных стержней (КL>3,14), у которых с ростом KL максимальный декремент затухания переходит с первого собственного движения на второе. В случае прямого стержня аналогичный эффект был впервые установлен Бидерманом.
При однородной диссипации собственные формы совпадают с соответствующими по номеру собственными формами упругих колебаний. Для колебательных режимов мнимые части собственных значений линейно зависят от параметра в случае внутреннего трения. В случае внешнего трения мнимая часть различных собственных значений одинаково не зависит от кривизны оси и определяется выражением
.
Если трение неоднородно, собственные формы зависят от интенсивности диссипации, причем колебания различных пространственных точек сдвинуты по фазе. Благодаря учету диссипации энергии, модель вязкоупругого стержня позволяет исследовать вынужденные установившиеся колебания при резонансах. Предположим, что стержень подвергается воздействию так, что его конец в месте закрепления совершает плоское движение по известному гармоническому закону
,
или с учетом замены (1)
. (5)
Тогда формы установившихся колебаний суть решения краевой задачи (1) и (5). В данном случае величина принимает известные действительные значения и имеет смысл круговой частоты вынуждающего воздействия.
Из физических соображений понятно, что при наличии диссипации однородная спектральная задача (1), (5) будет иметь ненулевые решения только для комплексных собственных значений . Это решение, как и решение задачи о собственных значениях, определялось с помощью программного аппарата методом ортогональной прогонки.
Литература:
1. Сафаров И. И. Колебания и волны в диссипативно неоднородных средах и конструкциях.// Ташкент: Фан, 1992, -C. 130.
2. Базаров М. Б., Сафаров И. И., Шокин Ю. И. «Численное моделирования колебаний диссипативно однородных и неоднородных механических систем».- Новосибирск: Изд.СО РАН.1996.-189 ст.
