Модифицированный динамический инженерный метод расчета главных напряжений в дискретных материалах дорожных конструкций



Модифицированный динамический инженерный метод расчета главных напряжений вдискретных материалах дорожных конструкций

Грязнова Марина Константиновна, студент

Сибирская государственная автомобильно-дорожная академия

В статье кратко описаны методики расчета главных напряжений в дорожных конструкциях. Объединены два метода «СибАДИ», что позволило рассчитывать минимальные главные напряжения в дискретных материалах через величину максимального главного напряжения от динамической нагрузки, изменяющейся во времени по синусоиде.

Ключевые слова: дорожная конструкция, главные напряжения динамическая нагрузка

В настоящее время разработан ряд методов, позволяющих рассчитывать характеристики напряженно-деформированного состояния (НДС) в дорожных конструкциях от динамических нагрузок, распределенных по круглой площадке. Эти методы условно разделим на точные [1–3], в основе которых использован смешанный метод теории упругости, и инженерные [4–6], позволяющие рассчитывать только одну вертикальную компоненту в тензорах напряжений и деформаций. Достоинство точных методов расчета, берущих свое начало в работах Д. Бурмистра [7, 8], К. Юшиты [9], Ю. Хуанга [10] и др. выдающихся ученых известных во всем мире состоит в том, что эти решения позволяют вычислять все компоненты тензора напряжений и деформаций. Такие решения удовлетворяют всем канонам механики сплошной среды, в частности линейной теории упругости, но конечные математические выражения громоздки и без вычислительного программного обеспечения сложно реализуются на практике. Инженерные методы [4–6] и подобные удовлетворяют только часть допущений и постулатов теории упругости и позволяют вычислять только вертикальное нормальное напряжение и вертикальную относительную деформацию, зато формулы для определения этих компонент тензоров просты и легко применяются специалистами при исчислении. В настоящей публикации автор предпримет попытку модификации инженерного метода расчета напряжений, предложенного в работе [6]

Согласно решению [4–6] вертикальное нормальное напряжение в слое можно определить по формуле, которую запишем в общем виде:

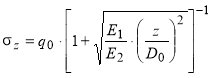(1)

Где q₀ — нагрузка, распределенная по круглой площадке, на поверхности рассчитываемого слоя, Па; E₁ и Е₂ — модули упругости материалов верхнего (рассчитываемого) и нижнего слоев, в случае если подстилающий слой является слоистым полупространством, то Е₂ может быть найден, как общий модуль упругости на поверхности подстилающего полупространства, Па; z — глубина расположения точки в рассчитываемом слое, определяемая расстоянием от поверхности слоя до этой точки, м; D₀ — диаметр круглой площадки, по которой распределена нагрузка на поверхности рассчитываемого слоя, м.

В сечении расположенном по оси симметрии нагрузки, распределенной по круглой площадке, направления главных и координатных осей совпадают, вследствие чего в этом сечении имеют место равенства ₁=_z, ₁=_x, ₁=_y [11]. Поэтому в сечении по оси симметрии нагрузки формулу (1) можно применить для расчета как вертикального нормального, так и максимального главного напряжения, но в слоях из дискретных материалов и грунтах земляного полотна. Для расчета минимальных главных напряжений применим способ, опубликованный в работах [12]. Этот способ применим для определения напряжений в полупространстве [13], а так же слое конечной толщины [14], что позволило модифицировать ряд моделей механики зернистой среды и инженерных способов расчета [15–17].

Следуя этим работам минимальное главное напряжение в полупространстве определяют по формулам:

; (2)

где  — функция глубины;  — коэффициент Пуассона;  — коэффициент бокового давления; К — коэффициент уменьшения максимального главного напряжения по глубине в сечении по оси симметрии нагрузки.

Из анализа зависимости (1) следует, что коэффициент К определяется вторым множителем, заключенным в квадратные скобки, то есть

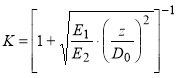(3)

Зависимость (3) применима к полупространству. В соответствии с данными работы [14] для расчета К в слое конечной толщину нужно применить метод Н. Одемарка:

В методе Н. Одемарка [18] имеется возможность рассчитать приведённую по жесткости ординату точки в полупространстве z к ординате точки в слое конечной толщины z_сл. Сделать это можно по формуле:

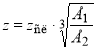(4)

где z_сл — ордината точки, расположенной на оси симметрии нагрузки слоя толщиной h, то есть 0z_слh, м; E_сл — модуль упругости материала слоя, МПа; E_осн — общий модуль упругости на поверхности однородного или слоистого полупространства, подстилающего рассчитываемый слой, МПа.

Тогда с учетом (4) зависимость (3) примет вид:

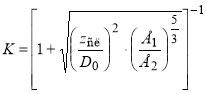(5)

Подставляя выражение (5) во вторую формулу зависимостей (2), получим:

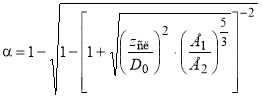(6)

Подставив зависимости (1) и (6) в первое выражение формул (2), получим:

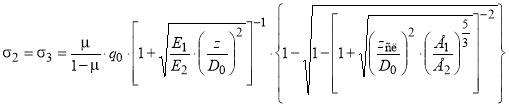(7)

Предложенная автором модель, включающая в себя известную и новую формулы (1) и (7), является новой модификацией, полученной применением способа [12–14]. Этой модели в работах [15–17] нет, поэтому она дополняет перечень модифицированных моделей для расчета главных напряжений в дискретных средах в сечении по оси симметрии нагрузки. Область ее применения достаточно широка, можно использовать при вычислении допускаемых давлений на земляное полотно и слои дорожной одежды [19–23], или при расчете необратимых деформаций в материалах с дискретной структурой [24–26]. При допущении, что при достаточно высоких температурах асфальтобетона в сравнительно толстых слоя, возникает трехосное сжатие, то эта модель применима для: расчета деформаций [27, 28], эквивалентных напряжений в критериях прочности [29–31], мер теории накапливания повреждений [31–34].

Литература:

1. Колмогоров Г. Л., Кычкин В. И., Есипенко И. А. Метод конечных разностей в исследовании дорожных одежд при воздействии реальной транспортной нагрузки // Строительная механика инженерных конструкций и сооружений. — 2014. — № 1. — С. 69–77.

2. Колмогоров Г. Л., Кычкин В. И., Есипенко И. А. Динамическая реакция дорожной одежды на действие динамической нагрузки // Строительная механика инженерных конструкций и сооружений. — 2015. — № 5. — С. 39–47.

3. Есипенко И. А., Колмогоров Г. Л., Кычкин В. И. Численное моделирование колебаний дорожной одежды с учетом изменения приведенных физико-механических свойств материала // Транспорт. Транспортные сооружения. Экология. — 2014. — № 3. — С. 57–73.

4. Смирнов А. В., Андреева Е. В. Динамическое напряженное состояние слоев дорожных одежд конструкций, изгибаемых колебательным волновым полем // Вестник Сибирской государственной автомобильно-дорожной академии. — 2012. — № 5 (27) — С. 68–70.

5. Смирнов А. В., Андреева Е. В., Герцог В. Н. Воздействие подвижных нагрузок на покрытия и основания автомагистралей // В сборнике: Актуальные проблемы архитектуры и строительства Материалы международной научно-практической конференции. 2014. С. 117–124.

6. Смирнов А. В., Андреева Е. В., Игнатов В. Ф. Динамические процессы в дорожных конструкциях // Вестник Сибирской государственной автомобильно-дорожной академии. — 2015. — № 5 — С. 81–86.

7. Burmister D. M. The Theory of Stresses and Displacements in Layered Systems and Applications to the Design of Airport Runways // Proceedings, Highway Research Board. — 1943. –Vol. 23. — P. 126–144.

8. Burmister, D. M. Stress and Displacement Characteristics of a Two-Layered Rigid Base Soil System: Influence Diagrams and Practical Applications. // Proceedings Highway Research Board. — 1956. — Vol. 35. — P. 773–814.

9. Ueshita K., Meyerhof, G. G. Surface Displacement of an Elastic Layer under Uniformly Distributed Loads // Highway Reasearch Board Record. — 1968. — №. 228. — P. 1–10.

10. Huang Y. H. Computation of Equivalent Single-wheel Loads Using Layered Theory // Proceedings, Highway Research Board. 1969.

11. Александров А. С. Применение теории наследственной ползучести к расчету деформаций при воздействии повторных нагрузок: монография. — Омск: СибАДИ, 2014. — 152 с.

12. Александров А. С., Долгих Г. В., Юрьев Д. В. Расчет главных напряжений в слоях дорожной одежды из дискретных материалов // Транспортное строительство. — 2011. — № 7. — С. 17–22.

13. Александров А. С., Долгих Г. В. Способ определения минимального главного напряжения. Часть 1. В грунтах земляного полотна. // В сборнике: Наука XXI века: опыт прошлого — взгляд в будущее: материала II международной научно-практической конференции — Омск, СибАДИ, 2016 — С. 64–68.

14. Александров А. С., Долгих Г. В. Способ определения минимального главного напряжения. Часть 2. В слоях дорожной одежды из дискретных материалов // В сборнике: Наука XXI века: опыт прошлого — взгляд в будущее: материала II международной научно-практической конференции — Омск, СибАДИ, 2016. — С. 69–73.

15. Александрова Н. П. Модифицированные модели для расчета главных напряжений в грунте земляного полотна // В сборнике: Архитектура. Строительство. Транспорт. Технологии. Инновации Материалы Международного конгресса ФГБОУ ВПО «СибАДИ». Омск, 2013. — С. 236–246.

16. Александрова Н. П., Семенова Т. В., Долгих Г. В. Совершенствование моделей расчета главных напряжений и девиатора в грунте земляного полотна // Вестник СИБАДИ. — 2014. — № 2 (36). С. 49–54.

17. Александров А. С., Александрова Н. П., Долгих Г. В. Модифицированные модели для расчета главных напряжений в дорожных конструкциях из дискретных материалов // Строительные материалы. — 2012. — № 10. — С. 14–17.

18. Odemark N. Investigations as to the Elastic Properties of Soils and Design of Pavements according to the Theory of Elasticity. Ph.D. thesis. Statens Väginstitut, Mitteilung No. 77. Stockholm, Sweden, 1949.

19. Александров А. С., Долгих Г. В., Калинин А. Л. О допускаемых давлениях на грунты земляного полотна и слои дорожной одежды // Наука и техника в дорожной отрасли. — 2012. № 2. — С. 10–13.

20. Долгих Г. В. Применение безопасного давления в качестве критерия расчета земляного полотна по сдвигу в грунте // В сборнике: Наука XXI века: опыт прошлого — взгляд в будущее: материала II международной научно-практической конференции — Омск, СибАДИ, 2016. — С. 113–117.

21. Долгих Г. В. Применение критерия безопасных давлений для расчета дорожных конструкций по сопротивлению сдвигу в грунте земляного полотна // В сборнике: Политранспортные системы материалы VIII Международной научно-технической конференции в рамках года науки Россия — ЕС. Новосибирск: СГУПС, 2015. — С. 176–182.

22. Долгих Г. В. Расчет нежестких дорожных одежд по критерию безопасных давлений на глинистые грунты земляного полотна // Автореф. Дис. канд. техн. наук. — Омск: СибАДИ. — 2014. — 20 с.

23. Долгих Г. В. Расчет грунтов земляного полотна по критерию безопасных давлений // Вестник Сибирской государственной автомобильно-дорожной академии. — 2013. — № 6 (34). — С. 43–49.

24. Александров А. С., Киселева Н. Ю. Пластическое деформирование гнейс- и диабаз материалов при воздействии повторяющихся нагрузок // Известия высших учебных заведений. Строительство. — 2012. — № 6. — С. 49–59.

25. Александров А. С. Пластическое деформирование гранодиоритового щебня и песчано-гравийной смеси при воздействии трехосной циклической нагрузки // Инженерно-строительный журнал. — 2013. — № 4 (39) — С. 22–34.

26. Александров А. С. Обобщающая модель пластического деформирования дискретных материалов дорожных конструкций при воздействии циклических нагрузок // Строительные материалы. 2016. № 5. С. 27–30.

27. Кузин Н. В. Расчет пластических смещений асфальтобетонных порожных покрытий // Молодой ученый. — 2016. — № 10 (114). — С. 253–255.

28. Кузин Н. В. Исследование пластичности дорожных асфальтобетонов // Молодой ученый. — 2016. — № 10 (114). — С. 255–257.

29. Александрова Н. П., Александров А. С., Чусов В. В. Учет поврежденности структуры асфальтобетона в критериях прочности и условиях пластичности // В сборнике: Политранспортные системы материалы VIII Международной научно-технической конференции в рамках года науки Россия — ЕС. Новосибирск: СГУПС, 2015. — С. 219–225.

30. Александрова Н. П., Александров А. С., Чусов В. В. Модификация критериев прочности и условий пластичности при расчетах дорожных одежд // Вестник Сибирской государственной автомобильно-дорожной академии. — 2015. № 1 (41). — С. 47–54.

31. Чусов В. В. Модифицированные критерии Писаренко-Лебедева и Кулона-Мора, учитывающие меры теории накапливания повреждений // Молодой ученый. — 2016. — № 9 (113). — С. 338–341.

32. Aleksandrova N. P. Chysow V. V. The usage of integral equations hereditary theories for calculating changes measures in the theory of damage when exposed to repeated loads //// Magazine of Civil Engineering, 2016, No.2. Article in Press.

33. Чусов В. В. Применение теории накапливания повреждений в условиях пластичности асфальтобетона для расчета дорожных покрытий по сопротивлению сдвигу // Молодой ученый. — 2016. — № 6 (110). — С. 221–227.