Методы подавления счетного шума при решении задач физики плазмы методами частиц



В данной работе рассматривается решение самосогласованной задачи моделирования интенсивного потока заряженных частиц в плоском диоде итерационным методом с моделью трубок тока и методом частиц в ячейках. Изучается влияние методов подавления счетного шума, а также способа создания начального распределения модельных частиц на решения, получаемые при решении стационарной самосогласованной задачи на примере плоского диода.

Ключевые слова: метод частиц в ячейках, итерационный метод с моделью трубок тока, подавление шума, самосогласованная задача о плоском диоде

Введение.Наиболее широко используемым инструментом изучения плазмы и динамики потоков заряженных частиц в эмитирующих установках является метод частиц в ячейках [7,9]. Идея метода заключается в том, что плазма представляется как набор большого количества взаимодействующих частиц. Расчетная область разбивается сеткой, в узлах которой хранится информация об электромагнитном поле, плотности тока и заряда. Метод частиц в ячейках естественным образом моделирует процесс движения частиц, учитывая их собственное влияние друг на друга через сеточные величины. Однако для моделирования стационарного состояния пучка более экономичным является итерационный метод с моделью трубок тока [1,3], основанный на итерационном повторении процесса расчета лишь для одного поколения частиц, что позволяет заметно сократить время решения задачи.

Одним из главных недостатков методов частиц является возникновение счетных «нефизических» шумов [8], приводящих к искажению решения. Основной причиной их возникновения является дискретная природа самих методов (представление среды в виде конечного числа частиц). Самым простым способом уменьшения численных шумов является увеличение числа модельных частиц, что ведет к резкому увеличению требуемых вычислительных ресурсов. Для уменьшения счетных шумов [2] изменяют схему раздачи заряда частиц, подбирают оптимальные временной шаг и размер ячейки расчетной сетки. Начальное распределение частиц также играет немаловажную роль. Наиболее распространенными подходами распределения частиц являются схемы тихого и случайного старта. Принцип случайного старта заключается в случайном распределении частиц в фазовом пространстве. Использование схемы «тихого» старта обеспечивает снижение шума и неопределенности случайного старта. Область эмиссии покрывается набором частиц так, чтобы воспроизвести необходимое распределение. Однако широкого распространения схема «тихий старт» не получила [7] по следующим причинам: подход требует большего количества модельных частиц (особенно, в случае начальной дискретизации по множеству измерений), также использование регулярно расположенного множества частиц может привести к появлению «нефизических» корреляций среди частиц.

Постановка задачи. Пусть — двумерная расчетная область, где – граница расчетной области. Вычисление потенциала и напряженности электрического поля для стационарного потока заряженных частиц сводится к решению уравнения Пуассона

(1)

В (1) – оператор Лапласа, — потенциал электрического поля, — напряженность электрического поля, — вектор фазовых координат, – распределение плотности заряда, — функция, описывающая потенциал на электродах, – диэлектрическая проницаемость среды, — нормаль к границе

Предполагается, что задача имеет стационарное решение, тогда выполняется уравнения неразрывности плотности тока

(2)

Плотность тока эмиссии в задаче считается постоянной и определяется из закона Чайлда [4]

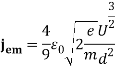(3)

В (3) и — заряд и масса частицы, — расстояние между катодом и анодом, — напряжение на аноде.

Движение заряженной частицы в релятивистском случае описывается следующими уравнениями

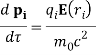
(4)

Здесь — приведенные импульсы частиц, — приведенная энергия частицы, — заряды частиц, — скорости частиц, — масса частиц,– положения частиц, — номер частицы.

Требуется найти решение уравнения движения частиц (4) с учетом (1)-(3), определить распределение электростатического поля и траектории частиц.

Метод частиц в ячейках. Метод [7,9] относится к группе методов «частица-сетка» [5] и объединяет в себе эйлеров и лагранжев подходы моделирования. Движение частиц в методе описывается подвижной лагранжевой сеткой, при этом плотность распределения пространственного заряда и значения электрических полей определены на неподвижной эйлеровой сетке.

Временной шаг метода частиц в ячейках состоит из четырех основных этапов. На первом этапе происходит инжекция новых частиц в расчетную область. На втором этапе происходит расчет движения частиц в электромагнитных полях и раздача плотности заряда, создаваемой частицами, в узлы расчетной сетки. На третьем этапе решаются уравнения поля, определяется новая конфигурация электромагнитных полей. На последнем этапе происходит интерполяция сил, действующих на частицу. На следующем временном шаге все этапы повторяются.

Итерационный метод смоделью трубок тока. Вотличие от метода частиц в ячейках, итерационный метод [1,3] используется только для моделирования стационарных потоков заряженных частиц. метода состоит из следующих этапов. Сперва происходит инжекция частиц в расчетную область. Затем рассчитываются полные траектории частиц под действием электромагнитных полей, рассчитанных на предыдущей итерации. На каждом временном шаге плотность заряда от частиц накапливается в узлах расчетной сетки. После того как все частицы покинут расчетную область, рассчитывается новая конфигурация электромагнитных полей. Процедура повторяется до сходимости к стационарному решению. Требуемое число модельных частиц при расчете итерационным методом значительно меньше по сравнению с методом частиц в ячейках, что делает его более эффективным способом изучения стационарного состояния пучка.

Сглаживание пространственного заряда

Линейные сглаживающие фильтры. Простейшим способом сглаживания является применение линейных сглаживающих фильтров. Их сущность заключается в усреднении значений элементов по их окрестности. Для вычисления значения используется матрица, называемая ядром свертки, содержащая весовые коэффициенты. В данной работе ядро свертки заполняется по закону нормального распределения.

Частотная фильтрация. Фильтрация в частотной области [6,10] основана на применении к пространственному заряду преобразования Фурье и состоит из следующих этапов:

1. Прямое двумерное преобразование Фурье для получения спектра пространственного заряда
2. Центрирование Фурье образа и его умножение на частотную функцию фильтра
3. Обратное двумерное преобразование Фурье

Сглаживающий кубический сплайн. Сглаживающий сплайн определяется как сплайн, минимизирующий следующий функционал:

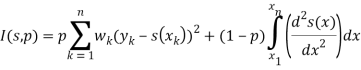(5)

где — приближаемые данные, — веса данных, — сглаживающий параметр. При сглаживающий сплайн превращается в обычный кубический сплайн, при данные аппроксимируются в смысле метода наименьших квадратов.

Результаты. Рассмотрим задачу моделирования плоского диода в случае двумерной декартовой геометрии. Значения основных параметров диода приведены в таблице 1. Расчеты проводились на сетке размерностью .

Таблица 1

Параметры тестового диода

Расстояние от катода до анода, м
Длина, м
Длина эмиттера, м
Напряжение на аноде, В
Плотность тока эмиссии, А/м

Тихий старт. Сравнение методов. При начальном распределении электронов по схеме тихого старта итерационный метод показал хорошую сходимость. Была проведена серия расчетов при , количество модельных частиц — 500. В качестве критерия остановки итерационного процесса использовался

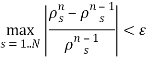(6)

где — количество узлов сетки, — наперед заданная точность.

Результаты расчета с помощью метода частиц в ячейках и итерационного метода достаточно точно согласуются (рис. 1). Однако, так как метод частиц в ячейках требует пересчет электрических полей на каждом временном шаге, расчет с помощью итерационного метода происходит значительно быстрее.

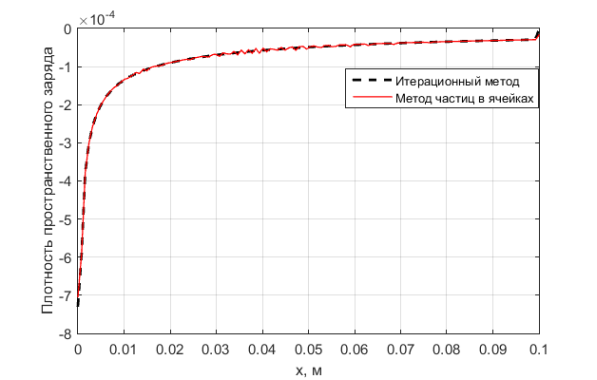
Рис. 1: Распределение плотности пространственного заряда в середине диода

Случайный старт. Случай итерационного метода. Использование схемы случайного старта приводит к появлению больших осцилляций в распределении плотности пространственного заряда. В случае итерационного метода сходимости по критерию (6) добиться не удалось, сглаживание пространственного заряда также не помогло добиться сходимости (рис.2).

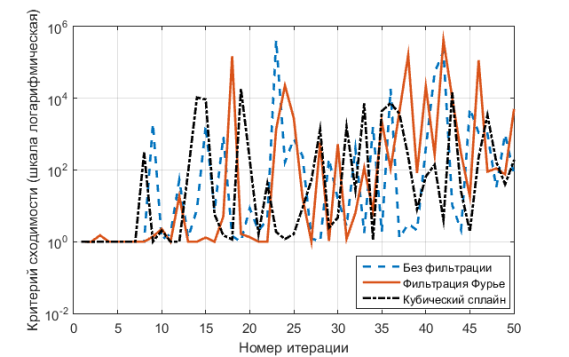
Рис. 2: Большие осцилляции в плотности пространственного заряда приводят к расходимости итерационного метода

Случайный старт. Случай метода частиц в ячейках. Рассмотрим теперь влияние случайного старта при расчетах методом частиц в ячейках. Исследуем также эффективность сглаживания пространственной плотности заряда в методе частиц в ячейках. Для оценки точности расчетов будем использовать решение итерационного метода, полученное со схемой «тихий старт» как эталонное.

На рис. 3 представлено сравнение отклонений распределений пространственного заряда со сглаживанием кубическими сплайнами и без от эталонного решения. На рис. 4 произведено сравнение эффективности алгоритмов сглаживания, результаты представлены как величина среднего отклонения от эталонного значения.

Таким образом, применение сглаживания к пространственной плотности заряда при расчете методом частиц в ячейках, позволяет заметно уменьшить осцилляции, вносимые случайным стартом, тем самым улучшив результаты расчета.

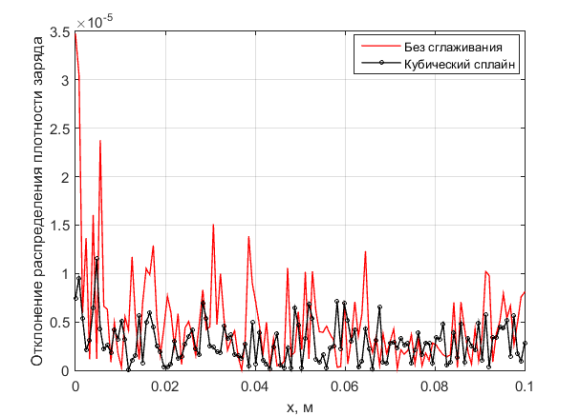
Рис. 3: Отклонение распределения плотности заряда со сглаживанием кубическими сплайнами s=0.5 и без от эталонного решения, полученного итерационным методом

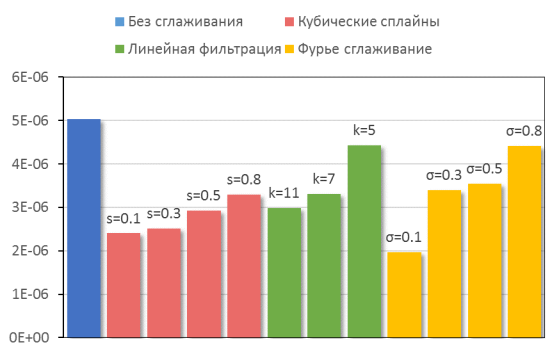
Рис. 4: Сравнение эффективности алгоритмов сглаживания

На диаграмме представлено сравнение среднего отклонения пространственного заряда от эталонного значения, рассчитанного итерационным методом с тихим стартом.

Примечание: где s — сглаживающий параметр кубических сплайнов,

k — размер ядра свертки линейного сглаживания,

σ — параметр оконной функции Гаусса при сглаживании.

Заключение. Итерационный метод с моделью трубок тока является более экономичным и эффективным, по сравнению с методом частиц в ячейках, инструментом моделирования стационарных состояний пучка частиц в случае отсутствия необходимости дискретизации начальных данных по множеству измерений. Использование случайного начального распределения модельных частиц в итерационном методе приводит к большим колебаниям в распределении пространственного заряда и расходимости метода. При расчете методом частиц в ячейках подавление счетного шума сглаживанием пространственной плотности заряда позволяет заметно улучшить точность расчета, снизив осцилляции, вносимые случайным стартом.

Литература:

1. Алцыбеев В. В. Оптимизационный алгоритм расчета плотности тока эмиссии // Вестник Санкт-Петербургского университета. Серия 10. Прикладная математика. Информатика. Процессы управления. 2015. № 4. С. 56–72
2. Месяц, Е. А. Методы оценки и повышения точности решения задач физики плазмы методом частиц в ячейках: Ph.D. thesis / Институт вычислительной математики и математической геофизики СО РАН. — Новосибирск, 2014–110 с.
3. César C. Xavier and Cláudio C. Motta. The XMGUN Particle Path FEM Code IEEE Transactions on Magnetics, vol. 46, No. 8, August 2010
4. Child, C. D. Discharge from hot cao / C. D. Child // Phys. Rev. Series I. —
5. 1911. — Vol. 32, № 5. — pp. 255–282.
6. Hockney, R. Computer Simulation Using Particles / R. Hockney, J. Eastwood. — Francis, 1988. — 540 pp.
7. Jolliet S., Bottino A., Angelino P., et al. A global collisionless PIC code in magnetic coordinates // Computer Physics Communications. — 2007. —Vol. 177. — P. 409–425.
8. Lapenta G., Particle In Cell Method A brief description of the PIC Method // Centrum voor Plasma Astrofysica Katholieke Universiteit Leuven
9. Mesyats E. A. A noise-reducing algorithm for Particle-in-Cell plasma simulation // Bull. Nov. Comp. Center, Num. Anal., 14 (2009), pp. 21–30
10. Mudiganti, J. C. An Emission Model for the Particle-in-Cell Method: Ph.D. thesis / Darmstadt: TU Darmstadt. — 2006. — 123 pp.
11. Sydora R. D. Low-noise electromagnetic and relativistic Particle-in-Cell plasma simulation models // J. Comp. Appl. Math.. — 1999.. — Vol. 109.. —P. 243–259.