Рассматривается модель вертикальной дифференциации на рынке страхования, предложенная и исследованная в работах [4], [5], [6], [7], [8]. Фирма монополист предлагает потребителям услуги различного качества и цен, при этом каждый потребитель выбирает страховую услугу, максимизируя собственную функцию потребительского излишка, и единственный параметр неоднородности потребителей — вероятность наступления страхового случая.
Ключевые слова: страхование, вертикальная дифференциация, монополия, задача нелинейного программирования
Неотъемлемой частью современной экономики является сфера страхования. Человеческая жизнь устроена так, что невозможно исключить возникновение непредвиденных ситуаций, вызванных явлениями природы или обстоятельствами, которые не зависят от воли и желания человека. Эти неблагоприятные события, среди которых наиболее распространены стихийные бедствия и несчастные случаи, могут привести к значительным материальным убыткам, ущербу здоровья или потере трудоспособности. Отсюда возникает необходимость поиска путей минимизации указанных потерь, что и обусловило появление и развитие страхования.
Базовые предпосылки модели.
-
Потребители формируют собственные оценки качества
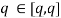 предлагаемых им услуг, которые играют роль как в определении верхней границы цены
предлагаемых им услуг, которые играют роль как в определении верхней границы цены 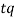 , приемлемой для данных потребителей, так и в выборе конкретной услуги из качества доступных или отказаться от всех.
, приемлемой для данных потребителей, так и в выборе конкретной услуги из качества доступных или отказаться от всех.
-
Потребители в разной степени готовы платить большую цену за повышение качества предлагаемых услуг. Обозначим за
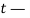 параметр, определяющий вероятность страхового случая потребителя:
параметр, определяющий вероятность страхового случая потребителя:
![]()
-
Множество стратегий фирмы — это всевозможные вектора
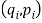 , где
, где 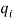 — качество предлагаемых услуг,
— качество предлагаемых услуг, 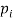 — цена
— цена 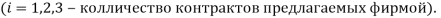
На первом этапе фирма выбирает уровни качества ![]() . При этом
. При этом
![]() .....................................................(1)
.....................................................(1)
C точки зрения потребителей услуги являются заменителями, и в рассматриваемый промежуток времени потребитель может приобрести не более одной услуги.
На втором шаге фирма, назначает цены на свои услуги ![]() соответственно.
соответственно.
Каждый потребитель из числа S (далее будем считать, что ![]() ) стремится максимизировать свою функцию потребительского излишка следующего вида:
) стремится максимизировать свою функцию потребительского излишка следующего вида:
где ![]() — параметр, который показывает вероятность страхового случая потребителя. Чем больше вероятность страхового случая, тем большую цену готов заплатить потребитель за услуги страхования. t — случайная величина, равномерно распределённая на отрезке
— параметр, который показывает вероятность страхового случая потребителя. Чем больше вероятность страхового случая, тем большую цену готов заплатить потребитель за услуги страхования. t — случайная величина, равномерно распределённая на отрезке ![]() . Цель фирмы — максимизация прибыли от реализации своих услуг за рассматриваемый период.
. Цель фирмы — максимизация прибыли от реализации своих услуг за рассматриваемый период.
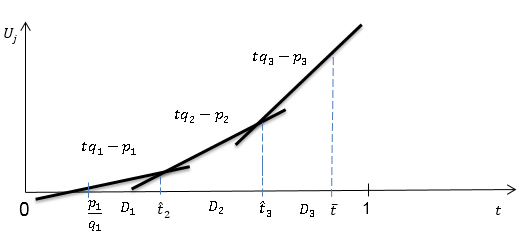
Рис. 1. График самоотбора потребителей
Точки ![]() и
и ![]() на Рис. 1. отвечает потребителям, которым покупка услуги с той или иной ценой в равной степени привлекательна.
на Рис. 1. отвечает потребителям, которым покупка услуги с той или иной ценой в равной степени привлекательна.
Все потребители, для которых параметр 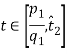 , выберут услуги по цене
, выберут услуги по цене ![]() , все потребители, для которых параметр
, все потребители, для которых параметр ![]() , выберут услуги по цене
, выберут услуги по цене ![]() , а все потребители, для которых параметр
, а все потребители, для которых параметр ![]() , выберут услуги по цене
, выберут услуги по цене ![]() . Так как доли рынка должны быть неотрицательны, необходимо ввести ограничение:
. Так как доли рынка должны быть неотрицательны, необходимо ввести ограничение:
![]() .......................................................(2)
.......................................................(2)
Функция ожидаемой прибыли фирмы будет выглядеть:
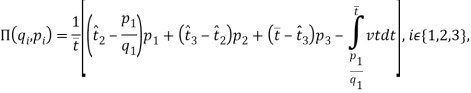 .....................................................(3)
.....................................................(3)
учитывая (2).
Где ![]() — средний размер страхового возмещения, а
— средний размер страхового возмещения, а ![]() — ожидаемые затраты по сопровождению страхового случая потребителя с параметром
— ожидаемые затраты по сопровождению страхового случая потребителя с параметром ![]() (costoftheclaimshandingprocedure).
(costoftheclaimshandingprocedure).
Поиск оптимальных контрактов.
Чтобы максимизировать функцию прибыли (3), используем попятно-рекуррентную процедуру, начиная со второго шага (нахождения вектора оптимальных цен).
Составим и решим систему
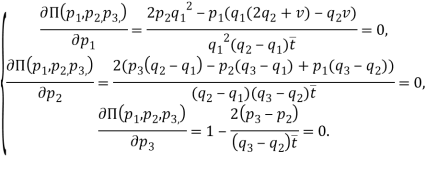
Эта система имеет единственное решение:
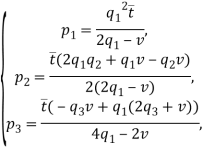
которое является точкой максимума функции ожидаемой прибыли ![]() при условиях (1) и
при условиях (1) и ![]() .
.
Теперь рассмотрим первый этап (поиск оптимальных качеств). Функция ожидаемой прибыли ![]() ,
,![]() ), может быть записана в виде:
), может быть записана в виде:
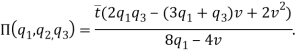
Как можно заметить, ![]() не зависит от
не зависит от ![]() . Производная
. Производная
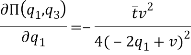
строго отрицательна, а производная
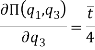
строго положительна. Следовательно, оптимальный уровень качества ![]() есть
есть ![]() а оптимальный уровень качества
а оптимальный уровень качества ![]() есть
есть![]() .
.
Таким образом, функция прибыли ![]() будет выглядеть следующим образом
будет выглядеть следующим образом
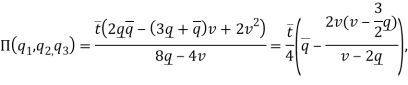 .....................................................(4)
.....................................................(4)
что является результатом при рассматривании двух контрактов, полученное в [4].
Таким образом, можно сделать вывод, что фирме не имеет смысла предлагать три контракта.
Рассмотрим альтернативное решение задачи максимизации функции прибыли ![]() . Обозначим ограничения
. Обозначим ограничения ![]() следующим образом:
следующим образом:
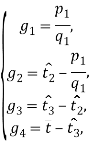
и воспользуемся теоремой Куна-Таккера.
Рассмотрим ЗНП:
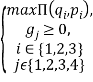 .......................................................(5)
.......................................................(5)
Условие регулярности в ЗНП считается выполненным. Пусть ![]() — оптимальное решение (19). Следовательно,
— оптимальное решение (19). Следовательно, ![]() удовлетворяет условиям Куна-Таккера:
удовлетворяет условиям Куна-Таккера:
-
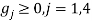 — условие допустимости.
— условие допустимости.
-
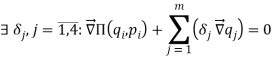 — условие оптимальности.
— условие оптимальности.
-
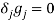 — условие дополняющей нежесткости.
— условие дополняющей нежесткости.
Составим функцию Лагранжа для данной задачи:
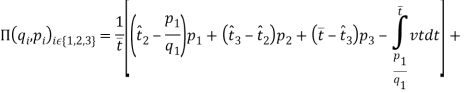
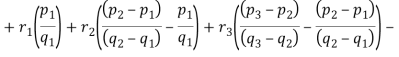
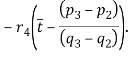
Решая задачу нелинейного программирования было получено решение (4).
Заключение.
Был изучен вопрос о целесообразности применения фирмой монополистом трёх различных контрактов в условиях добровольного страхования. Задача была решена двумя способами: с помощью попятно-рекуррентной процедуры [2], и используя теорему Куна-Таккера [1]. Из приведённых решений можно сделать вывод, что такое поведение не принесет фирме больше прибыли, чем при использовании фирмой двух контрактов.
Литература:
- Васильев Ф. П. Методы оптимизации. М.: Факториал Пресс, Гл. ред. ФИЗМАТЛИТ, 2002. 824 c.
- Петросян Л. А., Кузютин Д. В. Устойчивые решения позиционных игр. СПб.: Издательство СПбГУ, 2008. 326 c.
- Kuzyutin D. V., Nikitina M. V., Smirnova N. V., Razgulyaeva L. N. The vertical differentiation model in the insurance market: costs structure and equilibria analysis // Contributions to Game Theory and Management, 2015. P. 176–186
- Okura M. The vertical differentiation model in the insurance market // International Journal of Economics and Business Modeling, 2010. № 1(2). P. 12–14.
- Schlesinger H., Schulenburg J. Search costs, switching cost and product heterogeneity in an insurance market // M. G. V. D. Journal of Risk and Insurance, 1991. № 58. P. 109–119.
- Schlesinger H., Schulenburg J. Consumer information and decisions to switch Insurers. // M. G. V. D. Journal of Risk and Insurance, 1993. № 60. P. 591–615.
- Tirole J. The theory of industrial organization. Cambridge: The MIT Press, MA. 1988. 943 p.







