Введение в вейвлет анализ. Вейвлет преобразование в настоящее время нашло обширное применение в электроэнергетике в такие направления, как анализ качества электроэнергии, релейная защита электроэнергетических систем расчёты переходных процессов, диагностика электрического оборудования.
Вейвлеты были введены в конце 1980-х. Впервые термин «вейвлет» вввели Ж. Морлеи А. Гроссман. «Wavelet» в переводе на английский язык с французского слова «ondelette» означает «короткая волна». Также можно встретить в литературе такой перевод как «всплеск», «выброс» [1].
Согласно [2], вейвлетами называют особые функции, которые представляют собой малые волновые пакеты, имеющие значение интеграла равным нулю, локализацию по оси переменной (t или x), способность к сдвигу и масштабированию (сжатию или растяжению).
Масштабирование и сдвиг происходит согласно следующей формуле
, (1)
где 
- это исходный (материнский вейвлет) из которого образован 
, благодаря операциям изменения временного масштаба (a) и сдвига во времени (b); 
- это масштабирующее число, а множитель 
обеспечивает независимость нормы функции от масштабирующего числа.
Рассмотрим в качестве примера вейвлет функцию и модуль спектральной плотности этой функции (рисунок 1).
«Малые значения параметра а соответствуют мелкому масштабу вейвлет функции или высоким частотам (ω ~ 1/a), большие значения a — крупному масштабу вейвлет функции » [3]. Иначе говоря, мы растягиваем исходный вейвлет 
и сжимаем его спектр.
Если рассматривать частотную область, то спектры вейвлетов напоминают, так называемые, всплески или волночки. (Именно из-за этого обстоятельства встречаются и такие варианты перевода слова wavelet на русский язык, как «волночка»). Они (всплески и волночки) имеют пик на частоте 
и полосу 
(полосовой фильтр); при этом величины 
и 
снижаются при увеличении параметра .
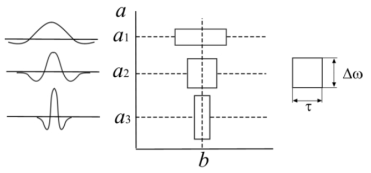
Рис.1. Масштабирование вейвлет функций
На данный момент существует большое количество типов вейвлетов.
Все материнские вейвлеты можно разделить на три группы.
- Вещественные непрерывные вейвлеты. К ним относятся Гаусовы первого порядка, или WAWE- вейвлет, второго порядка, или MHAT-вейвлет «мексиканская шляпа- mexicanhat», n- ого порядка; DOG- differenceofgaussians; LP- LittlewoodandPaley.
- Вещественные дискретные вейвлеты. Это HAAR-вейвлет «вейвлет Хаара» и FHAT- вейвлет «французская шляпа-frenchhat».
- Комплексные вейвлеты. К этой группе относятся вейвлет Морле (Morlet) и вейвлет Пауля (Paul) [3].
Рассмотрим более подробнее наиболее часто встречающиеся в литературе.
Вейвлет Хаара.
Вейвлет Хаара можно назвать самым простым типом вейвлета и наиболее распространённым. Но он имеет пару недостатков, к которым можно отнести негладкость и несимметричность формы в t-области. Однако хорошо локализован во временной области. HAAR- вейвлет можно представить следующей ступенчатой функцией
Графическое представление вейвлета Хаара на рисунке 2.
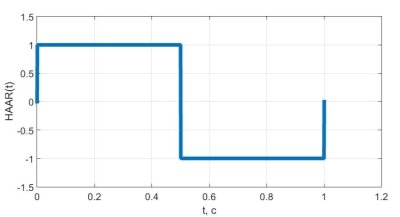
Рис. 2. Вейвлет функция Хаара
Но большинство типов вейвлетов не имеют аналитической записи функции в явном виде одной формулой. И поэтому они задаются итерационными выражениями. Примером такого вида вейвлетов является функции Добеши (Daubechies). Которые являются одними из самых известных, ввиду того, что Игрид Добеши внесла огромный вклад в развитии теории вейвлетов. Они широко используются в практике и являются несимметричными.
Графическое представление вейвлета Добеши представлено на рисунке 3.
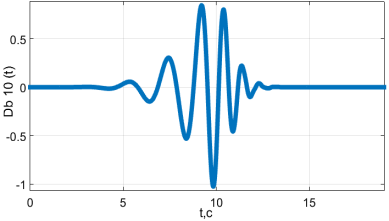
Рис. 3. Вейвлет Добеши 10 порядка
Кроме ранее рассмотренных вейвлетов имеются ещё вейвлеты, входящие в пакет WaveletToolbox. Это вейвлет Симплета, биортогональный вейвлет, вейвлет Шеннона, вейвлет Мейера, вейвлет Койфлетса.
У любого типа вейвлета есть свои преимущества и недостатки. Поэтому какой вейвлет лучше использовать зависит от поставленной задачи и от анализируемого сигнала.
Применение преобразования Фурье для анализа сигналов.
Если применить преобразование Фурье для анализа стационарных сигналов тока и напряжения, то результат точно отражает картину, происходящую в сигнале. Однако всё не атк просто, если рассматривать нестационарные сигналы.
Нестационарным называется сигнал тока, в котором присутствуют различные частоты на разных временных интервалах. Смоделируем нестационарный сигнал тока (рисунок 4, рисунок 5).
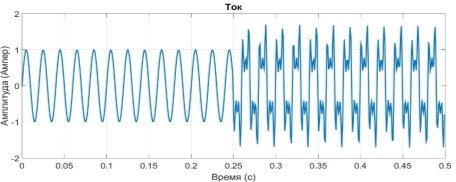
Рис. 4. Нестационарный сигнал тока
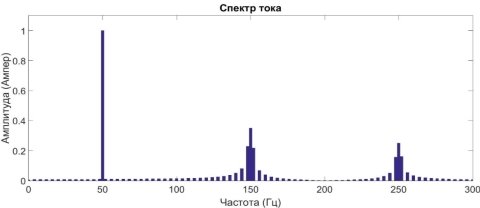
Рис. 5. Спектральный состав нестационарного сигнала тока
Из полученных графиков видно, что имеются два временных промежутка, первый от 0 до 0,25 с, второй от 0,25с. до 0,5с. На первом временном интервале присутствует частота f=50 Гц, на втором временном интервале присутствуют частоты f=50 Гц, f=150 Гц и f=250 Гц.
Мы видим, что в случае нестационарного сигнала существует растекание спектра, с которым преобразование Фурье не справляется. Проблему растекания спектра можно решить с помощью оконного Преобразования Фурье. Но сложность при использовании оконного преобразования Фурье заключается в подборе ширины оконной функции.
В настоящее время большую популярность для анализа нестационарных режимов в электроэнергетике приобрело вейвлет преобразование. Так как оно решает те недостатки, которые присуще преобразованию Фурье.
Вейвлет преобразования для расчёта действующих значений величин.
Существует несколько видов вейвлет преобразований: непрерывное вейвлет преобразование, дискретное вейвлет преобразованеи, диадное вейвлет преобразование.
В основе вейвлет преобразования лежат две непрерывных и зависящих друг от друга функции (вейвлет функция и масштабирующая функция).
Для реализации применения вейвлет преобразования для расчёта действующих значений токов и напряжений зададим напряжения и токи в виде:
, (2)
, (3)
, (4)
; (5)
; (6)
. (7)
где 
- фазное напряжение 50 Гц; 
- фазное напряжение 250 Гц; 
- фазное напряжение 350 Гц; 
, 
, 
- ток первой, пятой и седьмой гармоники.
Рассчитаем действующие значения двумя способами аналитически и по вейвлет коэффициентам. Используя дискретное вейвлет преобразование и программынйы комплекс MATLAB. Погрешность рассчитана между самым точным типом вейвлета и значением вычисленным аналитически. Результаты сведём в таблицу 1.
Таблица 1
Расчёт действующих значений токов инапряжений
|
Величина |
Расчётное значение |
Расчет по вейвлет коэффициентам |
Погрешность |
|||
|
Haar |
db 10 |
db24 |
db42 |
|||
|
|
30 |
27,448 |
29,987 |
29,998 |
30 |
0 |
|
|
5 |
1,864 |
4,917 |
4,992 |
4,999 |
0,0002 |
|
|
3 |
7,968 |
2,650 |
2,866 |
2,945 |
0,018 |
|
|
220 |
199,376 |
219,979 |
220 |
219,989 |
0,0001 |
|
|
4 |
13,233 |
3,893 |
3,994 |
3,999 |
0,0003 |
|
|
3 |
39,06 |
2,7282 |
2,8658 |
2,9454 |
0,018 |
|
Примечание
|
||||||
, А
, А
, А
, А
, А
, А
, 
, 
- действующие значений тока первой, пятой и седьмой гармоники.
, 
, 
- действующие значений напряжения первой, пятой и седьмой гармоники.
Вывод. Вейвлет преобразование мощный инструмент для анализа сигналов в электроэнергетике, так как анализ качества электроэнергии является важным фактором и правильное определение параметром режима имеет большое значение. При сравнении результатов действующих значений токов первой, пятой и седьмой гармоник и действующих значений напряжения первой, пятой и седьмой гармоник получили погрешность не превысила 1 %. Можно сделать вывод, что чем больше порядок используемого вейвлета, тем точнее получаются результаты.
Литература:
- Нагорнов, О. В. Вейвлет-анализ в примерах [Текст]: учебное пособие / О. В. Нагорнов, В. Г. Никитаев, В. М. Простокишин,С. А. Тюфлин и др. — М.: НИЯУ МИФИ. — 2010. — 120 с.
- Дьяконов, В. П. От теории к практике. Вейвлеты [Текст]: учебное пособие / А. Н. Дьяконов. — М: Салон-Р. — 2003. — 440 с.
- Яковлев, А. Н. Введение в вейвлет-преобразование [Текст]: учебное пособие / А. Н. Яковлев. — Новосибирск: Изд-во НГТУ. — 2003. — 104 с.
