Цель данной статьи — проиллюстрировать на примерах основные определения и результаты из [1]. Основная задача, рассматриваемая в [1] — является ли граф суперэйлеровым, т. е., по определению, содержит ли граф остовный эйлеров подграф.
За ![]() далее обозначается множество вершин графа
далее обозначается множество вершин графа ![]() . За
. За ![]() – множество рёбер графа
– множество рёбер графа ![]() . За
. За ![]() – степень вершины
– степень вершины ![]() в графе
в графе ![]() .
.
Понятие суперэйлеровости будет рассмотрено через понятие стягиваемых подграфов: если ![]() – стягиваемый подграф
– стягиваемый подграф ![]() , тогда суперэйлеровость
, тогда суперэйлеровость ![]() равносильна суперэйлеровости
равносильна суперэйлеровости ![]() . Это сужает проблему суперэйлеровых графов.
. Это сужает проблему суперэйлеровых графов.
Итак, введём понятие стягиваемого подграфа. Подграф ![]() графа
графа ![]() называется стягиваемым (collapsible), если для любого чётного подмножества его вершин
называется стягиваемым (collapsible), если для любого чётного подмножества его вершин ![]()
![]() содержит связный подграф, множество вершин с нечетными степенями которого есть
содержит связный подграф, множество вершин с нечетными степенями которого есть ![]() .
.
Пример (стягиваемого подграфа).
Рассмотрим граф ![]() . Пусть
. Пусть ![]() (рис. 1). Любое чётное подмножество его вершин
(рис. 1). Любое чётное подмножество его вершин ![]() – это либо пустое множество, либо две соседние вершины (рис. 2). Содержит ли
– это либо пустое множество, либо две соседние вершины (рис. 2). Содержит ли ![]() связный подграф, множество вершин с нечётными степенями которого есть
связный подграф, множество вершин с нечётными степенями которого есть ![]() ? Да, содержит – соответствующий подграф выделен на рис 3. Следовательно, рассмотренный пример представляет собой пример стягиваемого подграфа.
? Да, содержит – соответствующий подграф выделен на рис 3. Следовательно, рассмотренный пример представляет собой пример стягиваемого подграфа.
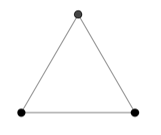
Рис. 1. ![]()
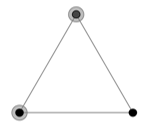
Рис. 2.![]()
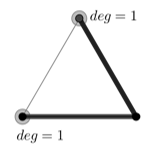
Рис. 3.
Пример нестягиваемого подграфа.
Приведём пример нестягиваемого подграфа, что проиллюстрирует существенность введённого определения. Пусть снова ![]() (рис. 4). Возьмем чётное подмножество вершин
(рис. 4). Возьмем чётное подмножество вершин ![]() (рис. 5), для которого не найдется в
(рис. 5), для которого не найдется в ![]() связного подграфа, множество вершин с нечетными степенями которого есть
связного подграфа, множество вершин с нечетными степенями которого есть ![]() . Чтобы попасть в вершину
. Чтобы попасть в вершину ![]() необходимо пройти по угловой вершине, но степень этой вершины будет четной (рис. 6). Значит, она не попала бы в Х.
необходимо пройти по угловой вершине, но степень этой вершины будет четной (рис. 6). Значит, она не попала бы в Х.
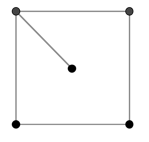
Рис. 4. ![]()
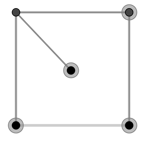
Рис. 5.![]()
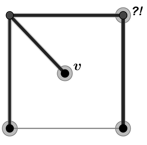
Рис. 6.
Введем определение S-подграфа. Для чётного подмножества вершин ![]() S-подграфом графа
S-подграфом графа ![]() называется подграф
называется подграф ![]() такой, что
такой, что ![]() связен, и
связен, и ![]() состоит из таких вершин
состоит из таких вершин ![]() , степень которых в
, степень которых в ![]() нечётна.
нечётна.
Запишем кратко все условия, за выполнением которых необходимо следить при работе с этим определением:
![]() ,
,
![]() связан,
связан,
![]() .
.
Пример S-подграфа приведён на рис. 3. Здесь ![]() .
.
Если для любого чётного подмножества ![]() граф
граф ![]() имеет S-подграф, то
имеет S-подграф, то ![]() называют стягиваемым. И это определение согласуется с определением стягиваемого подграфа, которое было дано выше.
называют стягиваемым. И это определение согласуется с определением стягиваемого подграфа, которое было дано выше.
Граф называется суперэйлеровым, если он содержит остовный (т.е. содержащий все вершины) эйлеров (т. е. содержащий замкнутый путь, проходящий через каждое ребро графа ровно по одному разу) подграф.
Заметим, что из стягиваемости следует эйлеровость. Достаточно в определении S-подграфа взять ![]() , т. к. из этого будет следовать, что граф связен, а степени всех его вершин чётны, из чего следует эйлеровость графа.
, т. к. из этого будет следовать, что граф связен, а степени всех его вершин чётны, из чего следует эйлеровость графа.
Утверждение. Граф ![]() является суперэйлеровым тогда и только тогда, когда
является суперэйлеровым тогда и только тогда, когда ![]() содержит R-подграф. Где
содержит R-подграф. Где ![]() – это множество таких вершин
– это множество таких вершин ![]() , степень которых в
, степень которых в ![]() нечетна, т. е.
нечетна, т. е. ![]() .
.
Пример (иллюстрирующий утверждение).
Рассмотрим граф ![]() – рис 7. Следуя утверждению, выделяем все вершины в
– рис 7. Следуя утверждению, выделяем все вершины в ![]() , степень которых нечетна (рис. 8). Получаем множество
, степень которых нечетна (рис. 8). Получаем множество ![]() . Далее находим R-подграф
. Далее находим R-подграф ![]() графа
графа ![]() . Он изображён на рис 9. Видим, что
. Он изображён на рис 9. Видим, что ![]() (рис. 10) и есть остовный эйлеров подграф графа
(рис. 10) и есть остовный эйлеров подграф графа ![]() , что и влечёт суперэйлеровость
, что и влечёт суперэйлеровость ![]() .
.
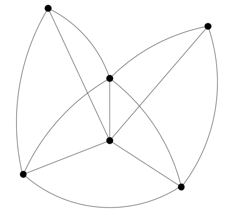
Рис. 7. ![]()
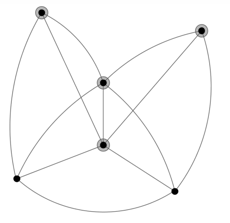
Рис. 8. ![]()
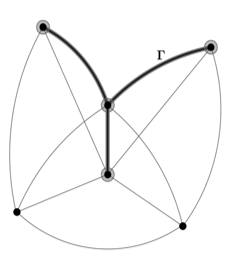
Рис. 9. Г – R-подграф
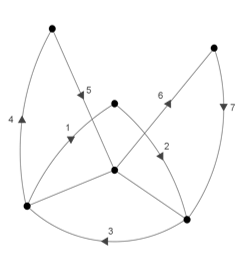
Рис. 10. ![]()
Теорема 1. Пусть ![]() – граф и
– граф и ![]() . Если
. Если ![]() содержит остовное дерево
содержит остовное дерево ![]() такое, что все компоненты
такое, что все компоненты ![]() имеют равное количество вершин в
имеют равное количество вершин в ![]() , то
, то ![]() имеет S-подграф.
имеет S-подграф.
Пример (иллюстрирующий теорему 1).
Рассмотри граф ![]() из предыдущего примера (рис.7). Уже известно, что этот граф имеет R-подграф, значит есть возможность найти остовное дерево
из предыдущего примера (рис.7). Уже известно, что этот граф имеет R-подграф, значит есть возможность найти остовное дерево ![]() из условия теоремы. Такое дерево изображено на рис. 11. При этом
из условия теоремы. Такое дерево изображено на рис. 11. При этом ![]() связен, а значит имеет единственную компоненту. Следовательно, условие теоремы выполнено, значит
связен, а значит имеет единственную компоненту. Следовательно, условие теоремы выполнено, значит ![]() имеет R-подграф, который мы уже предъявили на рис. 9.
имеет R-подграф, который мы уже предъявили на рис. 9.
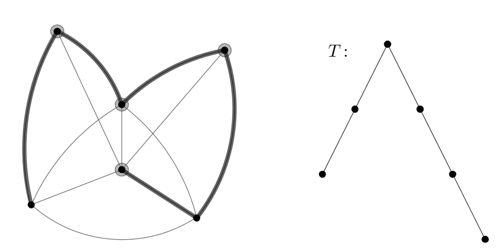
Рис. 11. Остовное дерево ![]()
Теорема 2.
-
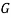 содержит два рёберно непересекающихся остовных дерева.
содержит два рёберно непересекающихся остовных дерева.
-
 стягиваемый.
стягиваемый.
-
 суперэйлеров.
суперэйлеров.
Теорема утверждает, что ![]() .
.
Пример (иллюстрирующий теорему 2).
Теорема 2 представляет собой признак, по которому можно сделать вывод о суперэйлеровости графа – требуется в графе найти два рёберно непересекающихся остовных дерева. Рассмотрим граф из предыдущего примера. Первое остовное дерево ![]() представлено на рис. 11. На рис. 12 представлено ещё одно остовное дерево
представлено на рис. 11. На рис. 12 представлено ещё одно остовное дерево ![]() . Заметим, что приведённые деревья не пересекаются по рёбрам, из чего, согласно теореме 2, вновь можно сделать вывод о суперэйлеровости рассматриваемого графа.
. Заметим, что приведённые деревья не пересекаются по рёбрам, из чего, согласно теореме 2, вновь можно сделать вывод о суперэйлеровости рассматриваемого графа.
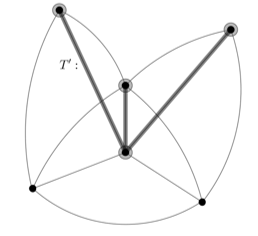
Рис. 12. Остовное дерево ![]()
Пусть ![]() – граф,
– граф, ![]() – его подграф, а
– его подграф, а ![]() – чётное подмножество
– чётное подмножество ![]() . Пусть
. Пусть ![]() – остовный подграф
– остовный подграф ![]() такой, что
такой, что ![]() . Тогда сужением
. Тогда сужением ![]() называется граф, вершины которого – это компоненты
называется граф, вершины которого – это компоненты ![]() . При этом отдельные вершины
. При этом отдельные вершины ![]() инцидентны такому же числу рёбер, как соответствующие компоненты
инцидентны такому же числу рёбер, как соответствующие компоненты ![]() в
в ![]() .
.
Определим ![]() как подмножество, состоящее из тех вершин
как подмножество, состоящее из тех вершин ![]() , которые соответствуют компонентам остовного подграфа
, которые соответствуют компонентам остовного подграфа ![]() с нечётным числом вершин в
с нечётным числом вершин в ![]() .
.
Рассмотрим введённые определения и обозначения на примере.
Пример.
Рассмотрим граф ![]() (рис. 13) и его подграф
(рис. 13) и его подграф ![]() (рис. 14).
(рис. 14).
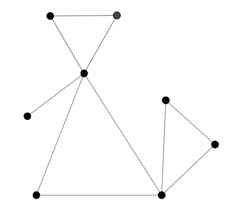
Рис. 13. ![]()
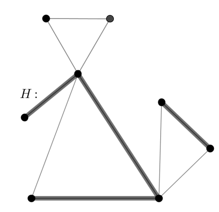
Рис. 14. ![]()
Далее нужен остовный подграф ![]() такой, что
такой, что ![]() . Дополним подграф
. Дополним подграф ![]() двумя вершинами и получим
двумя вершинами и получим ![]() (рис. 15).
(рис. 15).
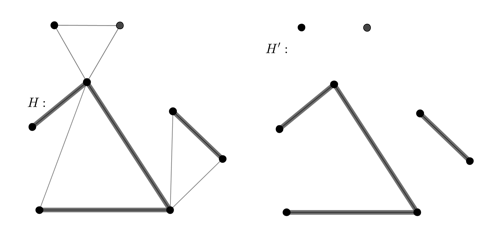
Рис. 15. ![]()
Рассмотрим компоненты ![]() (выделены пунктиром на рис. 16). И то, как они связаны в графе
(выделены пунктиром на рис. 16). И то, как они связаны в графе ![]() (рис. 17).
(рис. 17).
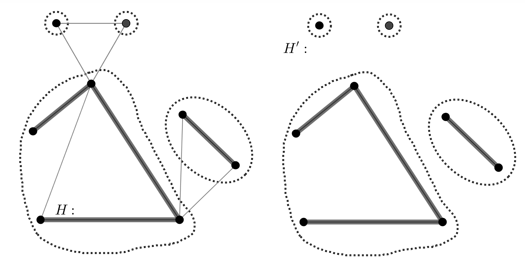
Рис. 16. Компоненты
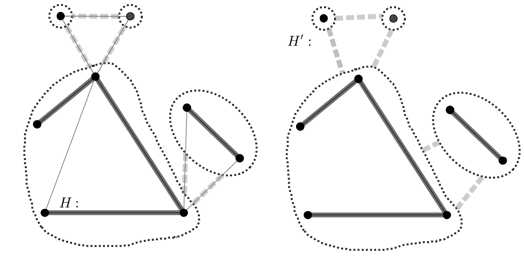
Рис. 17. Связь компонент ![]()
Получим сужение ![]() (рис. 18).
(рис. 18).
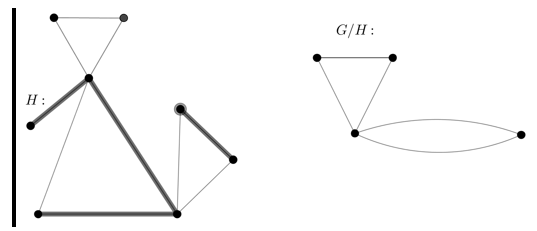
Рис. 18. Сужение ![]()
Теперь разберём понятие ![]() . Возьмём чётное подмножество
. Возьмём чётное подмножество ![]() вершин в
вершин в ![]() . Рассмотрим число вершин в компонентах
. Рассмотрим число вершин в компонентах ![]() . Выделим из них те компоненты, у которых число вершин в
. Выделим из них те компоненты, у которых число вершин в ![]() нечётно. Получаем искомое
нечётно. Получаем искомое ![]() (рис. 19).
(рис. 19).
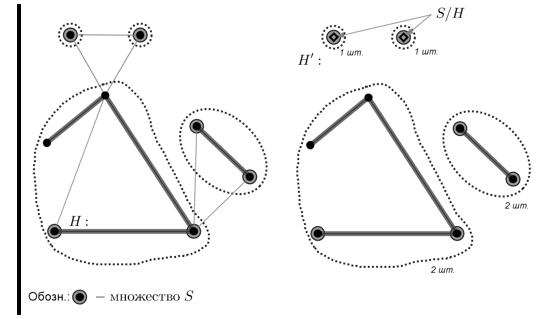
Рис. 19. Сужение ![]()
Теорема 3.
-
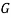 имеет S-подграф.
имеет S-подграф.
-
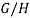 имеет
имеет 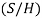 -подграф.
-подграф.
Пусть ![]() – связный подграф
– связный подграф ![]() , и пусть
, и пусть ![]() . Тогда
. Тогда ![]() .
.
Если ещё
Следствие.
Если ![]() стягиваемый подграф
стягиваемый подграф ![]() , то
, то![]() суперэйлеров тогда и только тогда, когда
суперэйлеров тогда и только тогда, когда ![]() суперэйлеров.
суперэйлеров.
Литература:
- P. A. Catlin. Supereulerian graphs, collapsible graphs, and four-cycles // Congressus Numerantium 58 (1987), pp. 233–246.







