В большинстве экономико-математических моделей, сформулированных как задачи линейного программирования, часть или все компоненты вектора-решения должны выражаться в целых числах, т. е. быть целочисленными. К ним относятся, например, задачи, в которых переменные означают количество единиц неделимой продукции, число станков при закупке оборудования, количество домов при очередности строительства и т. д. [3, c. 180]
С другой стороны, это могут быть задачи, в которых при моделировании используются логические (булевы) переменные со значениями 1 и 0, что означает, например, взимать или не взимать арендную плату, создавать или не создавать дополнительный пункт производства и т. д. Покажем особенности фактора целочисленности на следующем примере, который в учебных целях генерируется на компьютере в виде индивидуальных заданий. Оптимальное решение в примере, в принципе, не может быть получено каким-либо округлением решения соответствующей задачи линейного программирования.
Для решения рассмотренного класса задач математического программирования, как правило, используется универсальный метод решения под названием «метод ветвей и границ». [2, с. 158]
Продемонстрируем основные идеи этого метода на примере решения задачи целочисленного линейного программирования (ЦЛП).
Эти задачи включают в себя требования целочисленности ко всем искомым переменным. Они относятся к классу задач полностью целочисленного линейного программирования (задача ЦЛП). В свою очередь, эти задачи являются частным случаем задачи частично целочисленного линейного программирования (ЧЦЛП). [2, с. 160]
При решении задач частично-целочисленного линейного программирования методом ветвей и границ на определенных этапах решаются вспомогательные задачи линейного программирования (ЛП), для которых применяется симплекс-метод.
Рассмотрим развернутую экономико-математическую модель задачи.
Система переменных: x1, x2
Система ограничений: 2x1 + x2 ≤ 9
5x1 + 4x2 ≤ 29
Целевая функция: F = 27x1 + 21x2 → max
Решение задачи осуществляется симплексным методом [1, с. 176] с помощью сервисной функции MS Excel «Поиск решения».
Описание шагов алгоритма «метода ветвей и границ»
- Решение вспомогательной задачи линейного программирования.
Вспомогательная задача № 1 получается из данной задачи целочисленного линейного программирования путём игнорирования требования целочисленности. Решим задачу симплексным методом с помощью Excel. В результате получим: х1=2,3, х2=4,3, Fmax=154 (схема 1).
2.Очередное ветвление вспомогательной задачи на две вспомогательные подзадачи нижнего уровня.
Так как вышеполученное решение нецелочисленное, то оно дает верхнюю границу F = 154 для максимума целевой функции искомого оптимального решения исходной задачи.
В этом случае одна из переменных, имеющих дробное значение, в данном случае x1, берется за основу для разбиения (ветвления) данной вспомогательной задачи № 1 на вспомогательные подзадачи под номерами 1.1 и 1.2 по нижеприведенной методике:
Так как 2 < x1=2,3 < 3, то:
задача 1.1. → задача 1.2.
2x1 + x2 ≤ 9 → 2x1 + x2 ≤ 9
5x1 + 4x2 ≤ 29 → 5x1 + 4x2 ≤ 29
х1<=2 → х>=3
х1>=0, х2>=0х1>=0, х2>=0
F = 27x1+21x2 → max → F = 27x1+21x2 → max
При решении подзадачи 1.1. в Excel добавим ограничение х1<=2
В результате получим:
х1=2, х2=4,75 Fмах=153,75.
153,75 — уточненная верхняя граница
При решении подзадачи 1.2. в Excel добавим ограничение х2>=3
В результате получим:
х1=3, х2=3, Fмах=144
Таким образом, получим первый целочисленный рекорд.
- Проверка оптимальности текущего целочисленного рекорда после очередного ветвления на основе формулировки критерия оптимальности текущего целочисленного рекорда по методу ветвей и границ:Текущий целочисленный рекорд объявляется оптимальным решением исходной задачи в том и только том случае, если при данном состоянии дерева решений на концах других ветвей не существует верхних границ, превосходящих значение рекорда.
В данном случае критерий не выполняется, так как 153,75 больше 144.
- Ветвление следует продолжить по подзадаче № 1.1, которая дает наибольшую на данный момент верхнюю границу из подзадач, находящихся на концах ветвей. В качестве основы для ветвления выбирается дробное значение переменной х2 = 4,75.
Так как 4 < x1=4,75 < 5 то
задача 1.1.1. → задача 1.1.2.
2x1+x2≤9 → 2x1+x2≤9
5x1+4x2≤29 → 5x1+4x2≤29
х2<=4 → х2>=5
х1<=2 → х1<=2
х1>=0, х2>=0х1>=0, х2>=0
F=27x1+21x2 → max → F=27x1+21x2 → max
При решении подзадачи 1.1.1. в Excel добавим ограничение х2<=4
В результате получим:
х1=2, х2=4, Fмах=138
При решении подзадачи 1.1.2. в Excel добавим ограничение х2>=5
В результате получим:
х1=1,8, х2=5, Fмах=153,6
153,6 — уточненная верхняя граница.
- Проверка оптимальности текущего целочисленного рекорда после очередного ветвленияпоказывает, что критерий вновь не выполняется, так как 153,6 больше 138.
- Продолжаем ветвление по подзадаче 1. Рассмотрим подзадачу 1.3.В качестве основы для ветвления выбирается дробное значение переменной х2 =4,3.
Так как 3 < x2=4,3 < 4 то
задача 1.3. → задача 1.4.
2x1+x2≤9 → 2x1+x2≤9
5x1+4x2≤29 → 5x1+4x2≤29
х2<=4 → х2>=5
х1>=0, х2>=0х1>=0, х2>=0
F=27x1+21x2 → max → F=27x1+21x2→ max
При решении подзадачи 1.3. в Excel добавим ограничение х2<=4
В результате получим:
х1=2,5, х2=4, Fмах=151,5
При решении подзадачи 1.4. в Excel добавим ограничение х2>=5
В результате получим:
х1=1,8, х2=5, Fмах=153,6
- Продолжим ветвление по подзадаче 1.4.
В качестве основы для ветвления выбирается дробное значение переменной х1 = 1,8.
Так как 1 < x1=1,8 < 2, то задача 1.4.1. → задача 1.4.2.
2x1+x2≤9 → 2x1+x2≤9
5x1+4x2≤29 → 5x1+4x2≤29
х2>=5 х2>=2
х1<=1 х1<=2
х1>=0, х2>=0 → х1>=0, х2>=0
F=27x1+21x2 →max → F=27x1+21x2 → max
При решении подзадачи 1.4.2. — поиск не может найти подходящего решения.
При решении подзадачи 1.4.1. в Excel добавим ограничение х2<=1.
В результате получим: х1=1, х2=6, Fмах=153
Таким образом, значение 153 является новым текущим целочисленным рекордом, отменяющим прежний рекорд 144.
Оптимальным решением этой задачи будет Fмах=153, при х1=1, х2=6.
Следует отметить, что никаким округлением решения вспомогательной задачи № 1 (х1=2,3, х2=4,3) в принципе невозможно получить оптимальное решение х1=1, х2=6.
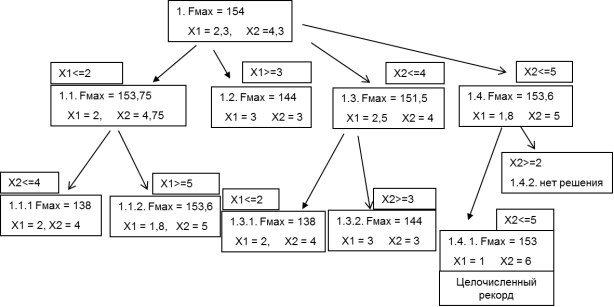
Рис. 1. Алгоритм «метода ветвей и границ» Дерево решений
Литература:
- Гармаш А. Н., Орлова И. В. Математические методы в управлении: Учебное пособие. — М.: Вузовский учебник: ИНФРА-М, 2014. — 272 — c.
- Математическое моделирование экономических процессов в сельском хозяйстве / Гатаулин А. М., Гаврилов Г. В., Сорокина Т. М. и др.; Под ред. А. М. Гатаулина. — СПБ.: ООО «ИТК ГРАНИТ», 2009. — 432 с.
- Савиных В. Н. Математическое моделирование производственного и финансового менеджмента [Текст]: учеб. пособие / В. Н. Савиных. — Новосибирск: СГГА, 2007. — 219 с.
- Алексеев Г. В. Численное экономико-математическое моделирование и оптимизация [Электронный ресурс]: учебное пособие / Алексеев Г. В., Холявин И. И.— С.: Вузовское образование, 2013. 195— c. — Режим доступа: http://www.iprbookshop.ru/16905. — ЭБС «IPRbooks».







