Хроматические номера прямоугольников



Данная работа посвящена исследованию хроматических номеров и нахождению минимальных раскрасок. Похожая тема была представлена на Колмогоровских чтениях в 2005 году. Тогда в совместной работе Веры и Елены Бушмановых были найдены хроматические номера всех тетра- и пентамино. Задача, являющаяся частным случаем этой работы, была представлена на Санкт-Петербургской городской олимпиаде в 2010 году.

Тема хроматических номеров и минимальных раскрасок породила много открытых вопросов, большинство из которых не решены до сих пор. В частности, оказалось, что даже нахождение хроматических номеров прямоугольников представляет собой весьма сложную и содержательную задачу. В данной работе найдены хроматические номера «широких» прямоугольников, т. е. тех, у которых отношение большей стороны к меньшей не превосходит двух.

Постановка и решение задачи

Определение: Рассмотрим бесконечную клетчатую плоскость, раскрашенную в k цветов, и клетчатую фигурку (полимино) X. Раскраску будем считать правильной, если она обладает следующим свойством: как бы мы ни расположили данную фигуру X на плоскости (по клеточкам), цвета клеток, которые ограничены фигурой X, будут различными. Наименьшее такое k будем называть хроматическим номером фигуры X (обозначаем cr(X)), а соответствующую раскраску назовём минимальной.

Лемма 1: Если фигура X содержится в фигуре Y, то cr(X)cr(Y)

Доказательство: (Бушмановы) Возьмем минимальную, подходящую для Y раскраску. Допустим, что эта раскраска не подходит для фигурки X. Значит, есть какая-то фигурка, X не покрашенная в разные цвета, но этой фигурке соответствует фигурка Y, которую можно наложить на фигурку X, тогда получается, что эта фигурка Y покрашена не в разные цвета. Это противоречит тому, что мы взяли подходящую для Y раскраску.

Замечание: Хроматический номер прямоугольника не меньше количества клеток в прямоугольнике, т. е. .

Следующая теорема отвечает на вопрос, в каких случаях вышеупомянутое неравенство обращается в равенство.

Теорема 1: Хроматический номер прямоугольника (где m и n — стороны прямоугольника) имеют те и только те прямоугольники, у которых одна из сторон кратна другой.

Доказательство: (Карашевич) Пусть дан прямоугольник вида . Покажем, что для него существует раскраска. Заметим, что все цвета равноправны. Пусть каждой краске соответствует число, тогда произвольно заполним прямоугольник числами от. Теперь разобьём наш прямоугольник на квадратов , пронумеруем квадраты числами от , затем ответим на вопрос задачи для полоски (см. рис. 1), теперь в пронумерованные квадраты вставим числа соответствующие номеру квадрата (см. пример на рис. 2 и рис. 3, где ). Получилась нужная раскраска.

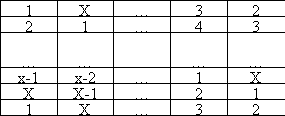
Рис. 1

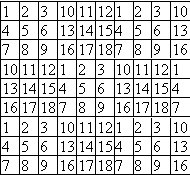
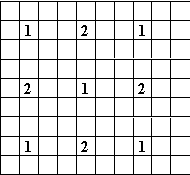
Рис. 2 Рис. 3

Если же прямоугольник имеет другой вид то для него раскраски не существует. Пусть большая сторона лежит по вертикали, тогда, нумеруя краски числами по строкам, получим, что все числа в -ом столбце кратны . Сдвинув наш прямоугольник вправо на одну клетку, легко понять, что все числа из первого столбца совпадают со всеми числами из нового (последнего) столбца. Построим новый прямоугольник, совпадающий левым верхним углом с первым прямоугольником, большая сторона которого лежит по горизонтали. Заметим, что в этом прямоугольнике в каждом -ом столбце содержаться числа кратные r, но так как по горизонтали таких чисел , а в первом прямоугольнике значит, раскраска некорректна (см. рис. 4).

Рис. 4

Теорема 2: Если в прямоугольнике отношение большей стороны к меньшей меньше , но больше , то хроматический номер данной фигуры равен ², где — длина меньшей стороны, т.e. если , то

Доказательство: Разобьем наш прямоугольник на блоки, как показано на рис. 5 (жирными линиями выделен исходный прямоугольник):

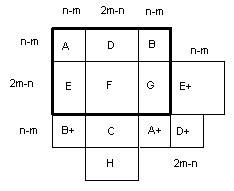
Рис.5

В данном случае мы просто переворачиваем наш прямоугольник четыре раза и полученные части выделяем в блоки. Блоки А, В, Е, D, F, G — образуют изначальный прямоугольник. Рассмотрим прямоугольник С, все цвета в этом блоке не совпадают с цветами исходного прямоугольника. Теперь рассмотрим прямоугольник А+. Он не может иметь общих цветов с прямоугольниками D, B, E, F, G, C. Из этого следует, что в прямоугольнике А+ могут быть только цвета из блока А либо новые цвета. Также рассмотрим прямоугольник В+. Он не может иметь общих цветов с прямоугольниками A, D, E, F, G, C. Аналогично в В+ должны быть цвета из В либо новые. Теперь посмотрим на самый правый блок — это блок Е, с возможно какими-то новыми цветами. Под ним будет располагаться блок D (с возможно какими-то новыми цветами). И наконец, рассмотрим блок, находящийся под блоком С и по размерам равный блоку F. В нем (с учетом уже прибавленных) в сумме новых цветов будет столько же, сколько и в блоке F. Теперь мы можем считать, что у нас появился новый блок (назовем его Н), по размерам равный блоку F.

Теперь посчитаем, сколько всего цветов у нас затрачено:

+ +

Получили, что у нашего прямоугольника хроматический номер не менее чем у прямоугольника . Исходный же прямоугольник помещается в прямоугольник . По лемме хроматический номер меньшего прямоугольника не больше хроматического номера большего прямоугольника. Из этого следует, что cr(n, m) строго равен хроматическому номеру прямоугольника . По теореме 1 хроматический номер в точности равен . На данной картинке мы использовали, что блок Е+ «длиннее», чем блок D, т. е. В противоположном случае утверждение про блок Н неверно. Таким образом, теорема верна при условии

. Доказано.

Все раскраски, возникающие в работе, построены по следующему принципу. Дана координатная плоскость (точки с целочисленными координатами соответствуют центрам клеток). Покрасим клетку (0,0) в первый цвет. Возьмем два вектора а = (x1,y1) и b = (x2, y2). Покрасим клетки в этот же цвет, где k, l — целые числа. Остальные цвета покрасим сдвигом на вектор относительно первого цвета. Количество цветов в этой раскраске равно площади параллелограмма, образованного векторами .

Лемма 2: площадь параллелограмма, образованного двумя векторами (x1,y1) и (x2,y2) равна |x2y1 — x1y2|.

Доказательство: Рассмотрим параллелограмм (см. рис. 6), образованный двумя векторами (x1,y1) и (x2,y2): Sпараллелограмма = (x1+x2)(y1+y2) — x1y2 — x1y2 — x2y2 — x1y1 = = x1y1 + x2y1 + x1y2 + x2y2 — x1y2 — -x1y2 — x2y2 — x1y1 = x2y1 — x1y2 Что и требовалось доказать.

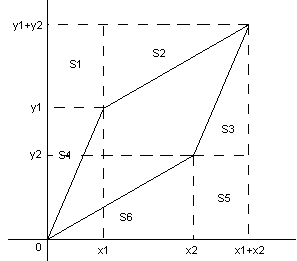
Рис. 6

Теорема 3: Если в прямоугольнике отношение большей стороны к меньшей меньше 3/2, но больше 1, то хроматический номер данной фигуры равен , где — длина большей стороны, а — длина меньшей, то есть если , то .

Доказательство:Найдем такие целые , что . Буквами A, B, C, D, E, F обозначим наборы различных цветов, которые должны быть в искомой раскраске (см. рис.7).

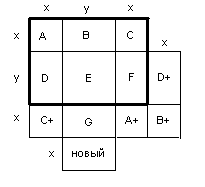
Рис.7

Повернём исходный прямоугольник на 90 градусов относительно левого верхнего угла. В квадрате C+ могут быть только цвета С или новые (их мы обозначаем как +) Аналогично выясняем для прямоугольника A+. Вследствие этих двух поворотов в прямоугольнике G новый цвет, который мы обозначимc как G. В прямоугольнике D+ может быть либо цвет D, либо новый. В прямоугольнике E+ может быть либо цвет E, либо новый. Теперь рассмотрим самый нижний прямоугольник.

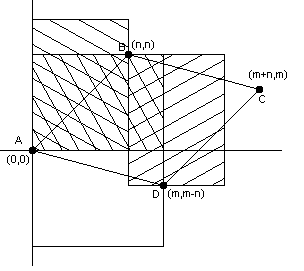
Рис.8

В нем может быть только новый цвет и цвета, которые есть в В, но нет в В+.

Получается, что кол-во цветов, нужных для раскраски плоскости не менее

=

Из того что следует, что ,

=

Докажем, что их достаточно. Рассмотрим координатную плоскость. Покрасим целые точки цветами. Пусть в точках A(0,0), B(n,n), C(m+n,m), D(m,m-n) находится цвет G (см. рис. 8). Заметим, что на плоскости не существует прямоугольников , содержащих два цвета G. Тогда кол-во различных цветов равно площади параллелограмма ABCD. . Что и требовалось доказать.

Итог

В данной работе найдены хроматические номера «широких» прямоугольников, т. е. тех, у которых отношение большей стороны к меньшей не превосходит двух. Задача разбивается на два случая. Если в прямоугольнике отношение большей стороны к меньшей меньше 2, но больше 3/2, то хроматический номер данной фигуры равен , где — длина меньшей стороны. Для прямоугольников, у которых отношение большей стороны к меньшей меньше 3/2, но больше 1, хроматический номер равен , где — длина большей стороны, а — длина меньшей.