Нахождение минимального остовного дерева — задача, которую решили уже давно и даже несколькими методами. Однако, на мой взгляд, реализация таких, проверенных временем алгоритмов позволяет глубже разобраться в проблеме и получить неоценимый опыт.
Для изучения данной задачи был выбран алгоритм Борувки, изобретенный еще в 1926 году. Первоначально предполагалось написать программу, которой на вход подавался граф, а на выходе получалось остовное дерево.
Однако в ходе реализации стало ясно, что тестировать ее не на чем. И надо сказать, что проблема входных данных достаточно часто встает при написании любых алгоритмов, поэтому было предложено написать алгоритм-программу, которая генерировала такие графы, которые бы максимально усложняли нахождение минимального остовного дерева для алгоритма Борувки.
Первоначальная идея была в том, чтобы создать алгоритм, который бы генерировал граф по количеству вершин и коэффициенту кластерности. Сначала выберем в сети некоторую вершину ![]() , имеющую
, имеющую ![]() ребер. Если первые ближние соседи этой вершины являются частью клики, между ними существует
ребер. Если первые ближние соседи этой вершины являются частью клики, между ними существует ![]() ребер. Отношение между числом
ребер. Отношение между числом ![]() ребер, действительно существующих между
ребер, действительно существующих между ![]() вершинами, и общим числом ребер
вершинами, и общим числом ребер ![]() является значением коэффициента кластерности вершины
является значением коэффициента кластерности вершины ![]() . Путем изменения этого коэффициента можно было бы генерировать совершенно разные графы. И опытном путем можно было определить наиболее замедляющий алгоритм коэффициент. Из графа затравки выращивался граф большего размера, на котором количество транзитивно замкнутых вершин увеличивалось ровно настолько, чтобы обеспечить нужный коэффициент кластерности.
. Путем изменения этого коэффициента можно было бы генерировать совершенно разные графы. И опытном путем можно было определить наиболее замедляющий алгоритм коэффициент. Из графа затравки выращивался граф большего размера, на котором количество транзитивно замкнутых вершин увеличивалось ровно настолько, чтобы обеспечить нужный коэффициент кластерности.
Но от этой идеи пришлось отказаться в связи с неоправданно высокой сложностью данного способа генерации. Даже на ранних этапах, просто для того, чтобы выяснить кластерность выращенного графа приходилось тратить слишком много времени.
Значит был нужен алгоритм проще, который обладал бы нужными свойствами для замедления Борувки. Была предложена следующая идея: создавать графы, в которых сильно связные компоненты объединялись небольшим количеством ребер. Почему данный вариант должен был сработать? Достаточно рассмотреть устройство алгоритма Борувки.
Пусть ![]() подграф графа
подграф графа ![]() . Изначально
. Изначально ![]() содержит все вершины из
содержит все вершины из ![]() и не содержит ребер. Будем добавлять в
и не содержит ребер. Будем добавлять в ![]() ребра следующим образом: пока
ребра следующим образом: пока ![]() не является деревом:
не является деревом:
- Для каждой компоненты связности находим минимальное по весу ребро, которое связывает вершину из данной компоненты с вершиной, не принадлежащей данной компоненте.
-
Добавим в
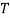 все ребра, которые хотя бы для одной компоненты связности оказались минимальными. Получившийся граф
все ребра, которые хотя бы для одной компоненты связности оказались минимальными. Получившийся граф 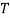 является минимальным остовным деревом графа
является минимальным остовным деревом графа 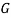 .
.
Данный алгоритм может работать неправильно, если в графе есть ребра равные по весу. Например, полный граф из трех вершин, вес каждого ребра равен один. В ![]() могут быть добавлены все три ребра. Избежать эту проблему можно, выбирая в первом пункте среди ребер, равных по весу, ребро с наименьшим номером.
могут быть добавлены все три ребра. Избежать эту проблему можно, выбирая в первом пункте среди ребер, равных по весу, ребро с наименьшим номером.
Количество компонент связности растет тем медленней, чем больше компонент на шаге выбирают одновременное связывание. Предложенная модель графа хороша именно этим: высокие показатели связности кластеров обеспечивают довольно большое количество одновременных связываний, в то же время не давая выйти за их пределы.
Осталось понять, как строить такой граф. Решение нашлось довольно быстро. Так как граф состоит из кластеров, то в первую очередь нужно создать их множество, а после соединить небольшим количеством ребер. Замечу, что внешние ребра должны весить больше, чем внутренние, так как тогда связывание не будет выходить за пределы единого кластера.
Реализация.
Дело оставалось за малым: реализовать это. Первым делом стоило продумать архитектуру. Граф, конечно же, нужно было хранить в списке смежности, так как эта структура сочетает в себе быстроту, небольшое количество используемой памяти, удобство. Список состоит из вершин и дуг, им принадлежащим, следовательно, стоило создать отдельную структуру для дуги и вершины. Первая, очевидно, состоит из веса и одного из концов (так как дуга всегда принадлежит вершине). Вершина включает в себя ее название и список дуг. Ну и, самое большое, граф — состоит из списка вершин. Нужно было создать два основных метода: метод, который будет создавать кластеры, и метод, который будет их объединять.
Создание кластера.
Существуют простые схемы создания графов, которые достаточно сильно связаны. Однако, все они обладают одним недостатком: количество выделяемой памяти неизвестно. То есть приходится использовать динамические структуры данных, что не плохо, однако велик шанс занять лишнюю память. Поэтому было решено использовать схему, в которой количество дуг для каждой вершины определяется заранее случайным образом. Таким образом, был необходим метод, которому на вход подавалось количество вершин, а на выход шел бы массив, каждый элемент которого соответствовал степеням вершин. Далее нужно было заполнить граф дугами так, чтобы он был связным.
Массив степеней вершин.
Очевидно, что для массива степеней вершин подойдет не любая последовательность натуральных чисел, на нее налагается несколько условий, а точнее должна выполняться теорема Эрдёша-Галлаи. Теорема Эрдёша-Галлаи (критерий Эрдёша-Галлаи) — утверждение в теории графов, задающее условие, при котором конечной последовательности натуральных чисел можно сопоставить степени вершин некоторого графа. Для формулировки утверждения вводятся следующие определения:
Определение:Правильная последовательность — последовательность натуральных чисел длины ![]() удовлетворяющая следующим условиям:
удовлетворяющая следующим условиям:
-
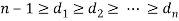
-
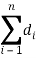 — чётное число.
— чётное число.
Определение:Графическая последовательность чисел — последовательность ![]() целых неотрицательных чисел такая, что существует граф, последовательность степеней вершин которого совпадает с ней.
целых неотрицательных чисел такая, что существует граф, последовательность степеней вершин которого совпадает с ней.
Теорема утверждает, что правильная последовательность ![]() является графической тогда и только тогда, когда для каждого
является графической тогда и только тогда, когда для каждого ![]() ,
, ![]() , верно неравенство:
, верно неравенство:
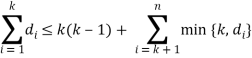
Таким образом, алгоритм создания массива степеней вершин был такой: создается массив случайных величин, который изменяется так, чтобы теорема Эрдёша-Галлаи для него выполнялась. Изменение состояло в следующем:
- Для каждого члена уже отсортированного массива проверялось неравенство Эрдёша-Галлаи.
- При его невыполнении необходимая разница (для того, чтобы неравенство стало верным) прибавлялась к правой части, либо отнималась от левой. Причем так, чтобы последовательность оставалась невозрастающей. Замечу, что это оставляет неравенство верным для уже проверенных вершин, так как левая часть всегда только уменьшается, а правая только увеличивается. На выходе получается верный массив.
Заполнение графа дугами.
Заполнение идет по схеме: наибольшее — наименьшему, то есть мы идем с начала массива и каждую вершину связываем с вершинами с наименьшей степенью (если они уже не соединены). Получившийся граф с большой степенью вероятности будет связным. Это звучит весьма опасно, но практически всегда работает (о случаях, когда это не так, я расскажу далее). То есть на выходе мы получаем хорошо связный кластер.
Связывание кластеров.
В этой части нет никаких сложностей. Граф постепенно наращивается путем присоединения кластеров к уже существующей части. При этом количество дуг – случайно, их вес больше чем вес дуг кластеров. Существует возможность регулировать размер кластеров.
Проблемы иих возможные решения.
Описанный выше алгоритм генерации работает относительно стабильно, однако требует доработки. В частности, добавление дуг в кластер не гарантирует его связности. Уже были замечены случаи, когда на маленьких кластерах (<20) наблюдались патологии в виде 2 вершин, который были связаны только друг с другом. Однако, маленькие кластеры не замедляют алгоритм, а поэтому пользоваться ими при тестах не нужно. Обеспечить связность графа можно подумав над критерием Гавели-Хакими, который позволяет строить простые графы из графической последовательности.
Другая важная проблема — память. При кластерах размера десяти тысяч вершин ее хватает только на сорок тысяч, при размере около пяти – на сто тысяч. То есть необходимо рассчитывать максимальный размер кластера при заданном размере. Самым лучшим способом увеличить размер генерируемого графа и размеры его кластеров будет использование не оперативной, а обычной памяти. Но, к сожалению, за это придется платить скоростью работы программы.
Литература:
- neerc.ifmo. Алгоритм Борувки // ИТМО. –– 2015. –– URL: http://neerc.ifmo.ru/wiki/index.php?title=Algorithm_Boruvki
- Wikipedia. Теорема Эрдеша-Галлаи // Википедия, свободная энциклопедия. –– 2015. –– URL: https://ru.wikipedia.org/wiki/Theorem_Erdesh_Galai
- Критерий Гавела-Хакими. –– 2015. –– URL: http://pco.iis.nsk.su/grapp2/html/ReqtypetNamekriteri2_gavela_-_hakimi.html







