В статье предложен авторский вариант декомпозиции линейной системы обыкновенных дифференциальных уравнений, описывающей динамику квадрокоптера, упрощающий последующий анализ модели и синтез системы управления. Данный подход позволяет преобразовать сложную MIMO-систему в 6 независимых SISO-подсистем.
Ключевые слова: квадрокоптер, системы управления, декомпозиция, пространство состояний
В настоящее время сфера применения беспилотных летательных аппаратов (далее БПЛА) в жизнедеятельности человека неуклонно расширяется. Так, ни одна современная военная операция не происходит без предварительной разведки с применением БПЛА. Крупные интернет-магазины уже используют дронов-курьеров в штатном режиме. Обыкновенному же пользователю БПЛА могут предложить возможность проведения качественной фото- или видеосъемки любого события по вполне приемлемым ценам. В данной статье будет рассмотрена математическая модель БПЛА с четырьмя несущими винтами, вращающимися в диагонально противоположных направлениях. Данная математическая модель основана на системе обыкновенных дифференциальных уравнений, которая получена путем линеаризации системы, выведенной в [1]. Так как синтез системы управления и анализ модели значительно упрощается при работе с SISO-системами (Single-Input Single-Output), по сравнению с MIMO-системами (Multiple-Input Multiple-Output), работа посвящена декомпозиции линейной MIMO-системы на несколько SISO-подсистем.
Основным объектом данной работы является система обыкновенных дифференциальных уравнений, полученная из модели динамики квадрокоптера вида (1), представленной в [1], путем линеаризации в окрестности положения равновесия (2).
.(1)
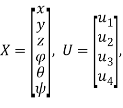
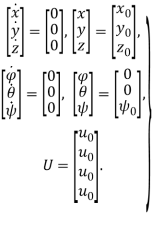(2)
Где управляющий сигнал 
представляет собой квадрат угловой скорости винта i-го мотора квадрокоптера, 
— координаты центра масс квадрокоптера в абсолютной системе координат, 
— углы Эйлера, представляющие собой ориентацию квадрокоптера (крен, тангаж и рысканье соответственно). Значение 
находится из уравнения вертикальной динамики квадрокоптера с допущением, что при данной величине управляющего сигнала БПЛА висит в воздухе неподвижно (по оси 
) в горизонтальном положении:
Таким образом, значение управляющего сигнала
определяется как
где 
— масса квадрокоптера, 
— сила тяжести и 
— коэффициент тяги моторов. Подробнее с исходной нелинейной моделью квадрокоптера (а так же с ее выводом) вы можете ознакомиться в [1].
Для линеаризации системы разложим правую часть системы в отклонениях от положения равновесия в ряд Тейлора как функцию нескольких переменных и отбросим нелинейные слагаемые. В результате получим следующую систему ОДУ:
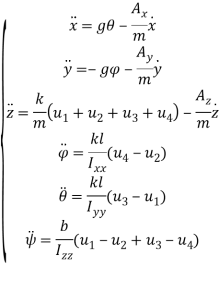,(3)
где 
— коэффициенты аэродинамического сопротивления, l — расстояние от центра масс квадрокоптера до моторов, 
— моменты инерции, 
— коэффициент крутящего момента моторов.
Переходя от линейной системы (3) к системе в пространстве состояний (4), получим модель квадрокоптера с 4 входами (управляющие сигналы для каждого из моторов) и 6 выходами-измерениями.
(4)
,
.
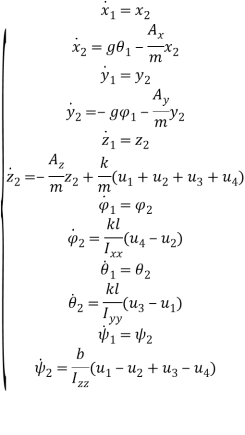
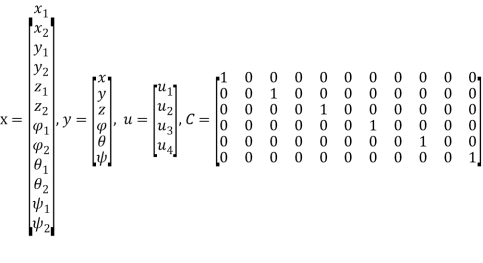Передаточная матрица системы в данном случае будет иметь размерность
, что, несомненно, вызывает определенные сложности при дальнейшей работе с моделью. Наложив некоторые ограничения на вид управляющего сигнала, можно разделить MIMO-систему на SISO-подсистемы, работать с которыми определенно проще.
Предположим, что квадрокоптер неподвижно весит в воздухе. Величина управляющего сигнала в данном случае одинакова для каждого мотора и равняется, как было выяснено ранее, . Как видно из (3), чтобы, не потеряв горизонтального положения (
), изменить лишь высоту, необходимо изменить управляющий сигнал для каждого мотора на одинаковую величину (обозначим 
). Если же поставлена задача изменить лишь угол крена 
, то достаточно изменить 
и 
на одинаковую величину 
с разным знаком. Аналогичная ситуация и с углом тангажа 
— необходимо изменить на одинаковую величину 
с разным знаком управляющие сигналы для первого и третьего моторов. Для управления углом рысканья 
будем изменять мощности моторов на одинаковую величину 
в разную сторону, если они находятся на разных осях квадрокоптера. Таким образом, замена для вектора 
будет иметь вид:
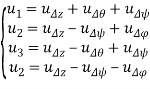.(5)
Подставив (5) в систему (3), получим в результате:
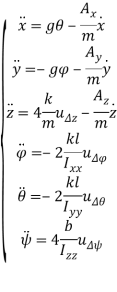(6)
Рассмотрим теперь систему (6). Как можно заметить, при переходе к модели в пространстве состояний, возможна её декомпозиция на 6 SISO-подсистем:
, 
,
,
.
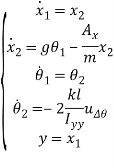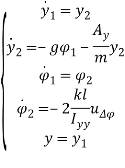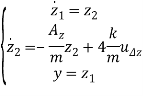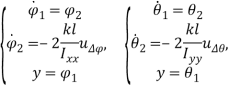
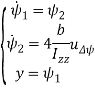Данные системы значительно удобнее использовать при работе с передаточными функциями, например, частотном анализе. Также, основываясь на вышеизложенных результатах, можно построить LQR-регулятор (с использованием асимптотических наблюдателей), который, к тому же, достаточно просто проверить на робастность.
Литература:
- Luukkonen T., Modelling and control of quadcopter, 2011, P.2–6.
