В работе в пространстве ![]() -функций, заданных на сфере
-функций, заданных на сфере ![]() и обладающих квадратично суммируемыми обобщенными производными порядка
и обладающих квадратично суммируемыми обобщенными производными порядка ![]() , вычислены нормы функционала погрешности весовой кубатурной формулы с производными. А также исследовано выражение нормы функционала погрешности для двухмерной единичной сфере.
, вычислены нормы функционала погрешности весовой кубатурной формулы с производными. А также исследовано выражение нормы функционала погрешности для двухмерной единичной сфере.
In the work in the space ![]() of functions given on sphere
of functions given on sphere ![]() and possessing square integrable generalized derivatives of
and possessing square integrable generalized derivatives of ![]() -th order the norm of the error functional of weight cubature formulas with derivative is calculated. Futhermore, the expression of the norm of the error functional on two dimensional unique sphere is investigated.
-th order the norm of the error functional of weight cubature formulas with derivative is calculated. Futhermore, the expression of the norm of the error functional on two dimensional unique sphere is investigated.
Пусть функции ![]() , заданные на единичной сфере S принадлежат некоторому Банаховому пространству B, вложенному в пространство
, заданные на единичной сфере S принадлежат некоторому Банаховому пространству B, вложенному в пространство ![]() непрерывных функций на S. Функции
непрерывных функций на S. Функции ![]()
![]() продолжим на все пространство
продолжим на все пространство ![]() , считая их постоянными на лучах, выходящих из центра сферы S и будем обозначать через
, считая их постоянными на лучах, выходящих из центра сферы S и будем обозначать через ![]() .
.
Рассмотрим погрешность кубатурной формулы
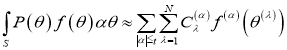 ,(1)
,(1)
на функциях из B:
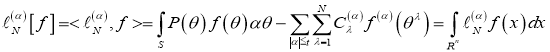 , (2)
, (2)
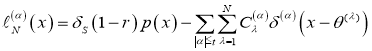 ,
,
![]() ,
, ![]() — дельта функции Дирака,
— дельта функции Дирака, ![]() ,
,
нулевой коэффициент Фурье ![]() .
.
Функция ![]() для которой имеется место равенство
для которой имеется место равенство
![]() ,
,
называется экстремальной функцией.
Погрешность (2) кубатурной формулы (1), очевидно, является функционалом, заданном на ![]() в силу предположения вложенности
в силу предположения вложенности ![]() [1], этот функционал
[1], этот функционал ![]() будет непрерывным. Поэтому он и его норма определяется по формуле [3]
будет непрерывным. Поэтому он и его норма определяется по формуле [3]
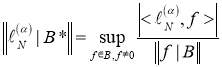 .
.
Функция ![]() для которой имеется место равенство
для которой имеется место равенство
![]() ,
,
называется экстремальной функцией.
Таким образом, задача оценки погрешности кубатурной формулы на функциях некоторого пространства ![]() , равносильна вычислению значения нормы функционала погрешности в сопряжённом к
, равносильна вычислению значения нормы функционала погрешности в сопряжённом к ![]() пространстве
пространстве ![]() или что тоже самое, нахождению экстремальной функции для данной кубатурной формулы. Для решения этой задачи в качестве
или что тоже самое, нахождению экстремальной функции для данной кубатурной формулы. Для решения этой задачи в качестве ![]() возьмём пространство
возьмём пространство ![]() — функций заданных на
— функций заданных на ![]() и обладающих квадратично суммируемыми обобщёнными производными порядка
и обладающих квадратично суммируемыми обобщёнными производными порядка ![]() , норма которых определяется равенством
, норма которых определяется равенством
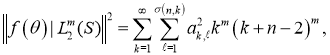 (3)
(3)
и предположим, что ![]() .
.
Справедлива следующая
Теорема. Норма функционала погрешности ![]() кубатурной формулы (1) над пространством
кубатурной формулы (1) над пространством ![]() равна
равна
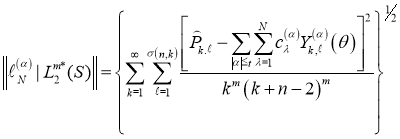 ,
,
где ![]() .
.
На основании этой теоремы, функционал погрешности кубатурной формулы (1) для функций класса ![]() имеет оценку:
имеет оценку:
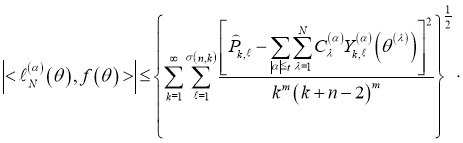
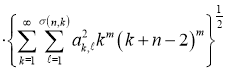 .
.
Литература:
- Соболев. С. Л. Введение в теорию кубатурных формул. М.:Наука, 1974. 808 с.
- Соболев С. Л. Некоторые применения функционального анализа в математической физике. Л.: Наука, 1950.
- Люстерник Л. А., Соболев В. И. Элементы функционального анализа. М., Наука, 1965
-
Салихов Г. Н. Оценка погрешности кубатурных формул в пространстве
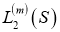 . ДАН СССР, 1975 т. 223, № 6, 1318–1321.
. ДАН СССР, 1975 т. 223, № 6, 1318–1321.
- Freeden W. An application of summation formula to numerical computation of integrals over the sphere.-Computing, 1980, v.23. № 2, p.131–146.







