Одним из классических методов изучения спектра линейного оператора ![]() в гильбертовом пространстве
в гильбертовом пространстве ![]() с областью определения
с областью определения ![]() является изучение его числового образа:
является изучение его числового образа: ![]() .
.
Пусть ![]() и
и ![]() — множества всех целых, вещественных и комплексных чисел, соответственно. Известно, что точечный спектр
— множества всех целых, вещественных и комплексных чисел, соответственно. Известно, что точечный спектр ![]() оператора
оператора ![]() лежит в
лежит в ![]() , а его аппроксимативно точечный спектр
, а его аппроксимативно точечный спектр ![]() содержится в
содержится в ![]() . Если
. Если ![]() есть замкнутый оператор и всякая компонента множества
есть замкнутый оператор и всякая компонента множества ![]() содержит хотя бы одну точку резольвентного множества
содержит хотя бы одну точку резольвентного множества ![]() оператора
оператора ![]() , то имеет место включение
, то имеет место включение ![]() . В силу теоремы Тёплица–Хаусдорфа [1] числовой образ является выпуклым подмножеством множества
. В силу теоремы Тёплица–Хаусдорфа [1] числовой образ является выпуклым подмножеством множества ![]() . С одной стороны, свойство выпуклости является важным свойством, однако надо отметить, что если спектр состоит из объединения двух непересекающихся множеств, то числовой образ не всегда дает достаточно хорошую структуру.
. С одной стороны, свойство выпуклости является важным свойством, однако надо отметить, что если спектр состоит из объединения двух непересекающихся множеств, то числовой образ не всегда дает достаточно хорошую структуру.
Для того, чтобы получить более точную информацию о спектре в вышеуказанных случаях, в работе [2] введено понятие квадратичного числового образа, изучению которого также посвящены работы [3–6]. Квадратичный числовой образ определен, если дано разложение ![]() и
и ![]() , где
, где ![]() и
и ![]() гильбертово пространство, а
гильбертово пространство, а ![]() пространство линейных ограниченных операторов в гильбертовом пространстве
пространство линейных ограниченных операторов в гильбертовом пространстве ![]() . Тогда оператор
. Тогда оператор ![]() всегда записывается в виде блочно–операторной матрицы
всегда записывается в виде блочно–операторной матрицы
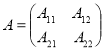 (1)
(1)
с линейными ограниченными операторами ![]() ,
, ![]() . Для неограниченного линейного оператора
. Для неограниченного линейного оператора ![]() в
в ![]() , его область определения
, его область определения ![]() необязательно должна быть разлагаемой как прямая сумма
необязательно должна быть разлагаемой как прямая сумма ![]() подпространств
подпространств ![]() ,
, ![]() и следовательно, утверждение о том, что оператор
и следовательно, утверждение о том, что оператор ![]() имеет представление (1) является дополнительным предположением. В этом случае
имеет представление (1) является дополнительным предположением. В этом случае
![]() .
.
Так как в настоящей работе рассматривается случай, когда линейный оператор ![]() является ограниченным, дальнейшие понятия приводятся для ограниченных операторов, действующих в гильбертовом пространстве
является ограниченным, дальнейшие понятия приводятся для ограниченных операторов, действующих в гильбертовом пространстве ![]() .
.
Сначала дадим определение квадратичного числового образа оператора ![]() и некоторую информацию о нем (подробно см. работу [5]). Пусть
и некоторую информацию о нем (подробно см. работу [5]). Пусть ![]() и
и ![]() — скалярное произведение и норма в
— скалярное произведение и норма в ![]() ,
, ![]() , соответственно.
, соответственно.
Множество всех собственных значений матрицы
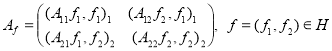
таких, что
Двум различным разложениям гильбертового пространства ![]() , могут соответствовать различные квадратичные числовые образы.
, могут соответствовать различные квадратичные числовые образы.
Например, квадратичными числовыми образами матрицы ![]()
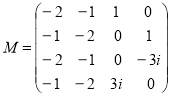 ,
,
соответствующих разложениям ![]() и
и ![]() являются различные множества [5]:
являются различные множества [5]:
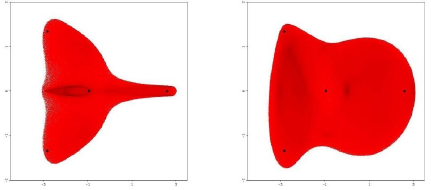
В некоторых случаях удобно воспользоваться эквивалентным описанием квадратичного числового образа, где используются ненулевые элементы ![]() и
и ![]() , необязательно имеющие нормы 1.
, необязательно имеющие нормы 1.
Для![]() ,
, ![]() положим
положим
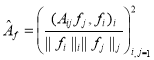
и
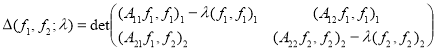 .
.
Свойство 1.Имеет место соотношение:
![]()
![]()
![]() .
.
Свойство 2.Квадратичный числовой образ всегда содержится в числовом образе:
![]() .
.
Свойство 3. Если операторная матрица ![]() имеет нижнюю или верхнюю треугольную форму, т. е.
имеет нижнюю или верхнюю треугольную форму, т. е.
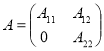 или
или 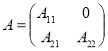 ,
,
то ![]() .
.
Аналогично числовому образу значений, квадратичный числовой образ ограниченной блочно-операторной матрицы ![]() является ограниченным подмножеством множества
является ограниченным подмножеством множества ![]() :
:
![]()
и оно замкнуто, если ![]() . В отличие от числового образа, квадратичный числовой образ, вообще говоря, невыпуклый и состоит из не более чем двух компонент. С другой стороны, квадратичный числовой образ обладает некоторыми аналогичными свойствами числового образа.
. В отличие от числового образа, квадратичный числовой образ, вообще говоря, невыпуклый и состоит из не более чем двух компонент. С другой стороны, квадратичный числовой образ обладает некоторыми аналогичными свойствами числового образа.
Литература:
- Т. Като. Теория возмущения линейных операторов. М.: Мир, 1972.
- H. Langer, C. Tretter. Spectraldecomposition of some nonselfadjoint block operator matrices. J. Operator Theory, 39:2 (1998), 339–359.
- H. Langer, A. S. Markus, V. I. Matsaev, C. Tretter. A new concept for block operator matrices: the quadratic numerical range. Linear Algebra Appl., 330:1–3 (2001), 89–112.
- H. Langer, A. S. Markus, C. Tretter. Corners of numerical ranges. In Recent advances in operator theory Groningen, 1998), vol. 124 of Oper. Theory Adv. Appl., 385–400 (Birkhauser, Basel, 2001).
- C. Tretter. Spectral Theory of Block Operator Matrices and Applications. Imperial College Press, 2008.
- C. Tretter. Spectral inclusion for unbounded block operator matrices. J. Func. Anal., 256 (2009), 3806–3829.







