Формализация гражданского процесса при английском и американском судебном правиле в виде байесовской игры



Современные методы математики нашли широкое применение в моделировании социоэкономических систем [1–27] и, в частности, моделировании гражданских процессов, где истцы подают иски в суд для получения компенсации за причинённый ответчиком вред. Существенное влияние на финансовый результат судебной тяжбы оказывает размер потенциальных судебных издержек [28], которые во многом определяется применением английского или американского правила. Все юрисдикции мира, кроме США, используют английское правило [29]. При американском правиле каждая тяжущаяся сторона сама оплачивает все свои судебные издержки вне зависимости от исхода дела. При английском правиле судебные издержки победившей стороны оплачивает сторона проигравшая. Сравнительный анализ этих правил представлен в работах [30–34]. В настоящей статье формализуется новая модель судопроизводства при английском и американском правиле в виде байесовской игры.

Байесовской игрой называется пятерка , где — множество агентов; — множество альтернатив агента ; — множество типов агента ; — функция выигрыша агента , где — декартово произведение множеств альтернатив всех агентов, — декартово произведение множеств типов всех агентов, — множество вещественных чисел; — представление агента (о типах других агентов). Каждый агент точно знает свой тип, но не знает типов других агентов. Представление агента для любого его типа задает распределение вероятностей на множестве типов других агентов, где . Если все множества конечны, то функцию можно задать как . Тогда — условная вероятность того, что типы других агентов суть соответственно , если тип агента равен . Выигрыш агента зависит от типов агентов и выбранных ими альтернатив. Если сложилась ситуация , где , а типы игроков равняются , то выигрыш агента составляет . Обозначим байесовские игры, моделирующие судопроизводственный процесс при английском правиле и американском правиле, через и соответственно.

При подаче искового заявления, истец обязан указать сумму компенсации, обозначаемую через , и в ходе судебного процесса доказать ее обоснованность. Если суд в достаточной мере согласиться с доводами истца, то ему будет присуждена требуемая сумма. Для простоты модели предполагается, что суд не может изменить сумму требуемой компенсации, а только вынести вердикт в пользу истца или ответчика. Агрегируем все судебные издержки истца в одну величину . Ответчик тратится на аналогичные издержки, обозначим их через . Пусть — вероятность истца выиграть дело по мнению истца, — вероятность истца выиграть дело по мнению ответчика.

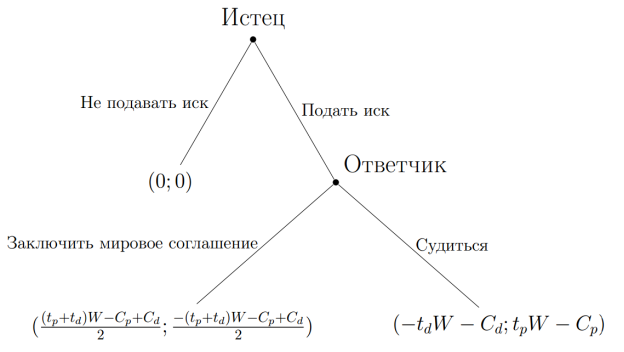
Рис. 1. Игра в позиционной форме при американском правиле

Судебный процесс может быть начат, только если истец подаст иск, т. е. заполнит исковое заявление. Разумеется, что истец может выбрать бездействие и не заполнять исковое заявление. Если истец все же подает иск, то суд отводит ответчику время на досудебное урегулирование конфликта. Ответчик может попытаться заключить мировое соглашение с истцом. Для упрощения модели предполагается, что заключение мирового соглашения бесплатно и происходит до момента траты обоих тяжущихся сторон на судебные издержки. При заключении мирового соглашения ответчик передает истцу некоторую сумму денег, а истец прекращает судебное преследование. Заключение мирового соглашения может состояться только с согласия истца и ответчика. Если истец или ответчик не согласен заключить мировое соглашение, то состоится суд, который вынесет вердикт в пользу одной из тяжущихся сторон.

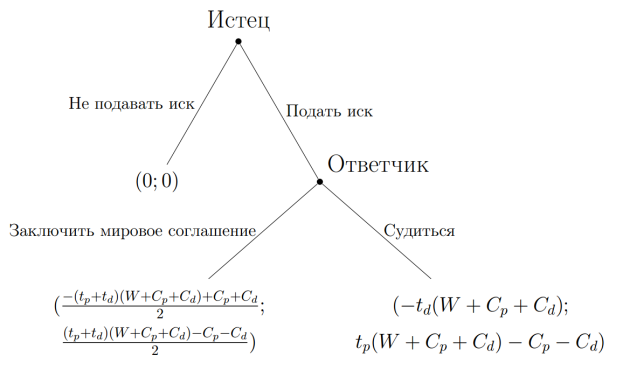
Рис. 2. Игра в позиционной форме при английском правиле

На рисунках 1 и 2 выигрыши истца и ответчика записаны в форме , где — выигрыш ответчика, а — выигрыш истца.

Формализуем игры и . В обеих играх участвуют два агента: , где первый агент — истец, а второй агент — ответчик. Истец может выбрать одну из двух альтернатив: подать иск в суд или не подавать иск в суд. Обозначим первую альтернативу через , а вторую через , тогда . Ответчик может выбрать одну из двух альтернатив: заключить мировое соглашение или судиться. Обозначим первую альтернативу через , а вторую через , тогда . Истец типа считает, что его шанс выиграть дело равен , соответственно . Ответчик типа считает, что шанс истца выиграть дело равен , соответственно . Тяжущиеся стороны не знают субъективных оценок друг друга и предполагают, что их оценки одинаковы. Соответственно и — функции тождества. Обозначим функции выигрыша истца и ответчика при английском и американском правиле через и . Если истец не подает иск в суд, то функции выигрыша истца и ответчика принимаются нулевыми. Размер компенсации истца при заключении мирового соглашения равен среднеарифметическому значению выигрыша истца и отрицательного выигрыша ответчика в случае судебного разбирательства.

Таблица 1

Функция выигрыша истца

Американское правило
Английское правило

Таблица 2

Функция выигрыша ответчика

Американское правило
Английское правило

Байесовская игра задаётся пятеркой

, а байесовская игра .

Литература:

1. Григорьева, К. В. Динамический процесс кооперативного взаимодействия в многокритериальной (многоагентной) задаче почтальона / К. В. Григорьева, О. А. Малафеев // Вестник гражданских инженеров. — Санкт-Петербург: Изд-во СПбГАСУ, 2011. — № 1. — C. 150–156.

2. Колокольцов, В. Н. Динамические конкурентные системы многоагентного взаимодействия и их асимптотическое поведение (часть I) / В. Н. Колокольцов, О. А. Малафеев // Вестник гражданских инженеров. — Санкт-Петербург: Изд-во СПбГАСУ, 2010. — № 4. — C. 144–153.

3. Колокольцов, В. Н. Динамические конкурентные системы многоагентного взаимодействия и их асимптотическое поведение (часть II) / В. Н. Колокольцов, О. А. Малафеев // Вестник гражданских инженеров. — Санкт-Петербург: Изд-во СПбГАСУ, 2011. — № 1. — C. 134–145.

4. Дроздова, И. В. Эффективность вариантов реконструкции городской жилой застройки / И. В. Дроздова, О. А. Малафеев, Л. Г. Паршина // Экономическое возрождение России. — Санкт-Петербург: Изд-во ИНИР, 2008. — № 3. — С. 63–67.

5. Малафеев, О. А. Математические модели конфликтных ситуаций и их разрешение / О. А. Малафеев, А. И. Муравьев. — Санкт-Петербург: Изд-во СПбГУЭФ, 2000. — Т. 1. — 283 с.

6. Малафеев, О. А. Математические модели конфликтных ситуаций и их разрешение / О. А. Малафеев, А. И. Муравьев. — Санкт-Петербург: Изд-во СПбГУ ЭиФ, 2001. — Т. 2. — 294 с.

7. Григорьева, К. В. Методы решения динамической многокритериальной задачи почтальона / К. В. Григорьева, О. А. Малафеев // Вестник гражданских инженеров. — Санкт-Петербург: Изд-во СПбГАСУ, 2011. — № 4. — С. 156–161.
8. Малафеев, О. А. Математическое моделирование развития компании / О. А. Малафеев, К. С. Черных // Экономическое возрождение России. — Санкт-Петербург: Изд-во ИНИР, 2004. — № 1. — С. 60–66.
9. Малафеев, О. А. Конкурентное управление в моделях аукционов / О. А. Малафеев, К. Н. Грицай // Проблемы механики и управления: Нелинейные динамические системы: сб. науч. трудов ПГНИУ. — Пермь, 2004. — № 36. — С. 74–82.
10. Ершова, Т. А. Конфликтные управления в модели вхождения в рынок / Т. А. Ершова, О. А. Малафеев // Проблемы механики и управления: Нелинейные динамические системы: сб. науч. трудов ПГНИУ. — Пермь, 2004. — № 36. — С. 19–27.
11. Малафеев, О. А. Моделирование конфликтных ситуаций в социально-экономических системах / О. А. Малафеев, А. И. Муравьев. — Санкт-Петербург: Изд-во СПбГУ ЭиФ, 1998. — Т. 2. — 317 с.
12. Малафеев, О. А. Равновесие в диффузионной конфликтной модели экономики со многими участниками / О. А. Малафеев, М. С. Троева // Вопросы механики и процессов управления. — Санкт-Петербург: Изд-во СПбГУ, 2004. — № 22. — С. 146–153.

13. Малафеев, О. А. Многоагентное взаимодействие в динамической задаче управления венчурными строительными проектами / О. А. Малафеев, О. С. Зенович, В. К. Севек // Экономическое возрождение России. — Санкт-Петербург: Изд-во ИНИР, 2012. — № 1. — С. 124–131.

14. Малафеев, О. А. Компромисс и равновесие в моделях многоагентного управления в коррупционной сети социума / О. А. Малафеев, Д. С. Бойцов, Н. Д. Рединских, Е. Г. Неверова // Молодой ученый. — Казань, 2014. — № 10 (69). — С. 14–17.

15. Колпак, Е. П. Математическая модель стачечного движения в России в начале XX века / Е. П. Колпак, А. И. Бронникова, В. Ю. Полежаев // Молодой ученый. — 2015. — № 3. — С. 4–15.

16. Колпак, Е. П. О численных методах решения эволюционных уравнений на примере математической модели «хищник-жертва» / Е. П. Колпак, И. В. Жукова, Д. С. Степанова, А. В. Крицкая // Молодой ученый. — 2014. — № 4. — С. 20–30.

17. Колпак, Е. П. Математическая модель логистической популяции на линейном ареале / Е. П. Колпак, Е. А. Горбунова, М. В. Столбовая, Ю. Е. Балыкина // Молодой ученый. — 2014. — № 3. — С. 6–14.

18. Малафеев, О. А. Динамическая нестационарная задача инвестирования проектов в условиях конкуренции / О. А. Малафеев, О. В. Пахар // Проблемы механики и управления: Нелинейные динамические системы: сб. науч. трудов ПГНИУ. — Пермь, 2009. — № 41. — С. 103–108.

19. Грицай, К. Н. Задача конкурентного управления в модели многоагентного взаимодействия аукционного типа / К. Н. Грицай, О. А. Малафеев // Проблемы механики и управления: Нелинейные динамические системы: сб. науч. трудов ПГНИУ. — Пермь, 2007. — № 39. — С. 36–45.

20. Малафеев, О. А. Устойчивость по Ляпунову и колебательность в экономических моделях: учебное пособие./ О. А. Малафеев, А. Ф. Зубова. — Санкт-Петербург: Изд-во СПбГУ, 2001. — 101 c.

21. Григорьева, К. В. Статистическая коалиционная модель инвестирования инновационных проектов / К. В. Григорьева, А. С. Иванов, О. А. Малафеев // Экономическое возрождение России. — Санкт-Петербург: Изд-во ИНИР, 2011. — № 4. — С. 90–98.

22. Гордеев, Д. A. Стохастическая модель принятия решения о выводе на рынок инновационного продукта / Д. А. Гордеев, О. А. Малафеев, Н. Д. Титова // Вестник гражданских инженеров. — Санкт-Петербург: Изд-во СПбГАСУ, 2011. — № 2. — С. 161–166.

23. Парфенов, А. П. Равновесие и компромиссное управление в сетевых моделях многоагентного взаимодействия / А. П. Парфенов, О. А. Малафеев // Проблемы механики и управления: Нелинейные динамические системы: сб. науч. трудов ПГНИУ. — Пермь, 2007. — № 39. — С. 154–167.

24. Малафеев, О. А. Устойчивость и некоторые численные методы в конфликтно управляемых системах / О. А. Малафеев, М. С. Троева. — Якутск: Изд-во ЯГУ, 1998. — 102 c.

25. Малафеев, О. А. Математическое и компьютерное моделирование социально-экономических систем на уровне многоагентного взаимодействия (введение в проблемы равновесия, устойчивости, надежности) / О. А. Малафеев, А. Ф. Зубова. — Санкт-Петербург: Мобильность-плюс, 2006. — 1006 c.

26. Малафеев, О. А. Управляемые конфликтные системы / О. А. Малафеев. — Санкт-Петербург: Изд-во СПбГУ, 2000. — 280 c.

27. Акуленкова, И. В. Проблемы реконструкции жилищно-коммунального хозяйства мегаполиса, монография / И. В. Акуленкова, Г. Д. Дроздов, О. А. Малафеев. — Санкт-Петербург: Санкт-Петербургский государственный университет сервиса и экономики, 2007. — 187 c.

28. Lewis, R. Tort personal injury claims statistics: Is there a compensation culture in the United Kingdom / Richard Lewis, Annette Morris, Ken Oliphant // Torts Law Journal. — 2006. — Vol. 14, no. 2. — P. 158–175.

29. Capisio, M. V. Awards of Attorneys Fees by Federal Courts, Federal Agencies and Selected Foreign Findings / Mary V. Capisio, Henry Cohen. — New York: Nova Publishers, 2002.

30. Gould, J. P. The economics of legal conflicts / John P. Gould // The Journal of Legal Studies. — 1973. — Vol. 2, no. 2. — P. 55–81.

31. Posner, R. A. An economic approach to legal procedure and judicial administration / Richard A. Posner // The Journal of Legal Studies. — 1973. — Vol. 2, no. 2. — P. 399–458.

32. Landes, W. M. An economic analysis of the court / William M. Landes // Journal of Law and Economics. — 1971. — Vol. 14, no. 1. — P. 61–107.

33. Bebchuk, L. A. Litigation and settlement under imperfect information / Lucian Arye Bebchuk // Rand Journal of Economics. — 1984. — Vol. 15, no. 3. — P. 404–415.

34. Schwab, C. Free choice of legal fee shifting rules? / Christian Schwab, Hin-Yue Benny Tang, Stefan Winter // European Journal of Law and Economics. — 2014. — Vol. 37, no. 2. — P. 229–324.