Одной из проблем является зашумления полезного сигнала при работе матричных фотоприемных устройств (МФПУ). Поэтому для решения данной проблемы представлены возможности подавления геометрических шумов, как на аппаратном, так и на программном уровне. Акцент сделан на борьбу с геометрическими шумами на программном уровне.
Применение данного метода и решения системы уравнений позволит выявить зашумлённый сигнал и в дальнейшем ликвидировать его, что в свою очередь позволит получать более точные измерения при работе с тепловизионной установкой.
Ключевые слова: термография, геометрический шум, термограмма
Основной проблемой является зашумления полезного сигнала при работе матричных фотоприемных устройств (МФПУ), причины которого кроются в: дискретной природе вещества, из которого сделаны фотоприемные элементы (ФПЕ) матрицы (разброс характеристик ФПЕ, далее — геометрические шумы) зернистости матрицы (битые пиксели) излучении (атомы, фотоны) тепловом движении частиц (быстрые флуктуации относительно среднего значения сигнала) [1]; недостаточной коррекции неоднородности ФПЕ сканирующей матрицы и, как следствие, нарушение точности восстановления изображений.
Традиционный подход к подавлению геометрических шумов в работе МФПУ связан с использованием эталонных излучателей, дают достаточно высокую однородность интенсивности излучения [2].
Это реализуется следующим образом: регистрируются два эталонных изображения с различными интенсивностями, по ним в линейном приближении для каждого ФПЕ исчисляются поправочные коэффициенты (мультипликативные и аддитивные), которые запоминаются в памяти вычислительного устройства и далее используются для цифровой коррекции сигналов сцены.
Сущность реализованного метода заключается во введении двумерного мало-амплитудного сканирования со специально подобранным законом, по которому матрица ФПЕ смещается относительно изображения, регистрации соответствующей последовательности кадров и их цифровая обработка [3].
С помощью детекторов ИКТ можно получить значительную информацию о слабо нагретых объектах. Так, спектральная длина волны теплового излучения человека с температурой 37 ° C составляет примерно 9,3 мкм. Детекторы ИКТ используют, как правило, длины волн, лежащие в окнах прозрачности атмосферы — в диапазоне 3–5 мкм (MIR) и 8–14 мкм (FIR) [4].
Инфракрасные камеры воспроизводят образ теплого объекта по сигналам от первичных преобразователей — датчиков теплового излучения. Выделяются два наиболее широкие классы тепловых камер: с не охлаждаемыми (UncooledFocalPlaneArray — UFPA) и охлаждаемыми (Cooled FPA) детекторами [5].
Тепловые приемники ИКТ поглощая фотоны, меняют температуру материала детектора и за счет этого — его свойства, что позволяет сгенерировать электрический сигнал. Материалы фотонных детекторов включают силицид платины PtSi, а также недорогие полупроводниковые устройства на основе материалов InSb, InAs, теллуриды кадмия и ртути HgCdTe или CdHgTe (КРТ), сульфидно-свинцовые PbS, селенидно-свинцовые PbSe и другие материалы [6] (рис. 1).
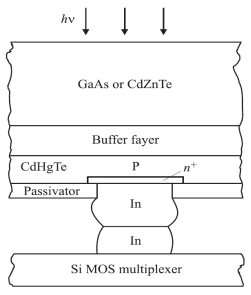
Рис. 1. Структура фоточувствительного элемента
Предлагается новый подход к подавлению геометрического шума. Сущность реализованного метода заключается во введении двумерного сканирования со специально подобранным законом, по которому матрица ФПЕ смещается относительно изображения. При смещении матрицы ФПЕ выполняется регистрация соответствующей последовательности кадров и их цифровая обработка. Идея модуляции тех или иных параметров системы (или сигнала) с целью ее идентификации уже реализовывалась другими исследователями, но, как показано в [6] и подтверждено в многочисленных экспериментах [4,5], именно двумерное сканирование позволяет решить проблему безэталонного подавления геометрического шума по сигналам сцены.
Исходным материалом является квадратная матрица ФПЕ с числом элементов в строке (столбце) 
и в линейном приближении оцифрованный сигнал 
(i, j) -го от ФПЕ:
,(1)
где
-интенсивность излучения, падающего на ФПЕ,
, 
-коэффициенты преобразования (в данной работе = 1),
- случайная составляющая сигнала (шум).
Сканирование выполняется дискретно: на пиксель вниз-вверх и пиксель вправо-влево относительно исходного положения с достаточно малыми промежутками времени.
Регистрируем полученные кадры в виде системы:
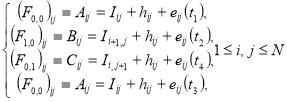(2)
где 
, 
, 
, 
— случайные величины, имеющие нулевые среднее значение.
В каждом цикле сканирования учитывается, что случайные величины , , 
, 
не коррелированны и имеют нулевые средние значения, в матрице 
и 
в течение цикла сканирования остаются неизменными.
Выполнен эксперимент, который должен предоставить все возможные данные об изменении температуры сердца на поверхности и внутри при его охлаждении до температуры проведения операции. Замеры, снятые в ходе исследования, использованы при решении системы уравнений.
Для подопытного материала было взято свиное сердце весом до 500 г, сердце находилось в пластмассовой емкости. В начале эксперимента на некоторое время было на половину погружено в теплую воду, чтобы его температура достигла примерно 25 ° С. С помощью хирургического вмешательства, выделена безымянная артерия, по которой в восходящую аорту введена полиэтиленовая канюля артериальной магистрали аппарата для региональной перфузии сердца (рис.2).
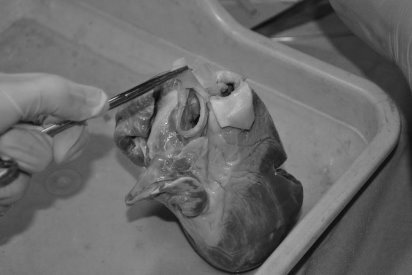
Рис. 2. Размещение полиэтиленовой канюли
Отделена восходящая аорта от общего ствола легочной артерии. Над канюлей, введенной в аорту, затянутая тесьма турникета, начато коронарную перфузию.
После подключения к выходам канюлей капельницы, начато последовательную перфузию с помощью физического раствора, который предварительно был охлажден. Для снятия температурных показателей, на сердце было произвольно выбраны 4 точки. Температурные измерения фиксировались с использованием трех приборов, а именно:
‒ ртутного термометра,
‒ цифрового термометра,
‒ тепловизора.
Постепенно температура сердца снизилась до 17оС, что соответствует его температуре при условиях осуществления хирургической операции. Для достижения такого значения температуры охлаждения сердца были использованы два флакона с физраствором для капельниц, по 500 мл каждый.
Измерения по четырем точкам фиксировались в течение времени с 14:57 до 15:34 9 раз.
Графики температур охлаждения сердца по отношению к времени представлены на рис. 3.
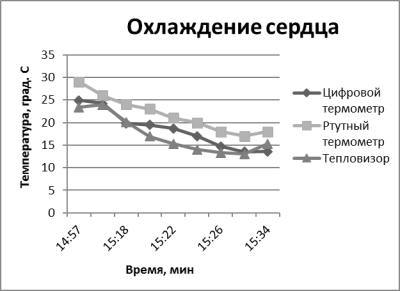
Рис. 3. Охлаждение сердца
Подставим в систему уравнений температурные данные из эксперимента, которые измерены в четырех точках на цифровой термометр и тепловизор, приведенные в таблице 1.
Таблица 1
Температурные данные
|
Время |
Цифровой термометр |
Тепловизор |
|
14:57 |
23,5 |
23,4 |
|
25,8 |
23,7 |
|
|
25,8 |
23,9 |
|
|
24,3 |
23,6 |
|
|
15:12 |
23,9 |
22,6 |
|
24,3 |
23,4 |
|
|
24 |
24 |
|
|
24,5 |
23,9 |
|
|
15:22 |
13,1 |
14 |
|
20,5 |
18,5 |
|
|
20,4 |
19,6 |
|
|
20,6 |
20 |
|
|
15:34 |
12,8 |
13,1 |
|
13,8 |
13.5 |
|
|
13,9 |
14 |
|
|
13,9 |
15 |
Имеем исходную систему, которую необходимо дополнить одним из условий нормирования:
, для фиксированного (i, j)-го ФПЕ.
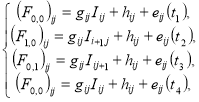
После преобразования системы уравнений имеем:
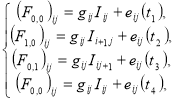
В результате решения системы уравнений, получили зашумлённый сигнал, по которому можем оценить размеры погрешности тепловизора при бесконтактном измерении температуры на поверхности сердца.
Размеры погрешности, которую дает тепловизор при измерении температуры, существенно влияет на точность получения данных о тепловой картины на поверхности измеряемого объекта, по сравнению с эталонными измерителями (цифровой термометр). В результате реализации исследования и применения к изображению данного программно-аппаратного метода устранения геометрических шумов, обнаружено случайную составляющую сигнала (шум), вызванную флуктуациями температуры приемника.
Литература:
- Сойфер В. А. Компьютерная обработка изображений. Часть 2. Методы и алгоритмы. — Соросавский образовательный журнал № 3, 1996.
- Апальков И. В., Хрящев В. В. Удаление шума из изображений на основе нелинейных алгоритмов с использованием ранговой статистики. — Ярославский государственный университет, 2007.
- Андреев А. Л. Автоматизированные телевизионные системы наблюдения. Часть II. Арифметико-логические основы и алгоритмы. Учебное пособие. — СПб: СПб, ГУИТМО, 2005. — 88с.
- Лукин А. Введение в цифровую обработку сигналов (Математические основы).- М.: МГУ, Лаборатория компьютерной графики и мультимедиа, 2002. — URL: http://pv.bstu.ru/dsp/dspcourse.pdf, http://dsp-book.narod.ru/dspcourse.djvu, http://geogin.narod.ru/arhiv/dsp/dsp4.pdf.
- Иванов Д. В. и др. Алгоритмические основы растровой графики. — Интернет университет информационных технологий. — http://www.intuit.ru/goto/course/ rastrgraph/
- Лукин С. Б. Оптико-электронные системы: Конспект лекций. ИТМО, 2004. — СПб, ИТМО ИФФ, 2004. — http://iff.ifmo.ru/kons/oes/KL.htm
