В данной статье исследуются различные механизмы выплат долгов кредиторам при банкротстве предприятия. Особый интерес представляют механизмы, использующие методы математической теории игр. Проведен обзор задачи в статическом случае и предложен новый подход, основанный на кооперативной теории динамических игр.
Ключевые слова: задача банкротства, кооперативные игры, вектор Шепли
В различной литературе понятие банкротства предприятия трактуется весьма неоднозначно, но большинство авторов под понятием «банкротство» понимают следующее:
Банкротство (нем. Bankrott, Bankarotta) — долговая несостоятельность предприятия, несостоятельность его удовлетворить требования кредиторов по оплате услуг, товаров и работ, а также неспособность вносить обязательные платежи в бюджет и внебюджетные фонды.
Успех деятельности фирмы зависит от большого числа внешних и внутренних факторов и если она ведет эту деятельность неэффективно, то настает момент, когда ее необходимо вывести с рынка. Для этого выполняется ряд процедур, одной из которых является определение ликвидационной стоимости. После чего встает вопрос о разделении этой стоимости между кредиторами, истцами и заявителями, что приводит к большому числу юридических конфликтов. Проблема заключается в том, что стоимости фирмы в большинстве случаев недостаточно, чтобы погасить все требования. Необходимо сделать оптимальное распределение денежных средств и установить соответствующие правила дележа.
Рассмотрим теперь формальную постановку задачи. Пусть у нас есть положительная величина M
- ликвидационная стоимость предприятия. Необходимо распределить её среди конечного множества агентов N (кредиторов, истцов и заявителей) вида 
, требования которых в сумме превышают число M. Определим требование i-ого агента как 
. Суммарное требование вычисляется как D =
. Обозначим класс всех задач о банкротстве 
.
Тогда под задачей банкротства будем понимать пару (d, M)
×, в которой распределяемая сумма денежных средств строго меньше суммарного требования кредиторов предприятия. Данная задача эквивалента реальной ситуации в суде по делам о банкротстве. Мы будем рассматривать конфликт претензий агентов и искать способы нахождения оптимального распределения вида (
,
,…,
). Правило дележа — это функция, которая для любой пары (d, M) ставит в соответствие вектор (,,…,) такой, что 
≤ M и выполняется неравенство 0 ≤ x ≤ d. Необходимо определить ряд таких правил и найти способы их сравнения.
Данную задачу изучают довольно длительное время. Авторы предлагают различные правила дележа, приведем наиболее распространенные из них. Самое простое правило дележа- это правило «уступать иделить» (CD), которое справедливо для случая N =
. Вектор требований агентов выглядит (
), величина общих выплат равна M. Тогда первый агент претендует на сумму 
, уступая тем самым M
, если эта разность положительна и 0 в противном случае. Аналогично поступает и второй агент. Итак, получаем
=
и 
=
.
Далее выплачиваем каждому агенту цену уступки другого, а оставшуюся сумму денег делим пополам.
(d, M) =
+ 
(M 
), где i, jN и i ≠ j.
Рассмотрим еще одно правило дележа, которое является одним из самых распространенных в реальных задачах. Существует два типа пропорционального правила.
а) Правило усеченных претензий (TP). Здесь делёж вычисляется пропорционально усеченным претензиям min (, M).
TP(d, M) = αd
, где d= (
), 
= min(, M), α =
.
б) Приведенное правило (A). Это правило- одно из обобщений правила «уступать и делить». Сначала каждому агенту отдается сумма уступки от остальных, т. е. остаток при условии, что все кроме рассматриваемого агента удовлетворили свои требования.
(d, M) =
, m(d, M) = ((d, M
.
А вектор остатков dm(d, M) делится по правилу (а), c учетом, что осталась сумма 
= M
(d, M).
A(d, M) = m(d, M) + TP(dm(d, M),
).
Следующие правила основаны на идее уравнивания. Но главный вопрос состоит в том, по какому именно критерию уравнивать, если агенты не одинаковы. В задаче о банкротстве участники отличаются лишь величиной требований и уравнивание выплат игнорирует эти отличия. Получается, что агент может получить сумму большую чем ту, на которую претендует, но это противоречит нашему определению дележа. Поэтому в правиле ограниченных равных (CEA)выплат вводятся верхние границы выплат, и никто не получит больше, чем требует.
CE
(d, M) = min
, где 
удовлетворяет 
= M.
Существует иной подход к идее равенства- ограниченное эгалитарное правило (CE), которое основано на проблеме справедливого дележа в ситуации одновершинных предпочтений. Это правило концентрирует внимание на половине требований агентов, но модернизирует идею равномерного правила, что гарантирует одинаковую упорядоченность выплат и требований.
C
(d, M) = min, если выполняется 
≥ M
C(d, M) = max{
, min}, в противном случае.
В каждом случае выбирается так, что 
= M.
Еще одно правило дележа, использующее идею равенства — правило Талмуда (Т). Это правило можно объяснить с помощью простого алгоритма. Положим, что распределяемая сумма колеблется в пределе от 0 до половины суммарного требования. На первом шаге она будет делиться среди всех агентов равномерно до тех пор, пока каждому не достанется величина, которая равна половине минимальной претензии. Затем доля агента с минимальным требованием прекращает расти, а остаток делится между всеми поровну до того момента, пока все не получат сумму второй по минимальности заявки. Этот процесс будет продолжаться, пока распределяемая сумма не будет равна D/2. В этот момент каждый получит ровно половину своей заявки.
В случае, когда доступная сумма больше половины суммарного требования, будем уменьшать её и делить разность D — M. Сначала эта разность делится до того момента, пока каждый агент не получит убыток, равный половине наименьшей заявки. Аналогично процесс будет идти до тех пор, пока доступная сумма не будет равна D/2.
Если 
> M, тогда 
(d, M) = min{,
}, λ: 
= M.
Если < M, тогда (d, M) = — min{,}, λ:
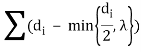= M.
Каталог теоретических правил дележа постоянно анализируется и пополняется, рассматриваются различные подходы к сравнению всех этих правил, вводятся семейства правил, которые содержат бесконечное число членов.
С другой стороны, цель распределения- удовлетворить потребности кредиторов, истцов и заявителей. А они в свою очередь хотят максимизировать свою часть выплат. Поэтому для решения этой проблемы логично использовать математическое моделирование средствами теории кооперативных игр. Такие игры моделируют ситуации, при которых участники игры, объединяясь, могут получить дополнительную прибыль.
Чтобы построить игровую модель банкротства предприятия, необходимо упомянуть некоторые сведения из теории кооперативных игр. Под игрой мы будем понимать процесс, в котором участвуют две и более сторон, ведущие борьбу за реализацию своих интересов. Пусть условия игры допускают совместные действия и перераспределения выигрыша. Главная задача исследования — это оптимальное распределение благ между членами объединения.
Построим игру в виде характеристической функции. Пусть N = {1,...,n} — множество всех игроков. Любое непустое подмножество S
будем называть коалицией.
Под характеристической функцией игры n лиц будем понимать вещественную функцию v, определенную на коалициях S
N, при этом для любых непересекающихся коалиций 
и S
N выполняется неравенство
(T) + (S) 
(T
S).
Это неравенство называется свойством супераддитивности. Оно необходимо для содержательной интерпретации числа (T) как гарантированного выигрыша коалиции Т в случае, когда она действует независимо от других игроков. Это означает, что объединение T
имеет не меньше возможностей, чем две непересекающиеся коалиции T и S, действующие в одиночку.
Построим характеристическую функцию на основе ранее рассмотренных правил дележа:
(S) = max{M — 
, 0}, S N, i N \ S. (*)
Таким образом поставим каждой коалиции в соответствие число равное сумме уступок игроков, которые не входят в эту коалицию.
При решении игры банкротства можно использовать различные принципы оптимальности такие как C-ядро, NM-решение, вектор Шепли. Но в данной задаче важно существование и единственность дележа для любой кооперативной игры. Поэтому удобно использовать принцип оптимальности- вектор Шепли, который вычисляется по следующей формуле:
= 
(
.
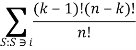Таким образом, в зависимости от исходных данных задачи мы можем выбрать подходящий принцип оптимальности. Поэтому кооперативная модель проблемы банкротства имеет преимущество перед теоретическими правилами распределения. Для того, чтобы определить справедливое решение, достаточно построить игру, проанализировать возможные решения и выбрать одно из них.
Иногда возникают ситуации, когда при ликвидации фирмы денежные средства поступают на счет руководства по временным периодам. Это может быть связано с банковскими особенностями, наличием у фирмы обособленных подразделений и другими экономическими факторами. Тогда распределение денежных средств производится по шагам и сложность дележа возрастает в несколько раз. Предложим подход для решения этой задачи, который строится на основе многошаговой кооперативной теории.
Предположим, что нам известна процедура поступления денежных средств на счет должника. Выплаты будут производиться в моменты времени (
,..., 
). Тогда вектор доступной суммы будет иметь вид (М
Стоит вопрос, каким образом осуществлять дележ в каждый момент поступления. На первом шаге построим одношаговую игру в виде характеристической функции (*) 
= (N,
), положим что M = M() +... + M(), вектор требований имеет вид (
, …,
). Строим характеристическую функцию и определяем вектор Шепли 
= (
,..., 
). На втором шаге уменьшим доступную сумму M = M(
) +... + M() и проделаем такие же вычисления. Аналогично процесс будет идти до шага m. После этого введем выплаты в каждый момент поступления:
= (
,..., 
) = 
-
.
...
= (
,..., 
) = 
.
…
= (
,..., 
) = 
.
Итак, мы получили новый подход к решению задачи возврата долгов кредиторам предприятия, основанный на поэтапном погашении задолженности. Серьезным шагом в математическом моделировании данной задачи будет построение игровых многошаговых моделей при помощи других принципов оптимальности. Это поможет избежать ряд юридических споров, и облегчит процедуру банкротства.
Литература:
- Aumann R., Maschler M. Game theoretic analysis of a bankruptcy problem from the Talmud. Journal of Economic Theory, 1985. Vol. 36, No 1. P.195–213
- Guiasu S. Three ancient problems solved by using the game theory logic based on the Shapley value. Knowledge, Rationality and Action, 2011. Vol.181, No 1. P. 65–79
- Петросян Л. А., Зенкевич Н. А., Шевкопляс Е. В. Теория игр. М.:БХВ-Петербург, 2014. 423 с.
