Введены понятия замечательный квадрат и средняя арифметическая площадь треугольника. С помощью их исследованы такие проблемы математики, как проблема бесконечно малых и бесконечно больших величин, проблема параллельных прямых, проблема континуума Кантора.
- Замечательный квадрат. Рассмотрим единичный квадрат K≡ A1ABB1, сторона которого является единичным отрезком; |AA1| = 1 (рис. 1). Проводим прямую CC, содержащую в себе отрезок A1B1. Определим на луче A1C пункты C2, C3, …,Cn, … так, чтобы |A1B1| = |B1C2| = |C2C3| = … = |Cn–1Cn| = …. Проводим наклонные отрезки AB1,AС2, AC3, …,ACn, …, пересекающие отрезок B1B в пунктах B2, B3, …,Bn, … соответственно. Из этих пунктов проводим горизонтальные отрезки A2B2, A3B3,…, AnBn, …, соединяющие две стороны A1A и B1B и параллельные в смысле Евклида стороне A1B1 квадрата K. Единичный квадрат K вместе с горизонтальными A2B2, A3B3,…, AnBn, … и наклонными отрезками AB1,AB2, …,ABn, … называется замечательным квадратом.
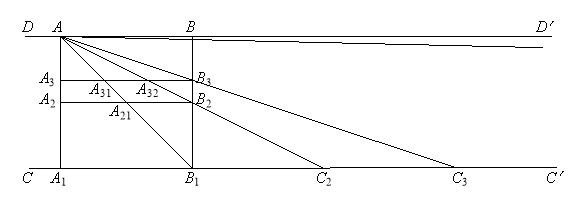
Рис. 1.
Теорема 1. В замечательном квадратеK=A1ABB1: 1) горизонтальные отрезкиA2B2, A3B3,…, AnBn, … расположены так, что |B1Bn| = 1–1/n; 2)наклонные отрезкиAB1,AB2, …,ABn–1разделяют горизонтальный отрезокAnBnнаn равных частей длины1/n.
Доказательство. Наклонные отрезки AB1,AB2, …,ABn–1 пересекают горизонтальный отрезок AnBn в точках An1, An2, …, An,n–1 и разделяют его на n частей. Из подобия треугольников AAnBn и AA1Cnследует: |AAn| = 1/n, |B1Bn| = 1– 1/n. Из пропорций
![]()
следует утверждение теоремы.
-
Средняя арифметическая площадь треугольника. Обозначим через L() пря-мую, проходящую через точку P под углом =
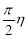 (0 1) к перпендикуляру PQ, опущенному на прямую AA (рис. 2). Заметим, что L(1) представляет собой параллельную к AA прямую BB, а L(0) — перпендикулярную к AA прямую PQ. Откладываем на луче QAотрезки QQ1, Q1Q2, …, Qn–1Qn, …, равные PQ. В пунктах Q1, Q2, …, Qn, … луча QA восстановим перпендикуляры Q1P1, Q2P2, …, QnPn, …. В результате полоса BPQA разбивается на квадраты. Прямая L() пересечет Q1P1 в пункте L1, Q2P2 в пункте L2 и т. д. (рис. 2).
(0 1) к перпендикуляру PQ, опущенному на прямую AA (рис. 2). Заметим, что L(1) представляет собой параллельную к AA прямую BB, а L(0) — перпендикулярную к AA прямую PQ. Откладываем на луче QAотрезки QQ1, Q1Q2, …, Qn–1Qn, …, равные PQ. В пунктах Q1, Q2, …, Qn, … луча QA восстановим перпендикуляры Q1P1, Q2P2, …, QnPn, …. В результате полоса BPQA разбивается на квадраты. Прямая L() пересечет Q1P1 в пункте L1, Q2P2 в пункте L2 и т. д. (рис. 2).
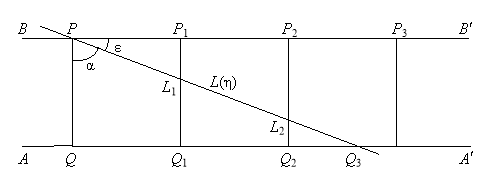
Рис. 2.
Примем длину отрезка PQ равной единице. Пусть s1 — площадь трапеции PL1Q1Q, s2 — площадь трапеции L1L2Q2Q1 и т. д. Если прямая L() не пересечет QnPn, то положим sn+1 = sn+2 = … = 0. Площадь треугольника T(), ограниченная прямыми PQ, QA, L() определяется суммой
Рассмотрим числовую последовательность {n, n≥1}, удовлетворяющую условие tg![]() n = n. Отсюда имеем n=
n = n. Отсюда имеем n=![]() arctgn, nN.
arctgn, nN.
1. Пусть прямая L(n) пересекает луч QAв точке Qn. Тогда n = nи площадь треугольника PQQn равна Sn [L(n)] = n/2. Отсюда имеем g [L(1– o)] = ½.
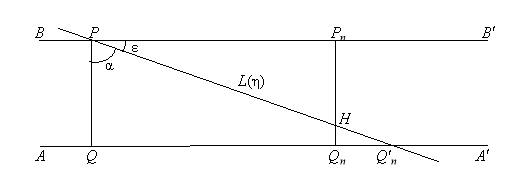
Рис. 3.
2. Пусть прямая L(n) пересекает луч QAв точке Qn (рис. 3), лежащей за точкой Qn. Тогда n>n. Положим: |QQn| = cn, c > 1 (c= const). Прямая L(n) пересекает перпендикуляр PnQn в точке H. Отрезок QnH имеет длину x. Треугольники PQQn и HQnQn подобны, поэтому имеют место равенства 1/cn= x/(cn — n), x= 1–1/c. Отсюда находим площадь трапеции QQnHPSn [L(n)] = (1–1/2c)n. Следовательно, g [L(1– o)] = 1–1/2c.
3. Пусть в пункте 2 точка Qn лежит перед точкой Qn. Тогда n < n. Положим |QQn| = n/c, c>1. Площадь треугольника PQOnSn [L(n)] = n/2c. Отсюда имеем g [L(1– o)] = 1/2c. Заметим, что если в пп. 2 и 3 положить c= 1, то получится результат п. 1.
4. Пусть в п. 2 |QQn| = 2n. Тогда справедливы соотношения:
Sn [L(n)] = ![]() g [L(1– 0)] = 1.
g [L(1– 0)] = 1.
5. Пусть в п. 3 |QQn| =![]() . Тогда справедливы соотношения:
. Тогда справедливы соотношения:
Sn [L(n)] =
Длину отрезка QQn можно выразить через угол QPQn = ![]() (рис. 3) в виде равенства |QQn| = tg
(рис. 3) в виде равенства |QQn| = tg![]() , которое может быть использовано для нахождения средней арифметической площади различных треугольников T().
, которое может быть использовано для нахождения средней арифметической площади различных треугольников T().
6. Пусть n = 1 — /n, где — положительное число. Предположим, что n < n. Тогда
g [L(1– o)] = ![]() =
=![]() tg
tg![]() .
.
Поскольку точка Qn лежит перед точкой Qn, то 1/ < 1/2 или > 2/.
7. Пусть в п. 6n>n. Длина отрезка PnH равна y= n tg![]() (рис. 3). Так как x= 1 — y(см. п. 2), площадь трапеции QQnHPравна Sn [L(n)] = (1 — y/2)n. Отсюда имеем
(рис. 3). Так как x= 1 — y(см. п. 2), площадь трапеции QQnHPравна Sn [L(n)] = (1 — y/2)n. Отсюда имеем
g [L(1– o)] = ![]() =
=![]()
Поскольку Qn лежит за точкой Qn, то 1/2 < 1– /4 < 1 или 0 < < 2/.
Заметим, что если в пп. 6 и 7 положить = 2/, то получится g [L(1 — o)] = ½. Такой же результат получится, если в п. 1 точки Qn и Qn совпадают.
8. Пусть n= 1–1/![]() . Тогда n < n и также как в п. 6 получим
. Тогда n < n и также как в п. 6 получим
g [L(1– 0)] = 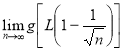 =
=![]() tg
tg![]()
9. Пусть n= 1–1/2n. Тогда n > n и также как в п. 7 получим
g [L(1– 0)] = ![]()
![]()
- Предел бесконечного деления. Полученные результаты могут быть рассмотрены как геометрическая интерпретация следующих пределов
![]()
Далее, с помощью замечательного квадрата будем изучать числовую последовательность {1/n, n≥1}, пределом которой является число нуль ничто. В силу этого, соответствующая последовательность отрезков {AnBn, n≥1} стремится к отрезку АВ (рис. 1), которая представляет собой континуум (не имеет частей ни один из отрезков ABn, nN = {1, 2, …, n, …} не пересечет АВ), ибо каждая часть деления AnАnm в процессе деления укорачивается, стремится исчезнуть.
Отрезок AnBn с точками разделения AnАn1, AnАn2, AnАn3, … AnАnn-1 замечательного квадрата представим на отдельном рисунке 4.
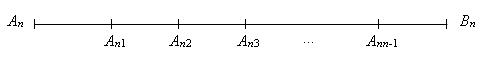
Рис. 4.
Если взят ВВn = AnАn1 в качестве эталона длины (единичного отрезка), то AnВn имеет длину n, что можно выразить в виде отношения
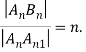 (1)
(1)
Поскольку |AnBn| =1, |AnAn1| =1/n, то равенство (1) может быть представлено в виде
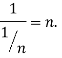 (2)
(2)
Когда 1/nстремится к нулю, n, как длина отрезка при эталоне длины AnАn1, стремится к мощности континуума, ибо AnBn стремится к АВ. По Кантору континуум как множество точек отрезка имеет мощность континуума с. Следовательно, имеет место утверждение: когда 1/n 0, то nc, а не к бесконечности, выражаемой символом . Здесь бесконечность понимается как бесконечное множество единиц: = {1, 1, 1, …}. Мощность (число элементов) бесконечного множества единиц обозначают буквой омега , хотя и , и имеют одно и то же смысл.
Исходя из сказанных и равенства (2) мощность континуума символически может быть представлена в виде равенства
![]() (3)
(3)
- Проблема бесконечно малых ибесконечно больших величин. Континуум как отрезок реален, а по поводу реальности бесконечного множества нет однозначного ответа, имеется всего лишь аксиома бесконечности: бесконечное множество существует (Бурбаки) [1, c. 21].
Следующая цепочка рассуждений приводит к выводу, затрагивающему основание математики:
Вселенная бесконечна существует луч CC' (рис. 1) множество натуральных чисел N существует актуально множество отрезков {AB1, AC2, AC3, …, ACn, …} (рис. 1) существует актуально в замечательном квадрате имеется отрезок AB, состоящий из бесконечного числа равных частей AA1, A1A2, A2A3,..., A,m-1Am,..., длина которых равна ![]() .
.
Каждая из частей A,m-1Am (m ≥1) имеет протяженность, но она по сравнению с отрезком AB, в котором таких частей бесконечное множество, равна нулю ![]() , ибо 1 = (луч, имеющий бесконечную длину, не станет длиннее, если к началу его прибавляется единичный отрезок, не станет короче, если от начала отнимается единичный отрезок). Между тем, A,m-1Am не точка, а отрезок, поэтому ее длина не истинный (абсолютный), а вырожденный (относительный) нуль. Вырожденного нуля обозначим буквой о. Отсюда имеет место равенство
, ибо 1 = (луч, имеющий бесконечную длину, не станет длиннее, если к началу его прибавляется единичный отрезок, не станет короче, если от начала отнимается единичный отрезок). Между тем, A,m-1Am не точка, а отрезок, поэтому ее длина не истинный (абсолютный), а вырожденный (относительный) нуль. Вырожденного нуля обозначим буквой о. Отсюда имеет место равенство ![]() . Следовательно,
. Следовательно, ![]() . Ввиду (3) данное отношение может быть названо вырожденным континуумом.
. Ввиду (3) данное отношение может быть названо вырожденным континуумом.
Здесь уместно взглянуть в историю бесконечно малых величин.
Когда в первой половине XVII в. Кеплер и Кавальери ввели в научное употребление понятие бесконечно малой величины, то она представлялась им как актуальная бесконечно малая величина, постоянная и неизменная, образующаяся в итоге завершения процесса бесконечного деления конечной величины. На эту точку зрения встали и другие математики того времени [2, c. 94].Много сделал для того, чтобы утвердить концепцию бесконечной делимости, Л. Эйлер. Он опирался при этом, по-видимому, не столько на математику, сколько на физику и даже биологию, отмечая, что протяженность всегда имеет величину, а всякая величина делима. Чем больше частей, тем они ближе будут к нулю, «но сущими нулями не будут», пишет он «…Два нуля могут иметь друг другу любое геометрическое отношение», пишет Эйлер, и поэтому нельзя смешивать различные нули, которыми являются различные бесконечно малые величины. Все же диалектическая идея Эйлера о содержательности нуля не нашла последователей среди крупных математиков не столько из-за несообразностей в рассуждениях, сколько из-за всеобщего распространения метафизического мышления [3, c. 71].
Поскольку вырожденный нуль равен абсолютному нулю, то вырожденный континуум равен континууму, т. е.
= с.
Это равенство может быть истолковано как, как «бесконечность есть континуум». Именно такую трактовку в свое время выдвигал Лейбниц.
Г. В. Лейбниц, размышляя о непрерывности отметил: «Все непрерывное бесконечно» [3, с. 51]. Он в соответствии с принципом непрерывности своей философии понимает «истинное бесконечное» как не имеющее частей, нерасчлененное абсолютное. «Истинная бесконечность, — пишет он, — в точном смысле слова заключается лишь в абсолютном, которое предшествует всякому соединению и не образовано путем прибавления частей» [3, с. 44–45].
Итак, бесконечно малые величины — это вырожденные нули, а бесконечно большие величины это вырожденные континуумы. Бесконечность есть континуум.
-
Проблема параллельных прямых. Как было выяснено в п. 4, из посылки «множество натуральных чисел N существует актуально» следует вывод «в замечательном квадрате имеется отрезок AB, состоящий из бесконечного числа равных частей, длина которых равна
 ». Если через точек A и B провести прямую, то она имеет такое положение L(η*) в полосе DD'C'C (рис. 1), что средняя арифметический площадь треугольника Т(η*) равна ½. Действительно, числовая последовательность {1/n, n≥1} стремясь к нулю достигнет вырожденного нуля 1/ = о. Соответствующая числовая последовательность прямых {L(ηn), n≥1}, где
». Если через точек A и B провести прямую, то она имеет такое положение L(η*) в полосе DD'C'C (рис. 1), что средняя арифметический площадь треугольника Т(η*) равна ½. Действительно, числовая последовательность {1/n, n≥1} стремясь к нулю достигнет вырожденного нуля 1/ = о. Соответствующая числовая последовательность прямых {L(ηn), n≥1}, где 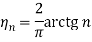 (см. п. 1°) достигнет такого положения L(η) при котором g [L(η)] = ½. Если рассмотреть числовую последовательность {n, n≥1}, где
(см. п. 1°) достигнет такого положения L(η) при котором g [L(η)] = ½. Если рассмотреть числовую последовательность {n, n≥1}, где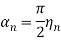 (см. п. 2), то когда 1/n 0 величина ηn η = 1 о', а угол n =
(см. п. 2), то когда 1/n 0 величина ηn η = 1 о', а угол n = 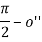 (вырожденному прямому углу), где o'' =
(вырожденному прямому углу), где o'' = 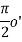 вырожденный нуль.
вырожденный нуль.
Прямая L(η), частью которой является луч AC', представляет собой параллельную в смысле Лобачевского прямой CC' по направлению A1C' для точки А. Следует заметить, что отрезок АВ является частью луча AC'. В геометрии Лобачевского прямая DD' (рис. 1) называется сверхпараллельной линией к прямой СС'. Эти рассуждения позволяют сформулировать теорему.
Теорема 2. Аксиома Лобачевского о параллельных прямых верна.
Идея Эйлера о различных нулях свое время была игнорирована, и это привело к тому, что угол ε между прямыми L(η) и DD' т. е.угол ВАВбыл принять Лобачевским больше нуля, а в самом деле он представлет собой вырожденный нуль ε = ![]() .
.
- Проблема континуума Кантора. Заметим, что tg(A1AC') = tg(A1AВ) = (луч A1C' имеет длину ) и tg(A1AD') = tg(A1AВ) = с (отрезок АВ не имеет частей).
Континуум-гипотеза Кантора может быть сформулирована так: между лучамиACи ADникаких лучей, исходящих из точкиA не существуют. Возможно и такая трактовка континуум-гипотезы: между отрезкамиABи A Вникаких отрезков не существуют. Но отрезок BВ в замечательном квадрате может быть разделен на две части. Это значит, что между отрезками ABи AВможет находиться еще один отрезок AВ. Из этих рассуждений вытекает следующая
Теорема 3. Между мощностью и мощностью континуума с имеется промежуточ-ная мощность .
Следствие 1. Континуум- гипотеза Кантора неверна.
- Множество натуральных чисел. Для полноты изложенных результатов, представим теорему, касающейся множества натуральных чисел.
В основе математики лежит следующее
Высказывание 1. Каждый элемент множества натуральных чисел N конечное число, а само N — бесконечное множество.
Насколько верно такое утверждение покажет следующая
Теорема 4. Если бесконечное множество единиц = {1, 1, 1, …} существует, то оно является элементом множества натуральных чисел, т. е. N.
Доказтельство. Рассмотрим бесконечную прямоугольную матрицу
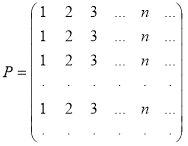 .
.
Каждая строка Pn, диагональ D, совокупность номеров строк S матрицы P представляет собой множество натуральных чисел N. Удалим из P все наддиагональные элементы. В результате получим бесконечную треугольную матрицу
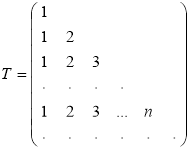 .
.
Tn —n-я строка матрицы T представляет собой отрезок Nn = {1, 2, 3, …, n} множества натуральных чисел N. В этой связи матрица T может быть представлена в виде T = {N1, N2,N3, …}. Согласно высказыванию 1 каждый отрезок Nn из T имеет конечную длину или, то же самое, каждая строка Tn матрицы T содержит конечное число элементов. Это значит, что у матрицы T нет строки с бесконечным числом элементов, т. е. NT.
Между тем, когда удаляются наддиагональные элементы матрицы P, число столбцов «не уменьшается», оно остается быть бесконечным. Этот факт может быть установлен из следующих соображений. Обозначим n-й столбец матрицы P, состоящий из одних n, через En. Матрицу P представим в виде P= {E1,E2,E3, …}. В диагонали D каждый столбец En имеет своего «представителя» — число n. Когда удаляются наддиагональные элементы матрицы P, часть элементов столбцов E1,E2,E3, … исчезает, но ни один из них не исчезает полностью, ибо элементы диагонали D остаются в сохранности. Отсюда можем заключить, что матрица T имеет бесконечное число столбцов. А это возможно только в том случае, когда матрица T имеет строку с бесконечным числом элементов, т. е., когда NT.
Таким образом, если мы исходим из положения, что каждый элемент множества натуральных чисел N является конечным числом, то приходим к выводу NT. Если же мы исходим из положения, что множество натуральных чиселNявляется бесконечным множеством, то приходим к выводу NT. Отсюда следует
Следствие 2. Высказывание 1 ложно.
Понятия «замечательный квадрат» и средняя арифметическая площадь треугольника» появились в результате исследования марковской игры «Большой матч» [4–7].
Литература:
- Наан Г. И. Понятие бесконечности в математике и космологии // Бесконечность и Вселенная. М.: Мысль, 1969. 325 с.
- Свидерский В. И., Кармин А. С. Конечное и бесконечное: Философский аспект проблемы. М.: Наука, 1966. 320 с.
- Бурова И. Н. Развитие проблемы бесконечности в истории науки. На материалах истории философии и математики. М.: Наука, 1987. 134 с.
- Ибрагимов А. А. Существование значения в общих марковских играх // Известия РАН. Теория и системы управления. 2004. № 2. С.5–15.
- Ибрагимов А. А. Марковская игра «Большой матч» в классе стационарных стратегий // Журнал «Молодой ученый» № 4 (84), март, 2015 г. Москва. С. 4–7.
- Ибрагимов А. А. Решение общей марковской игры путем аппроксимации ее игрой с переоценкой // Журнал «Молодой ученый» № 13 (117), июль-1, 2016 г. Москва.







