Данная работа посвящена модели патентных гонок пуассоновского типа. Рассмотрен частный случай патентной гонки между монополистом и новичком на рынке, найдена ситуация равновесия по Нэшу.
В данной статье рассмотрена модель патентной гонки пуассоновского типа между монополистом (игрок 1, А) и новичком (игрок 2, Е). В ней мы учитываем затраты на текущие исследования и разработки(ИР) и не берем в рассмотрение опыт, накопленный двумя игроками раннее, что существенно упрощает нам анализ данной модели. Патентная гонка пуассоновского типа дает ответ на вопрос, является ли монополист более склонным к инновациям, чем новичок. Сам патент, за который борются игроки, может послужить как улучшению технологии производства определенного продукта, так и созданию нового товара в сегменте рынка, который до инновации занимала первая фирма — монополист. Предполагается, что фирма, которая первой осваивает новую технологию, приобретает и использует патент, который имеет неограниченный срок действия. Конкуренция в области ИР между двумя фирмами характеризуется интенсивностями инвестиций на исследования, заданными в виде функций времени ![]() ∈
∈![]() и
и ![]() ∈
∈![]() , t∈
, t∈![]() . В каждый момент t, если ни одна из фирм не сделала открытие, игра, начавшаяся в этот момент, идентична первоначальной. Поэтому стратегии игроков
. В каждый момент t, если ни одна из фирм не сделала открытие, игра, начавшаяся в этот момент, идентична первоначальной. Поэтому стратегии игроков ![]() и
и ![]() не зависят от времени. Так как мы рассматриваем патентную гонку без памяти, то время, когда фирма i сделает открытие будет иметь экспоненциальное распределение и вероятность для фирмы сделать открытие в момент t будет зависеть только от интенсивности ее инвестиций в этот период. Будем предполагать, что функция распределения
не зависят от времени. Так как мы рассматриваем патентную гонку без памяти, то время, когда фирма i сделает открытие будет иметь экспоненциальное распределение и вероятность для фирмы сделать открытие в момент t будет зависеть только от интенсивности ее инвестиций в этот период. Будем предполагать, что функция распределения ![]() того, что фирма i сделает открытие до момента t при уровне инвестиций xимеет вид:
того, что фирма i сделает открытие до момента t при уровне инвестиций xимеет вид:
![]()
Где ![]() - время, когда фирма iсделает открытие, h(x) – заданная дважды дифференцируемая функция, удовлетворяющая следующим условиям:
- время, когда фирма iсделает открытие, h(x) – заданная дважды дифференцируемая функция, удовлетворяющая следующим условиям:
![]()
![]()
![]()
![]()
В предположениях модели:
![]()
Данное выражение следует из свойств экспоненциального распределения, позволяющего не учитывать опыт и знания, которые фирмы накопили ко времени t, т.е.
Пусть игра начинается в момент ![]() и заканчивается, когда одна из фирм сделала первой открытие, т.е. выиграла патентную гонку. Пусть
и заканчивается, когда одна из фирм сделала первой открытие, т.е. выиграла патентную гонку. Пусть ![]() – время, когда фирма iпервой сделает открытие в патентной гонке, т.е.
– время, когда фирма iпервой сделает открытие в патентной гонке, т.е. ![]() Тогда
Тогда ![]() также имеет экспоненциальное распределение F(t). По определению функции распределения:
также имеет экспоненциальное распределение F(t). По определению функции распределения:
![]()
По свойству распределения вероятностей
![]()
По условию, что ![]() , получаем
, получаем
![]()
![]()
Так как ![]() – независимые величины. Используем снова определение функции распределения
– независимые величины. Используем снова определение функции распределения
![]()
Тогда
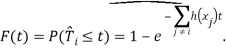
Пусть ![]() прибыль монополиста до получения патента,
прибыль монополиста до получения патента, ![]() его прибыль, если он выиграл патентную гонку и
его прибыль, если он выиграл патентную гонку и ![]() если проиграл,
если проиграл, ![]() прибыль новичка, если он первый сделал открытие. Тогда интегральный выигрыш в игре с предписанной продолжительностью
прибыль новичка, если он первый сделал открытие. Тогда интегральный выигрыш в игре с предписанной продолжительностью ![]() , выражается следующим образом:
, выражается следующим образом:
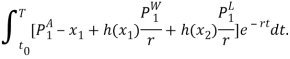
Где ![]() – заданная процентная ставка.
– заданная процентная ставка.
Так как в нашей постановке момент окончания игры ![]() – величина случайная, то под выигрышем в игре будем понимать математическое ожидание от интегрального выигрыша, т.е.:
– величина случайная, то под выигрышем в игре будем понимать математическое ожидание от интегрального выигрыша, т.е.:
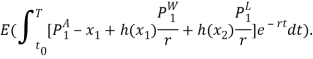
Таким образом, ожидаемый выигрыш представляет собой следующий интегральный функционал:
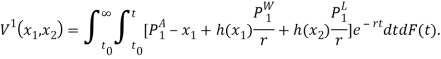
С помощью перестановки интегралов в интегральном функционале, ожидаемый выигрыш может быть представлен в виде:
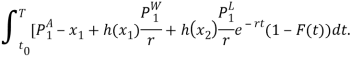
Т.е.:
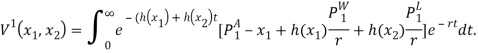
Рассуждая аналогично, ожидаемая прибыль новичка вычисляется следующим образом.
Интегральный выигрыш новичка:
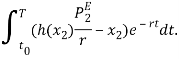
Ожидаемый выигрыш новичка:
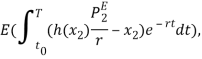
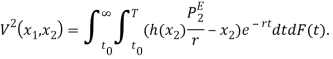
Переходим от двойного интеграла к следующему виду:
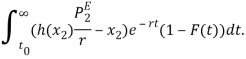
Т.е.:
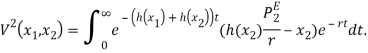
Вычисляя интегралы, мы получаем выигрыши игроков в явном виде:
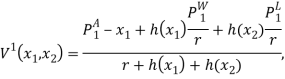
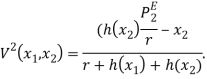
В итоге мы построим бесконечную игру двух лиц в нормальной форме: ![]() где
где ![]() -множества стратегий игрока 1 и 2, а функции выигрыша
-множества стратегий игрока 1 и 2, а функции выигрыша ![]() заданы в явном виде по формулам, представленным выше.
заданы в явном виде по формулам, представленным выше.
Рассмотрим вторые частные производные от ![]() :
:
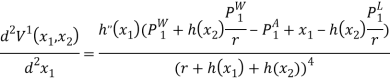
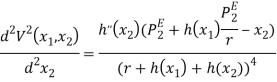
Учитывая полученный результаты и предположения относительно свойств ![]() , в игре
, в игре ![]() существует равновесие по Нэшу в чистых стратегиях, которое находится из условий первого порядка:
существует равновесие по Нэшу в чистых стратегиях, которое находится из условий первого порядка:
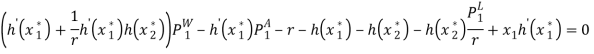
![]()
В общем случае, система, составленная из двух представленных уравнений не имеет аналитического решения.
Литература:
- Tirole J. The Theory of Industrial Organization. London: The MIT Press, 1990. P. 619–623.







