Вейвлет-анализ в настоящее время является удобным инструментом, способным решать многие практические задачи. Вейвлет-анализ применяется в различных областях науки и техники. Широкое применение приобретает решения электроэнергетических вопросов, а именно в таких направлениях как анализ качества электроэнергии, релейная защита электроэнергетических систем, расчёты переходных процессов, диагностика электрического оборудования.
Преобразование Фурье для анализа стационарных синусоидальных и нестационарных несинусоидальных сигналов.
Преобразование Фурье переводит в частотный спектр амплитудно-временное представление сигнала. По полученному спектру можно говорить о наличии выделенных частот в сигнале
Имея во временном представлении зависимость амплитуды сигнала от времени и проведя преобразование Фурье можно получить сведенья об амплитуде сигнала с данной частотой [1].
Создаём в программе MATLAB стационарный сигнал тока.
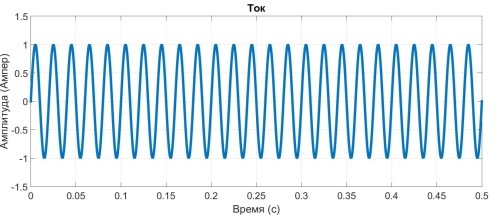
Рис. 1. Стационарный синусоидальный сигнал тока после дискретного преобразования Фурье
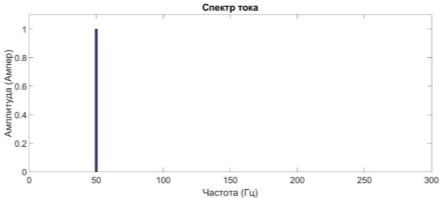
Рис. 2. Спектральный состав стационарного синусоидального сигнала тока
Таким образом проведя преобразование Фурье, мы получили амплитудно- частотное представление сигнала (рисунок 1, рисунок 2). По полученному спектру можно сказать, что в сигнале присутствует частота f=50 Гц. Однако в реальных сигналах присутствует большое количество различных частот.
Нестационарным называется сигнал тока, в котором присутствуют различные частоты на разных временных интервалах. Смоделируем нестационарный сигнал тока (рисунок 3, рисунок 4).
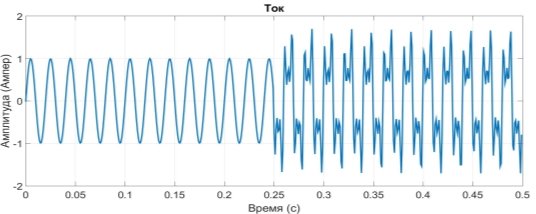
Рис. 3. Нестационарный сигнал тока с присутствием разных частот после дискретного преобразования Фурье
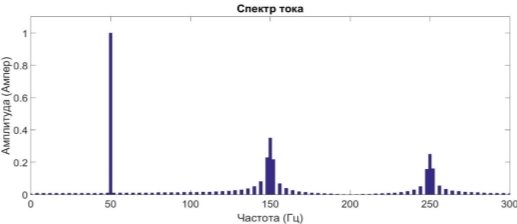
Рис. 4. Спектральный состав нестационарного сигнала тока
Из полученных графиков видно, что имеются два временных промежутка, первый от 0 до 0,25 с, второй от 0,25с. до 0,5с. На первом временном интервале присутствует частота f=50 Гц, на втором временном интервале присутствуют частоты f=50 Гц, f=150 Гц и f=250 Гц.
Мы видим, что в случае нестационарного сигнала существует растекание спектра, с которым преобразование Фурье не справляется
Применение вейвлет-преобразования для анализа сигналов.
В настоящее время большую популярность для анализа нестационарных режимов в электроэнергетике приобрело вейвлет-преобразование. Так как оно решает те недостатки, которые присуще преобразованию Фурье.
Любое вейвлет-преобразование основано на двух функциях: масштабирующая (апроксимирующая) и вейвлет-функция (детализирующая).
Аппроксимирующей называется функция со значение интеграла равным единице. С помощью этой функции осуществляется аппроксимацию сигнала, то есть грубое приближение. Такие функции необходимы при анализе низкочастотных и высокочастотных компонент в сигнале.
Детализирующей называется функция, имеющая значение интеграла равное. При анализе используются хорошо локализованные функции как во временной области, так и в частотной. С помощью этой функции выделяются локальные особенности сигнала и его детали.
Применим дискретное вейвлет-преобразование к стационарному сигналу тока. Покажем на рисунке 5 сигнал тока и полученные после дискретного вейвлет-преобразования апроксимирующие и детализирующие коэффициенты, полученные с помощью вейвлета Хаара и вейвлета Добеши 4 порядка. Разложение будем производить до уровня равным единице.
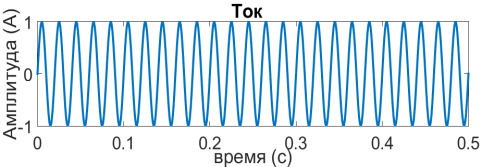
а)
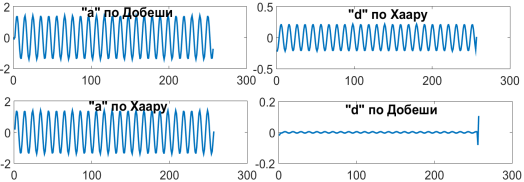
б)
Рис. 5. а- Стационарный синусоидальный сигнал тока; б- коэффициенты сигнала
И применим дискретное вейвлет-преобразование к нестационарного несинусоидальному сигналу тока. На рисунке 6 изобразим сигнал тока и полученные апроксимирующие и детализирующие коэффициенты после дискретного вейвлет-преобразования с помощью вейвлета Хаара и вейвлета Добеши 4 порядка.
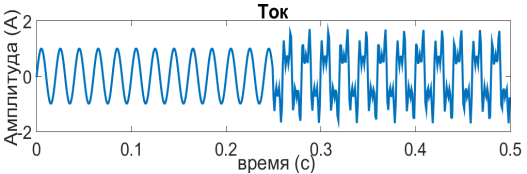
а)
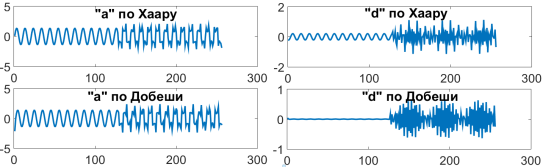
б)
Рис. 6. а) нестационарный несинусоидальный сигнал тока; б) коэффициенты сигнала
На данных графиках «a», «d» это апроксимирующие и детализирующие коэффициенты.
Вейвлет-преобразование позволяет получить временную и частотную информацию, сужая окно для выделения коротких высокочастотных участков или расширяя его для анализа длительных низкочастотных колебаний [2].
На рисунке 7 представим нестационарный сигнал после вейвлет-преобразования, которое наглядно показывает в трёхмерном пространстве картину изменения таких параметров как, амплитуда, частота и время.
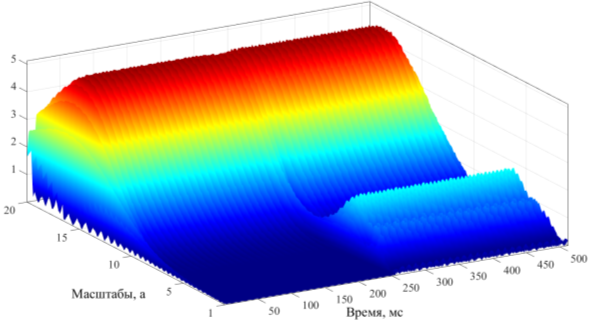
Вывод.
Вейвлет-преобразование решает недостатки присущие преобразованию Фурье, а именно растекание спектра сигнала. А также вейвлет-преобразование даёт частотно-временное представление сигнала, чтобы наглядно увидеть в какой момент времени сигнал был наполнен именно данной частотой.
Литература:
1. Нагорнов, О. В. Вейвлет-анализ в примерах [Текст]:учебное пособие / О. В. Нагорнов, В. Г. Никитаев, В. М. Простокишин, С. А. Тюфлин и др. — М.: НИЯУ МИФИ, 2010. — 120 с.
2. Захарова, Т. В. Вейвлет-анализ и его приложения: учеб. пособие / Т. В. Захарова, О. В. Шестаков. — М.: ИНФРА-М, 2012. — 150 с.







