В представленной работе исследуются различные методы повышения резкости цифровых изображений.
Ключевые слова: цифровые изображения, фильтр Собела, фильтр Лапласа
В современном мире визуальное восприятие является одним из основных источников получения информации человеком. Таким образом, многие отрасли, имеющие непосредственное отношение к получению, обработке, хранению и передаче информации ориентируются на то, чтобы она представлялась в виде изображений. Особое значения улучшение и коррекция изображения принимает при неразрушающем контроле и медицинской диагностике, а также научных исследованиях, проводимых различными рентгеновскими методами. По этой причине возникает инженерная задача по улучшению качества изображений для визуального восприятия и для оценки изображений техническими средствами. В настоящее время с этой задачей можно справиться только с использованием цифровых методов обработки.
1. Цифровое изображение в современном мире.
Цифровое изображение — это представление информации в виде функции двух переменных f(x, y), где x и y — пространственные координаты на плоскости, а сама функция определяет интенсивность или градацию серого в этой точке. Они состоят из конечного числа элементов, которые называются пикселями. Цифровое изображение удобно для хранения, передачи, преобразования по сравнению с аналоговыми изображениями и несет за собой большой информационный поток [1].
Для получения цифровых изображений используются фоточувствительные элементы. Самым простейшим устройством для регистрации уровня освещенности является фотодиод, сигнал на выходе которого, пропорционален уровню освещенности чувствительной области в данный момент. На аналогичном принципе строятся все приборы с зарядовой связью (ПЗС), так как каждый элемент ПЗС-матрицы представляет собой фоточувствительный элемент. Обычно для этого используются МДП конденсаторы, которые накапливают заряд и после с помощью управляющего потенциала заряд постепенно перетекает в соседние элементы ПЗС-матрицы.
2. Основы фильтров повышения резкости цифровых изображений.
Главная цель повышения резкости заключается в подчеркивании мелких деталей изображения или улучшении тех деталей, которые оказались расфокусированы вследствие неудовлетворительного качества съемки. Повышение резкости изображений используется в различных отраслях человеческой деятельности.
Повышение резкости достигается за счет пространственного дифференцирования. Дифференцирование усиливает перепады и другие разрывы и не выделяет области с медленными изменениями уровней яркости.
Производные дискретной функции определяются в терминах разностей. Первая производная должна быть: равной нулю на участках с неизменной яркостью; в остальных случаях она имеет ненулевое значение. Аналогично вторая производная должна быть: неравной нулю в начале и в конце ступеньки или склонах яркости; в остальных случаях принимает нулевое значение.
Производная первого порядка одномерной функции f(x) определяется как разность яркостей соседних пикселей:
![]() (1)
(1)
Аналогично, вторая производная определяется как разность соседних значений первой производной:
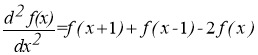 (2)
(2)
Для выделения сходства или различия между производными первого и второго порядков, рассмотрим пример на рисунке 1.
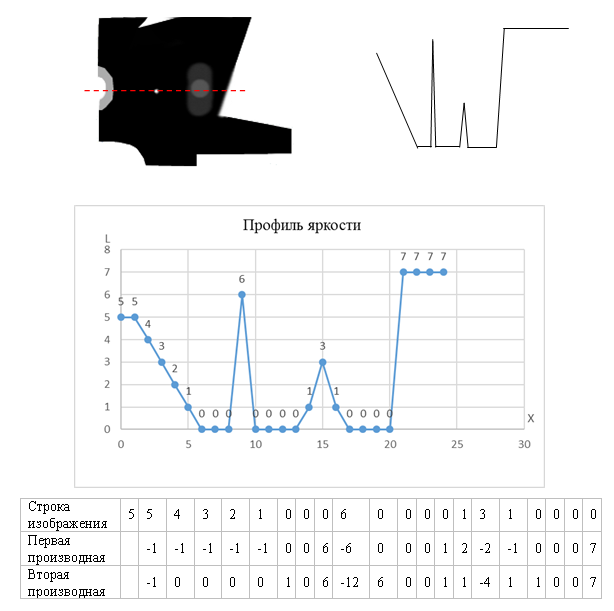
Рис. 1. Нахождение производных разных первого и второго порядков
На рисунке показана упрощенная дискретная схема профиля, содержащая минимальное количество точек, требуемое для анализа поведения первой и второй производных вблизи отдельной точки, линии, склона и контура объекта.
Рассмотрим поведение производных разных порядков при движении по горизонтальной оси изображения слева направо. Видно, что первая производная дает в результате «толстые» контуры, а вторая — значительно более тонкие. На отдельной точке отклик второй производной получается большим, поэтому она является более действенной для этой задачи.
Рассмотрим изотропные фильтры — эти фильтры инвариантные к повороту, т. е. при повороте изображения и последующее применение фильтра дает тот же результат, что и применение фильтра с последующим поворотом.
Простейшим изотропным оператором, который основан на производных, является лапласиан (оператор Лапласа), определяющийся как:
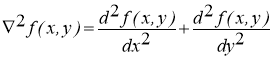 (3)
(3)
Для его записи в дискретном виде используют частные производные:
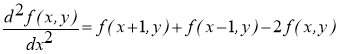 (4)
(4)
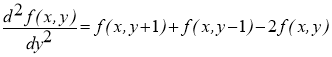 (5)
(5)
тогда лапласиан равен:
![]() (6)
(6)
Это уравнение может быть реализовано с помощью маски, которая представлена на рисунке 2 (a), дающая результат, который изотропен для поворотов на углы, кратные 90°.
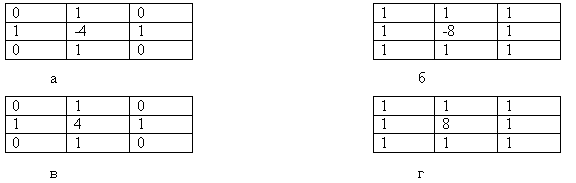
Рис. 2. Маски оператора Лапласа
Если используемая маска имела отрицательные центральные коэффициенты, тогда для повышения резкости, изображение-лапласиан следует вычитать, а не прибавлять.
В обработке изображений первые производные реализуются через модуль градиента, который определяется как вектор-столбец:
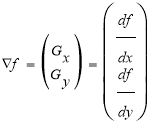 (7)
(7)
Модуль этого вектора равен:
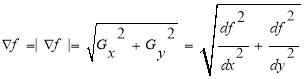 (8)
(8)
Компоненты вектора градиента являются линейными операторами, но модуль вектора, очевидно, нет, поскольку он выражается через операции возведения в квадрат и извлечения квадратного корня. С другой стороны, частные производные в уравнении (7) не являются инвариантными к повороту (изотропными), но модуль вектора градиента таковым является.
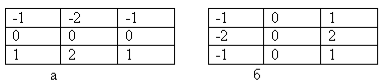
Рис. 3. Маски фильтров, основанных на первой производной
Уравнение 8 реализуется при помощи масок, представленных на рисунке 3 и называется оператором Собела. Маска 3(а) предназначена для нахождения горизонтальных контуров, а маска 3(б) для нахождения вертикальных контуров.
Заключение.
Представленные в работе методы дали возможность повышения резкости рентгеновских снимков объектов технических систем, что позволило повысить информативность данного типа изображений.
Литература:
- Гонсалес Р., Вудс Р. Цифровая обработка изображений. М.: Техносфера, 2005. 1071 с.
- Миронов Д. А. Большая энциклопедия цифровой фотографии. М.: Эксмо, 2012. 328 с.
- Фисенко В. Т., Фисенко Т. Ю., Компьютерная обработка и распознавание изображений: учеб. пособие. СПб: СПбГУ ИТМО, 2008. 192 с.
- JETCOM [электронный ресурс]. URL: http://www.jetcom.ru/produc-tion/file-formats (дата обращения: 19.04.2016).
- Торстен Б., Меллер, Эмиль Райф, Атлас рентгенологических укладок. М.: Медицинская литература, 2009. 512 с.







