Для численного интегрирования системы дифференциальных уравнений и удобства анализа динамических процессов, происходящих в механизме, составлена компьютерная программа "Программа для моделирования функционирования лебедки, оснащенной ленточным фрикционом внутреннего типа" на языке Object Pascal в интегрированной среде программирования Borland Delphi 7.0. В тексте программы могут быть изменены любые конструктивные параметры как фрикциона новой конструкции. так и лебедки в целом.
Программа позволяет проводить компьютерные эксперименты с моделью лебедки. Компьютерный эксперимент заключается в наблюдении за состоянием механической системы в течении некоторого времени и получении временных зависимостей различных параметров механизма, в первую очередь, угловых скоростей ωD(t), ωR(t), ωV(t), ωB(t), ωT(t). По окончании расчета программа выводит на экран графики перечисленных зависимостей, а также записывает протабулированные функции в файлы [1].
Движение составных частей лебедки индуцируется движением тела D, имитирующим привод лебедки. В модели учитывается, что при возникновении нагрузки на лебедке двигатель снижает обороты (принят пропорциональный закон снижения):
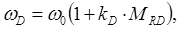 (1)
(1)
где ω0 – угловая скорость вращения вала на холостых оборотах;
kD – коэффициент пропорциональности;
MRD – момент, с которым тело R действует на тело D.
Момент MRD, как правило, принимает отрицательные значения, поэтому с приложением нагрузки частота вращения линейно снижается.
Вращение ведущей полумуфты R определяется моментом, действующим со стороны привода MRD, и моментом сил сцепления в фрикционном устройстве MVR. В соответствии с основным законом динамики вращательного движения можем записать следующее уравнение движения [2].
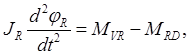 (2)
(2)
где φR – момент инерции и угловая координата ведущей полумуфты;
t – время.
Аналогичным образом записываются уравенния движения тел V, B и T:
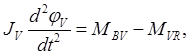 (3)
(3)
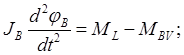 (4)
(4)
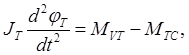 (5)
(5)
где φV, φB, φT – угловые координаты ведомой полумуфты, тросового барабана и ленточного тормоза;
MBV – момент вязкоупругого углового взаимодействия ведомой полумуфты и барабана;
ML – вращающий момент со стороны наматываемого троса;
MVT – момент сил сцепления, возникающих на поверхностях ленточного тормоза;
MTC – момент сил связи ленточного тормоза с корпусом лебедки.
Численное интегрирование системы (1–5) производится усовершенствованным методом Эйлера-Коши. Шаг интегрирования выбирается намного меньшим характерных времененных интервалов переходных процессов. В данном случае выбран шаг интегрирования Δt = 1·10–4 c.
Для компьютерных расчетов использовали следующие значения параметров:
ω0=3 об/с; kD=0,0005;
JR=0,5 кг·м2; JV=1,0 кг·м2; JB=10,0 кг·м2; JT=0,2 кг·м2;
CRD=500 Н·м/рад; βRD=25 Н·м·c/рад;
CBV=500 Н·м/рад; βBV=100 Н·м·c/рад;
CTC=500 Н·м/рад; βTC=200 Н·м·c/рад;
CVR=2000 Н·м/рад; βVR=250 Н·м·c/рад;
βVT=2000 Н·м·c/рад;
ωкр=2,5 рад/с;
kP=10–5 Па–1;
kL=50 Н·м·c/рад;
Pкр.ф.=1,0·105 Па; Pкр.ф.=0,5·105 Па.
Начальные условия были следующими:
ωD(t=0)=0, ωR(t=0)=0, ωV(t=0)=0, ωB(t=0)=0, ωT(t=0)=0;
φD(t=0)=0, φR(t=0)=0, φV(t=0)=0, φB(t=0)=0, φT(t=0)=0.
Компьютерный эксперимент проводили в течение 10 секунд модельного времени. При этом с механической системой производили три операции:
– выдерживали некоторое время для затухания переходных процессов связанных с раскруткой приводом D ведомой полумуфты R;
– включали сцепление муфты и выдерживали некоторое время для раскрутки барабана и выхода на установившийся режим трелевки;
– выключали муфту и включали тормоз, затем выдерживали некоторое время для затухания переходных процессов и полной остановки.
Включение и выключение муфты производили изменением давления PУ управляющего пневмоцилиндра, при этом временную зависимость PУ(t) в отдельные интервалы времени считали линейной:
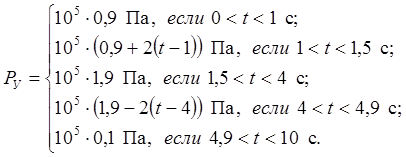 (6)
(6)
На рисунке 1 изображена зависимость PУ(t), а также временные зависимости угловых скоростей всех тел механизма.
Анализируя графики, можно прийти к выводу, что при включении и выключении фрикционной муфты происходят восемь типов процессов (отмечены римскими цифрами на рисунке 2.11).
На этапе I происходит раскрутка ведомой полумуфты вращающимся со скоростью ω0 приводом. При этом наблюдается резкий всплеск угловой скорости полумуфты ωR с последующим затуханием и выходом на установившееся значение. На этапе II происходит вращение ведомой полумуфты от привода с постоянной скоростью ω0, при этом фрикционная муфта находится в расцепленном состоянии. На этапе III управляющим пневмоци-

Рисунок 1 – Результаты компьютерного эксперимента
линдром начинают соединяться фрикционные поверхности муфты и муфта находится в режиме "буксование".При этом снижаются обороты привода ωD, а ведомая полумуфта раскручивается (увеличивается ωV), увлекая за собой барабан (ωВ). К началу этапа IV разность скоростей ωR–ωV становится достаточно малой, чтобы произошла смена режима трения с "буксования" на "сцепление". Фрикционные поверхности жестко сцепляются, при этом переходные процессы постепенно затухают и скорости ωD, ωR, ωV и ωB становятся одинаковыми. На протяжении этапа V муфта сцеплена и происходит трелевка бревна. Этап VI – отключение муфты: сначала происходит ослабление давления на фрикционной паре и довольно большое смещение одной поверхности относительно другой. Затем, когда разность скоростей поверхностей приобретет достаточную величину режим "сцепление" изменяется на "буксование". В режиме "буксования" происходит дальнейшее уменьшение давления PУ, и буксующие поверхности все более расцепляются. Скорости привода и ведущей полумуфты возвращаются к значению ω0, а скорости ведомой полумуфты и тросового барабана стремятся к нулю. На этапе VII включается ленточный тормоз, который очень быстро "зануляет" скорости ωV и ωB. На этапе VIII, как и на этапе II, лебедка находится в установившемся расцпеленном состоянии.
Благодаря высокой степени универсальности модель позволяет изучить влияние большого количества параметров фрикционного устройства, лебедки и процесса трелевки на эффективность функционирования механизма. Основными характеристиками лебедки, которые подлежат улучшению, являются время сцепления и время расцепления барабана с приводом, зависящие от параметров фрикционного устройства, а также плавность сцепления и расцепления, определяемая отсутствием резких или долгозатухающих всплесков на графиках ωi(t). Основной зависимостью для дальнейшего анализа является зависимость ωB(t), так как данная характеристика вращения тросового барабана определяет качество трелевки.
На рисунках 2–5 показаны зависимости угловой скорости барабана ωB(t) от нагрузки, коэффициента вязкого трения, мощности привода, коэффициента трения. Анализируя графики можно выбрать наиболее рациональные параметры фрикционного устройства.
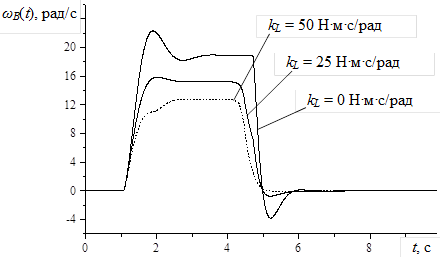
Рисунок 2 – Влияние нагрузки на тросе на угловую скорость тросового барабана ωB(t)
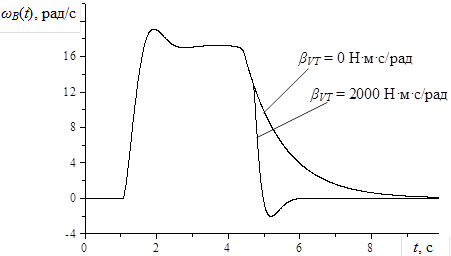
Рисунок 3 – Влияние трения в ленточном тормозе на угловую скорость тросового барабана ωB(t)

Рисунок 4 – Влияние коэффициента снижения оборотов привода на его угловую скорость ωD(t)
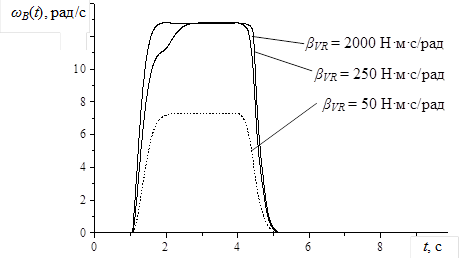
Рисунок 5 – Влияние коэффициента трения фрикционной муфты на угловую скорость тросового барабана ωB(t)
Библиографический список
1. Попиков, П. И. Повышение эффективности гидрофицированных машин при лесовосстановлении на вырубках [Текст] : [монография] / П. И. Попиков; Воронеж. гос. лесотехн. акад. - Воронеж, 2001. – 156 с. : ил. - ISBN 5-7994-0079-8.
2. Кондратьев Л. П. Исследование и совершенствование ленточных фрикционных устройств подъемно-транспортных машин [Текст] : монография / Л. П. Кондратьев, Н. И. Послухаев, П. И. Попиков ; Фед. агентство по образованиию, ГОУ ВПО «ВГЛТА». – Воронеж, 2009. – 264 с.







