На практике АРД-диаграмма (или шкала) обеспечивает пересчет амплитуды сигнала от какого-либо опорного уровня, например, донного сигнала, к сигналу от плоскодонного отражателя заданных размеров, находящегося на определенной глубине, что позволяет настроить дефектоскоп на браковочный, поисковый и др. уровни чувствительности. Поскольку вручную на бумаге составить диаграмму крайне затратно по времени, а специально созданные для этого программы находятся в платном доступе, актуальным решением проблемы является построение АРД-диаграммы в программе Mathcad.
Ключевые слова: АРД-диаграмма, уравнение акустического тракта, Mathcad
Для расчета амплитуды эхо-сигнала от дефекта в широком диапазоне расстояний и размеров дефектов применяются АРД-диаграммы — семейство кривых, устанавливающих зависимость между амплитудой эхо-сигнала от дискового отражателя, ориентированного перпендикулярно акустической оси ПЭП и отражающего до 100 % падающей на него ультразвуковой энергии, расстоянием от излучателя до отражателя и размером — площадью или диаметром отражателя. Отложив по горизонтальной оси расстояние между отражателем (дефектом) и излучателем (ПЭП), отнесенное к расстоянию от преобразователя до дефекта, получим группу кривых, показывающих зависимость от расстояния до дефекта. Каждой кривой соответствует определенный размер (диаметр) отражателя, отнесенный к диаметру пьезоэлемента.
Как пример в данной работе будет рассчитана АРД-диаграмма для бериллиевого слитка длиной и шириной 100 мм, скорость продольных волн в бериллии – 
=12550 
.
Контроль будет производиться прямым совмещенным преобразователем с частотой 
, радиус преобразователя a = 6 мм. Коэффициент затухания звука на заданной частоте равен 6 Дб/м.
Математически кривые задаются с помощью уравнений акустического тракта, при экспериментах модели дефектов заменяются искусственными отражателями, типовые модели и уравнения приведены на рисунке 1.
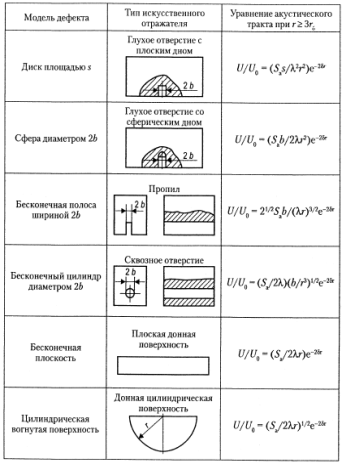
Рис. 1. Формулы акустического тракта прямого совмещенного ПЭП с круглым пьезоэлементом
Где: r — расстояние от излучателя до дефекта; 
– расстояние от излучателя до конца ближней зоны; 
– площадь излучателя; s – площадь отражателя; λ – длина волны; δ – коэффициент затухания; U – амплитуда зондирующего сигнала; 
– амплитуда сигнала, отраженного дефектом и принятого преобразователем.
Для начала необходимо задать ряд размеров выявляемых дефектов (d1-d8) и диаметр пьезоэлектрического преобразователя d.
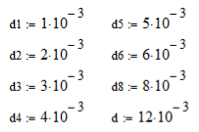
Зададим частоту преобразователя — f; скорость продольных волн — c1; расстояние до дефекта — r; длину волны — λ; коэффициент затухания — δ.
Следует учесть, что формулы акустического тракта справедливы при условии, что расстояние до дефекта больше чем размер трёх ближних зон (
).
Рассчитаем величину ближней зоны:
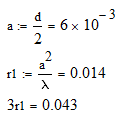
Используя уравнение акустического тракта диска с площадью s, для дефектов 1, 2, 3, 4, 5, 6 и 8 мм соответственно, и бесконечной плоскости, для донного сигнала, зададим семейство кривых.
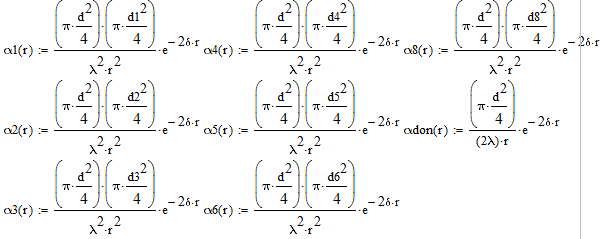
Произведем построение АРД-диаграммы (рис. 2.), по оси ординат отложено отношение амплитуд зондирующего сигнала к сигналу отраженному от дефекта 
в отрицательных децибелах, по оси абсцисс расстояние до дефекта в метрах.
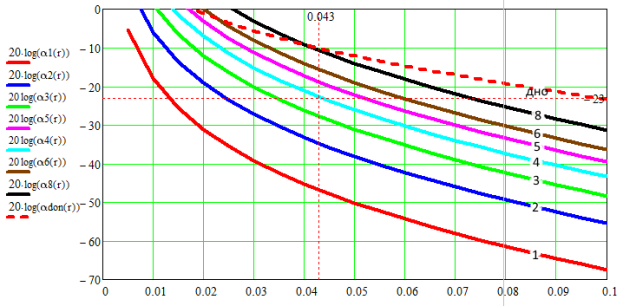
Рис. 2. АРД-диаграмма
Исходя из данной АРД-диаграммы легко заметить, что минимальный выявляемый размер дефекта при прозвучивании изделия на расстоянии 100 мм равен 2 мм, так как разница в амплитуде между данным отражателем и донной поверхностью не превышает 40 дБ, т. е. на 6 дБ меньше, чем разница между амплитудой донного сигнала и уровнем шумов. Таким образом можно утверждать, что сигнал от дискового отражателя диаметром 2 мм, находящегося на максимальном расстоянии при этом направлении прозвучивания будет отчетливо виден над уровнем шумов (превышать его на 6 дБ). Расчеты справедливы при нахождении дефекта на расстоянии 43 мм от преобразователя.
В данной работе был описан принцип построения АРД-диаграмм в программе Mathcad, а именно представлен расчет акустического тракта для плоскодонного отверстия в бериллиевом слитке толщиной 100 мм. По аналогичному принципу возможен расчет диаграммы для любого металла в котором известен коэффициент затухания и скорость продольных волн.
Литература:
- Очков В. Ф. MathCAD 14 для студентов, инженеров и конструкторов. — СПб.: БХВ-Петербург, 2007. — 368с.
- Кретов Е. Ф Ультразвуковая дефектоскопия в энергомашиностроении. — 3 изд. — М.: СВЕН, 2007. — 296 с.
- Шушкевич Г. Ч, Шушкевич С. В. Компьютерные технологии в математике. Система Mathcad 14. В 2 частях. Часть 2. Издательство Гревцова, 2012. – 256 с.
