Представление знаний о процессах с помощью многократных цепей Маркова



Ключевые слова: process mining, АЦП, цепи Маркова

В XXI веке, веке информации и информационных технологий, происходит постоянное генерирование данных. Согласно исследованиям, за последние 10 минут, в мире было сгенерировано столько же данных, сколько за всё время существования человечества до 2003 года.

Основная часть генерируемых данных — это данные, о событиях, произошедших или запланированных. Главные источники подобных событийных данных — это информационные системы, базы данных в различных областях. К таковым можно отнести: образование, туризм, страхование, банковские данные, медицина и т. д.

Значительная часть подобной информации хранится в журналах событий, в логах, в базах данных. Как правило, это огромное количество строк, которые как раз и содержат информацию о данных, произошедших в определенном событии.

Process mining — это как раз то, что даёт ответ на вопрос «Что же делать со всеми этими данными», а именно, как их обрабатывать, исследовать, и какие делать выводы на их основе.

Целью данной работы является исследование и представление знаний о простом процессе; во время исследования найти в нем все составляющие большого процесса. Изучение данного вопроса будет происходить с помощью многократных цепей Маркова.

1. Process Mining.

Process Mining находитсянастыкетакихобластейзнаний, как: Formal Modeling & Verification, Business Process Management, Data mining. Корни теорий и приложений формального моделирования, в каком-то смысле идут от логистики. С другой стороны сейчас PM прежде всего включает в себя методы из Business Process Management. Это, в каком — то смысле прикладная, связанная с коммерцией область, управление бизнес процессами. Под бизнес процессами понимается не как различные коммерческие, а как процессы в прикладной области. Data Mining — это то, откуда были взяты основные методики, идеи. То есть мы анализируем данные (Data Mining), прикладные процессы (Business Process Management), используя при этом, в том числе, методы формального моделирования (Formal Modeling & Verification). Применение Process mining для анализа поведения пользователей информационных систем зависит прежде всего от наличия подходящих логов и от разумной постановки вопроса.

1.1 Цепи Маркова иАЦП.

Теория вероятностей включает три раздела: случайные события, случайные величины, случайные процессы

Цепью Маркова называют такую последовательность случайных событий, в которой вероятность каждого события зависит только от состояния, в котором процесс находится в текущий момент и не зависит от более ранних состояний.

Матрицей переходных вероятностей P = {pij}, характеризующей вероятность перехода процесса с текущим состоянием si в следующее состояние sj, при этом сумма вероятностей переходов из одного состояния равна 1:

∑j=1…n pij = 1

Процесс преобразования аналого-цифровых преобразователей (АЦП) рассматривается как случайны процесс с дискретным временем и конечным числом состояний. При анализе процесса преобразования используется аппарат цепей Маркова. Для полноты и удобства анализа АЦП рассматриваются как многоуровневые структуры. Анализируются особенности преобразования на различных уровнях

Анализ разработанных структур, учитывающих кодовые эквиваленты предыдущих значений входного сигнала, показал, что в основном алгоритмы их работы на втором уровне сводятся к определению поддиапазона нахождения сигнала с последующим определением значения сигнала в найденном поддиапазоне. Шаг квантования при этом изменяется по величине. Следовательно, процесс формирования текущего образцового уровня g может быть записан в виде

q [i]= φ(ω, x [i-1], g [i-1], g [i-2], g [i-3]), (3.6)

где x [i-1] — значение соответствующего x [i-1], с наложенным на него шумом.

Предполагаем шум нормальным, поэтому можем использовать интеграл вероятности.

Интеграл вероятности вычисляется по формуле:

2.1 Спецификация данных.

Обобщенная информация приведена в сводной таблице информации о требуемом формате представления данных.

Таблица 1

Требуемые форматы данных

Процедура	Описание
Float alf, bet, gam, del	ответ схемы сравнения эталона и входного сигнала
Void printny(nys *ny, int jny)	печать таблицы номер состояния
Pms pmt [200]	переходная матрица — из состояния в состояние при ответе схемы сравнения
Void printpm(pms *pm, int jny);	печать переходной матрицы
Void signal(float j, int d, sost q);	вспомогательный сигнал для определения всех переходов из состояния в состояние
Void fpm1(nys *ny, int d,jny, float jm, real *pm1);	формирование матрицы переходных вероятностей
Void printpm1(real *pm1, int jny);	печать матрицы переходных вероятностей

2.2 Формирование состояний вматрице.

− Берем первое состояние, инициализируем, присваивая ему первый номер;

− Когда подаётся сигнал больше, переходим в другое состояние, учитывая, есть ли это состояние в матрице, если есть, тогда берем его номер, если нет, тогда его вводим и присваиваем следующий номер;

− Далее проделываем по аналогии пункта 2, вводя все состояния.

Получаем:

Таблица номер-состояние jny=63

2.3 Формирование переходной матрицы.

− На полученные состояния могут подаваться сигналы, α, β;

− Есть 1 состояние и подаётся сигнал α, т. е. сигнал идет выше, и смотрим в какое переходит состояние;

− Таким образом создаётся матрица переходов для всех состояний.

Переходная матрица.

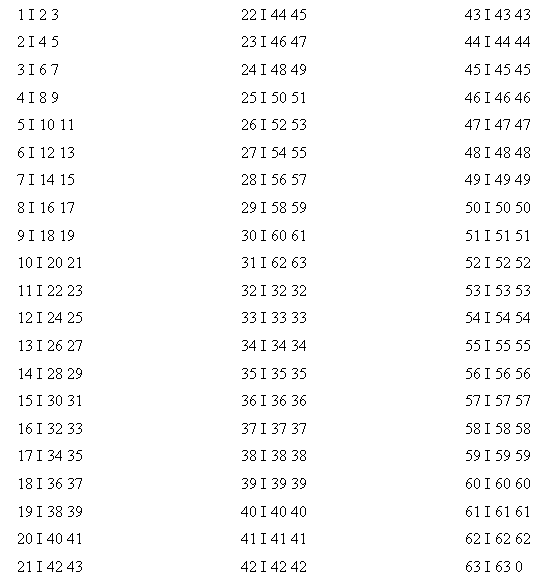
2.4 Формирование матрицы переходных вероятностей.

При сигнале и наложенном на него нормально распределенным шумом, мы подсчитываем для каждого перехода состояний вероятность точного сигнала

− Находясь в 1 состояние при сигнале α перехожу в состояние 3 с определенной вероятностью;

− Далее заполняем матрицу вероятностей для каждого перехода.

Получаем:

Матрица переходных вероятностей

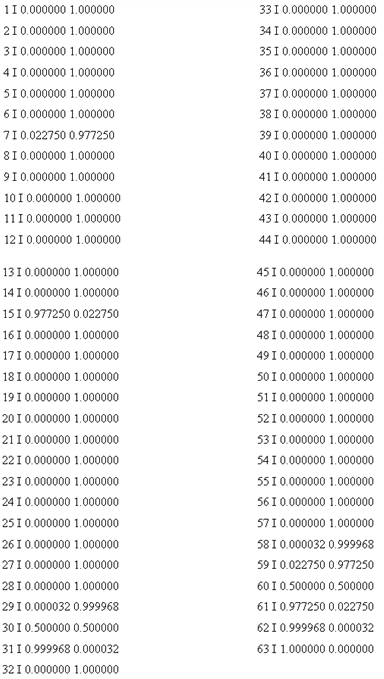
2.5 Графики колебания значений при увеличении σ сшагом 0,1.

Графики колебания значений при увеличении σ с шагом 0,1 представлены на рисунках 1, 2, 3, 4, 5, 6, 7, 8.

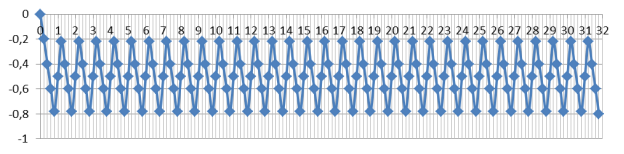
рис. 1. График значений при σ₌0,1

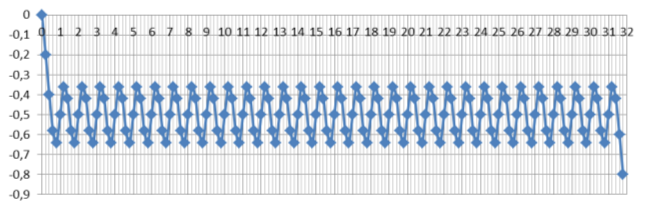
рис. 2. График значений при σ₌0,2

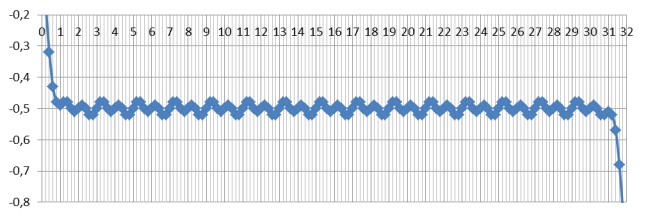
рис. 3. График значений при σ₌0,3

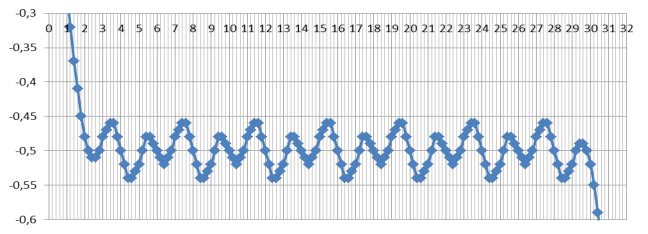
рис. 4. График значений при σ₌0,4

рис. 5. График значений при σ₌0,5

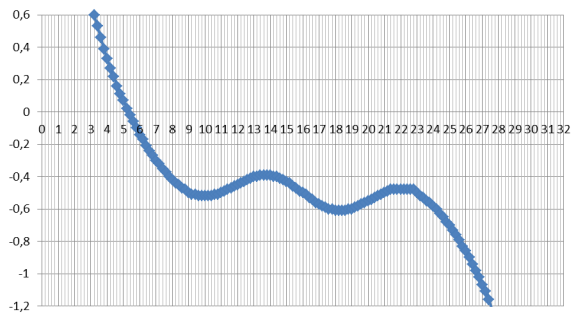
рис. 6. График значений при σ₌0,6

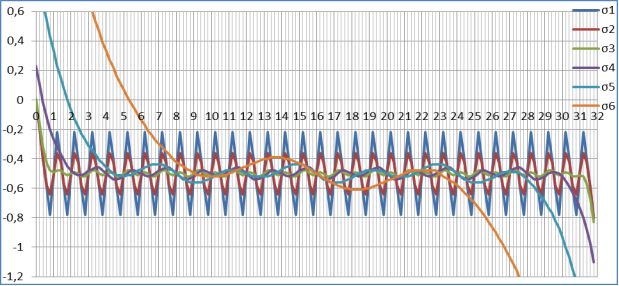
рис. 7. График значений при σ₌0,7

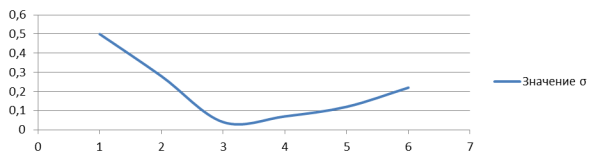
рис. 8. График изменения значений амплитуд, с изменением значений σ

Заключение.

На первом уровне осуществляется слежение за изменяющимся сигналом с переменным шагом квантования. Поэтому необходимо найти правила увеличения и уменьшения величины шага квантования, позволяющие уменьшить погрешность и число состояний АЦП. Проведенные исследования показали перспективность АЦП, в которых величина кодового эквивалента образцового уровня кратна величине шага квантования.

На втором уровне осуществляется преобразование постоянного сигнала, возможное при наличии помех и одиночных сбоев. Для борьбы с одиночными сбоями можно использовать алгоритмы преобразования с повышенной достоверностью. Были разработаны алгоритмы, в основе которых лежит допущение о том, что шаг квантования можно уменьшать при условии чередования ответов схемы сравнения. Также были разработаны алгоритмы, осуществляющие поиск поддиапазона расположения сигнала, а затем преобразования самого сигнала. Эти алгоритмы учитывают состояние процесса первого уровня.

На третьем уровне для борьбы с помехами можно использовать либо классическое усреднение, либо последовательный анализ. Таким образом, использование цепей Маркова позволило с единых позиций описать процесс преобразования существующих АЦП.

Так как число состояний цепи Маркова, описывающей процесс преобразования, сильно зависит от вида входного сигнала и от разрядности АЦП, то представляется целесообразным использовать аппарат цепей Маркова. При этом разрядность АЦП можно выбирать в пределах 4–7 разрядов, а в качестве входного сигнала можно использовать сигнал, описываемый однократной или двукратной цепью Маркова.

Таким образом, приведенные результаты показывают, что использование Марковских цепей позволяет однотипно, точно и быстро проводить вероятностный анализ различных АЦП.

Литература:

1. IEEE CIS Task Force on Process Mining. Process Mining Manifesto. LNBIP 99, pp. 169–194. Springer, 2012. DOI: 10.1007/978–3–642–28108–2_19
2. Wil van der Aalst. Process Mining: Discovery, Conformance and Enhancement of Business Processes. Springer, 2011.
3. Alexey Mitsyuk, Anna Kalenkova, Sergey A. Shershakov, van der Aalst W. Using process mining for the analysis of an e-trade system: A case study // Бизнес-информатика. 2014. Vol. 29. №. 3. P. 15–27.
4. Suriadi et al. Understanding Process Behaviours in a Large Insurance Company in Australia: A Case Study. In Advanced Information Systems Engineering — LNCS, pp. 449–464. Springer, Valencia, Spain, 2013.
5. Научно-учебная лаборатория процессно-ориентированных информационных систем (ПОИС). – http://pais.hse.ru/
6. Process Mining Workbench. – http://www.promtools.org/
7. Андросенко О. С., Девятченко Л. Д., Маяченко Е. П. Постановка задач Марковских процессов в формате программы WinQSB // Математика. Приложение математики в экономических, технических и педагогических исследованиях: Сб. науч. тр./ Под ред. М. В. Бушмановой. Магнитогорск: ГОУ ВПО «МГТУ», 2006. С. 3–13.
8. Вентцель Е. С., Овчаров Л. А. Прикладные задачи теории вероятностей. — М.: Радио и связь, 1983. — 416 с., ил. 6. Воеводин В. В., Кузнецов Ю. А. Матрицы и вычисл.
9. Тихонов В. И., Миронов М. А. Марковские процессы.
10. А. с. 780184 (СССР). Следящий аналого-цифровой преобразователь. / В. Э. Балтрашевич — Опубл. В Б. И., 1980
11. А. с. 797064 (СССР). Следящий аналого-цифровой преобразователь. / В. Э. Балтрашевич — Опубл. В Б. И., 1981, № 2.
12. Process Mining — https://ru.wikipedia.org/wiki/Process_mining
13. Использование Process Mining — https://habrahabr.ru/post/244879/