We constructed the asymptotic expansion bisingular Cauchy problem for a parabolic equation, in the case, when the corresponding unpertrurbed equation will have the pole of the second order in beginning of the time. Asymptotic expansion of the solution constructed by the generalized method of boundary functions. It is given the estimate of the reminder term of the asymptotical expansion of the solution..
Key words: asymptotic, singularity, equation of parabolic type, besingularly problem, pole, generalized method of boundary functions
- Постановка задачи. Исследуем задачу Коши на бесконечной прямой
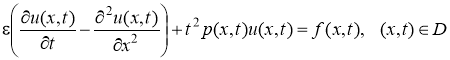 , (1)
, (1)
u(x,0)=(x), –<x<+, (2)
где — малый положительный параметр, p(x,t)>0 (x,t)![]() ,
, ![]() , f(x,0)0, D={(x,t)| –<x<+, 0t}, C(R), u(x,t) — искомая функция.
, f(x,0)0, D={(x,t)| –<x<+, 0t}, C(R), u(x,t) — искомая функция.
Очевидно, что задача (1)-(2) является бисингулярной. Так как невозмущенная задача (=0) имеет решение, которое имеет полюс второго порячдка в точке t=0. Отметим, что в [1] рассмотрен случай, когда невозмущунное уравнение имеет полюс первого порядка при t=0
- Построение асимптотики решения обобщенным методом погранфункций К.Алымкулова [1]- [4]. Решениезадачи (1)-(2) будем искать в виде
u(x,t)=V(x,t)+W(x,), (3)
где 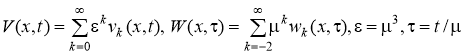 .
.
Для начала уравнение (1) запишем в виде
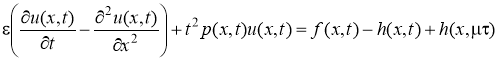 , (4)
, (4)
как заметили, мы здесь ввели асимптотический ряд
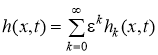 .
.
После подстановки соотношения (3) в уравнение (4) получаем:
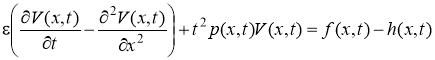 , (5)
, (5)
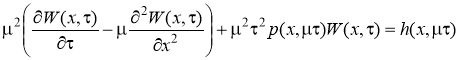 . (6)
. (6)
Начальное условие для пограничной функции W(x,) примет вид
W(x,0)=(х)–V(x,0). (7)
Из равенства (5) имеем:
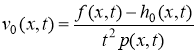 ,
, 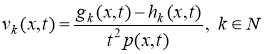 .
.
где 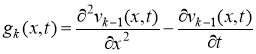 .
.
Пусть 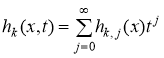 и h0,0(x)=f(x,0), h0,1(x)=
и h0,0(x)=f(x,0), h0,1(x)=![]() , hk,0(x)=gk(x,0), hk,1(x)=
, hk,0(x)=gk(x,0), hk,1(x)=![]() . Тогда
. Тогда ![]() Остальные функций hk,j(x) подберем так, чтобы выполнялись условия
Остальные функций hk,j(x) подберем так, чтобы выполнялись условия
![]() при +, –<x<+.
при +, –<x<+.
Теперь перейдем к определению членов ряда
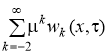 . Равенство (6) запишем в виде:
. Равенство (6) запишем в виде:
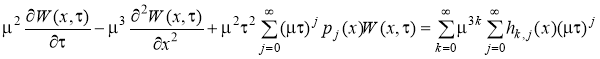 .
.
Отсюда имеем:
![]() (8)
(8)
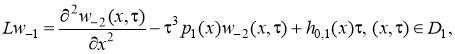 (9)
(9)
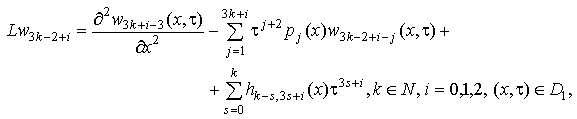 (10)
(10)
где D1={(x,)| –<x<+, 0<<+}.
Из (7) имеем
w0(x,0)=(х)–v0(x,0), w3k(x,0)=–vk(x,0), wm(x,0)=0, m3kkN. (11)
Докажем вспомогательные теоремы.
Теорема 1. Пусть ![]() , z0(x)C(R), a(x)>0. Тогда задача
, z0(x)C(R), a(x)>0. Тогда задача
имеет единственное решение ![]() .
.
Доказательство. Интегрируя дифференциальное уравнение (12) с начальным условием, получаем единственное решение задачи (12):
![]() .
.
Заметим, что если F(x,)=O(n), +, n — const, то z(x,)=O(n–2), +. Из теоремы 1 следует существование и единственность решений задач (8)-(11).
Теорема 2. Пусть 0<a(x)C(R) и функции Fj(x,)C(![]() ) разлагаются в асимптотические ряды
) разлагаются в асимптотические ряды
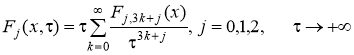 , –<x<+.
, –<x<+.
Тогда в области D1, существуют решения уравнений
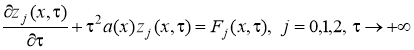 , (13)
, (13)
которые разлагаются в ряды
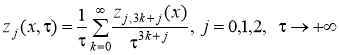 . (14)
. (14)
Доказательство. Заметим, что дифференцируемость асимптотических рядов (14) вытекает непосредственно из (13). Разложение ищем в виде (14), где
Теорема 3. Пусть для функций 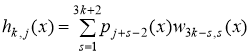 , k=0,1,…, j=2,3,… Тогда при + справедливы асимптотические разложения
, k=0,1,…, j=2,3,… Тогда при + справедливы асимптотические разложения
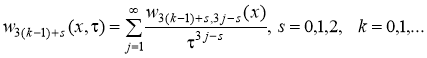
Доказательство. Последовательно применяя теорему 2 для уравнений (8) и (9), получаем
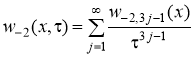 ,
, 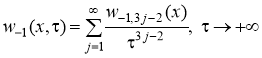 , (15)
, (15)
где 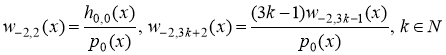 .
.
Теперь в (10) мы выбираем функции ![]() так, чтобы максимальная степень разложения по правых частей равенств (10) не превышало 2 когда +. Из (10) при k=0 и i=2 имеем:
так, чтобы максимальная степень разложения по правых частей равенств (10) не превышало 2 когда +. Из (10) при k=0 и i=2 имеем:
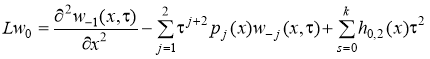 , (16)
, (16)
Если h0,2(x)=p1(x)w–1,1(x)+p2(x)w–2,2(x), то применяя асимптотические разложения (15) и теорему 2 для уравнения (16), получаем:
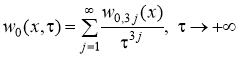 .
.
Аналогично доказываются и остальные случаи.
Таким образом, нами определены все члены асимптотического решения (3). Перейдем теперь к оценке остаточной функции.
Оценка остаточного члена. Пусть ![]() ,
, 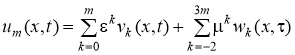 . Тогда для остаточной функции Rm(x,t) получим задачу
. Тогда для остаточной функции Rm(x,t) получим задачу
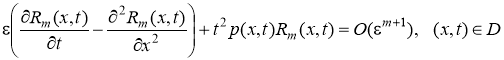 , (17)
, (17)
Rm(x,0)=O(m+1), –<x<+, 0. (18)
К задаче (17)-(18) применяем преобразование Rm(x,t)=(1+t)rm(x,t), тогда относительно функции rm(x,t) получаем задачу
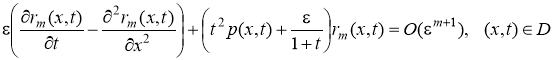 ,
,
rm(x,0)=O(m+1), –<x<+, 0.
Из принципа максимума [5], следует справедливость оценки:
rm(x,t)=O(m), 0, ![]() .
.
Отсюда следует, что Rm(x,t)=O(m), 0, ![]() .
.
Следовательно, справедлива
Теорема 4. Для решения задачи (1)-(2) при 0 справедливо асимптотическое разложение (3).
Пример. Рассмотрим задачу
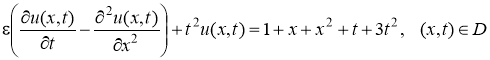 , (19)
, (19)
u(x,0)=x, –<x<+. (20)
Асимптотическое разложение решения задачи (19)-(20) ищем в виде
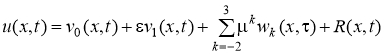 , (21)
, (21)
где R(x,t) — остаточная функция.
Учитывая равенство (5) получаем:
v0(x,t)=3, vk(x,t)=0, при h0(x,t)=1+x+x2+t, hk(x,t)=0, kN.
Задачи (8)-(11) примут вид:
![]() , (22)
, (22)
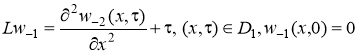 , (23)
, (23)
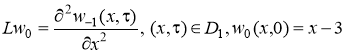 , (24)
, (24)
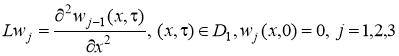 . (25)
. (25)
Решения задач (22)-(25) представимы в виде, соответственно
![]() ,
,
![]() ,
,
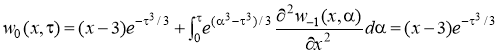 ,
,
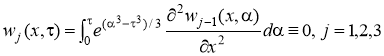 .
.
Отметим, что при +, хR справедливы соотношения
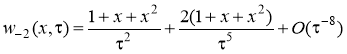 ,
, ![]() .
.
Задача для остаточной функции имеет вид:
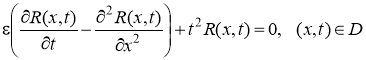 ,
,
R(x,0)=0, –<x<+.
Отсюда R(x,t)0. Следовательно,
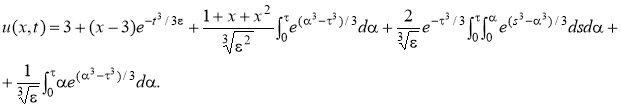
Заключение. Нами доказано применимость обобщенного метода пограничных функций для построения равномерного асимптотического разложения решения бисингулярной задачи на бесконечной прямой с квадратичным ростом сингулярности по времени, с любой степенью точности по малому параметру. Благодаря данному методу нам удалось получить точную оценку для остаточной функции.
Литература:
- Алымкулов К., Турсунов Д. А., Кожобеков К. Г. Обобщенный метод пограничных функций для бисингулярной задачи на бесконечной прямой // Приволжский научный вестник № 8 (60). 2016. — С. 8–12.
- Alymkulov, K. Extension of boundary layer function method for singularly perturbed differential equation of Prandtle-Tichonov and Lighthill types // Reports of the third congress of the world mathematical society of Turkic countries, Almaty, June July, 2009. –P 256–259.
- Alymkulov, K. Analog of Method of Boundary Layer Function for the Solution of the Lighthill’s Model Equation with the regular Singular Point // AmericanJ.Math. & Statistics, 2013, v. 3, n.1. — P. 53–61.
- Алымкулов К., Турсунов Д. А. Об одном методе построения асимптотических разложений решений бисингулярно возмущенных задач // Известия вузов. Математика. 2016, № 12, — С. 3–11.
- Friedman A. Partial differential equation of parabolic type. Prentice-hall, inc.glewood Cliffs, N.J. 1964.







